В этой статье мы объясним, что такое постоянная функция и каково ее графическое представление. Кроме того, вы сможете увидеть несколько примеров функций-констант и все характеристики функций этого типа. И, наконец, вы сможете тренироваться, решая упражнения постоянных функций.
Что такое постоянная функция?
Постоянная функция — это та функция, которая всегда принимает один и тот же образ для любого значения независимой переменной (x) , т. е. постоянная функция имеет вид f(x)=k , где k — любое действительное число.
![]()
Графическим представлением постоянной функции является горизонтальная линия.
Например, все следующие функции являются константами:
![]()
Графическое представление постоянной функции
Познакомившись с понятием постоянной функции, мы увидим, как представить постоянную функцию на графике.
Построить график постоянной функции довольно просто: достаточно провести горизонтальную линию по значению функции (k).
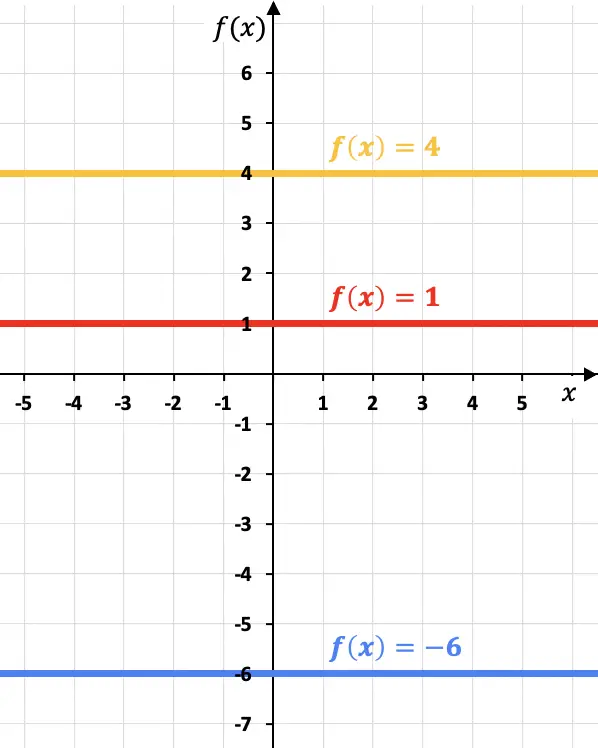
Посмотрите на следующие примеры, в которых мы представили на графике три разные постоянные функции:

Обратите внимание, что каждая постоянная функция параллельна оси X.
С другой стороны, вы должны иметь в виду, что вертикальная линия не является постоянной функцией. Фактически, вертикальная линия даже не является функцией, поскольку по определению функция может иметь только одно изображение для каждого значения x.
Характеристики постоянной функции
Далее мы проанализируем свойства постоянной функции. Рассмотрим постоянную функцию любого значения:
![]()
- Областью определения постоянной функции являются все действительные числа:
![]()
- Путь или диапазон постоянной функции — это только значение константы:
![]()
- Это непрерывная и четная функция, поскольку функция всегда принимает одно и то же значение:
![]()
- Постоянная функция не является ни возрастающей, ни убывающей, это тип функции, которая всегда имеет нулевой наклон:
![]()
- Он всегда пересекает ось OY в точке (0,k).
![]()
- Любая постоянная функция является полиномом нулевой степени.
- Ага
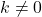
вместо этого постоянная функция не имеет корня, если
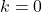
все действительные числа являются корнями постоянной функции.
- Предел постоянной функции при приближении x к плюс бесконечности или минус бесконечности равен значению константы:
![]()
![]()
- Производная постоянной функции всегда равна нулю:
![]()
Фактически, определение постоянной функции также можно дать, исходя из понятия производной: функция является постоянной, если ее производная равна нулю во всей ее области определения.
- Интеграл от постоянной функции представляет собой линейную (или аффинную) функцию:
![]()
➤ См.: Что такое линейная функция?
Постоянная функция на интервале
Мы видели, что функция постоянна, однако функция может быть постоянной только в определенном интервале своей области определения.
Чтобы понять эту концепцию, вам необходимо знать, какие функции определяются частями, поэтому, прежде чем продолжить, мы рекомендуем взглянуть на следующее объяснение:
➤ См.: Что такое кусочная функция?
Как только вы узнаете, что это за типы функций, посмотрите на функцию, определенную в частях, показанных ниже:

Как видно из графика, функция не является постоянной для всех чисел в своей области определения. Но она постоянна на интервале [-2,4), поэтому является постоянной функцией только на одном интервале.
Исправлены проблемы с постоянной функцией
Упражнение 1
Определите, какие из следующих функций являются константами:
![]()
Первая функция,
![]()
, является постоянной функцией, поскольку она всегда равна 4, какое бы значение ни принимала переменная x.
Вторая функция,
![]()
, не является постоянной функцией, поскольку значение функции меняется в зависимости от значения x. Это аффинная функция.
Третья функция,
![]()
, всегда равна 0 для любого значения x, поэтому это действительно постоянная функция.
Четвертая функция,
![]()
, не является постоянной функцией, поскольку она меняется в зависимости от значения x. Это линейная функция.
Упражнение 2
Найдите постоянную функцию, проходящую через точку (0.6).
Алгебраически формула постоянной функции всегда имеет один и тот же вид:
![]()
А графически постоянная функция всегда представляет собой горизонтальную линию, следовательно, координаты постоянной функции всегда равны и имеют значение.
![]()
Поскольку точка, через которую проходит функция, имеет координату y=6, постоянная функция, которую мы ищем в этой задаче, должна быть:
![]()
Упражнение 3
Постройте следующие постоянные функции на одном графике:
![]()
Чтобы представить каждую постоянную функцию, просто нарисуйте прямую горизонтальную линию на высоте каждой константы: