На этой странице вы найдете формулы для всех уравнений плана и способы их расчета. Вы также узнаете, как найти уравнение любой плоскости с вектором нормали. Кроме того, вы сможете посмотреть примеры и потренироваться с решением уравнений плана.
Что такое уравнение плоскости?
В аналитической геометрии уравнение плоскости — это уравнение, позволяющее математически выразить любую плоскость. Итак, чтобы найти уравнение плоскости, нужна всего лишь точка и два линейно независимых вектора, принадлежащих этой плоскости.
Прежде чем продолжить объяснение уравнений плоскости, важно понять, что такое плоскость (геометрия) , потому что в противном случае будут вещи, которые вы не поймете. Если вам не совсем понятно, вы можете проверить это по этой ссылке, где мы собрали все, что вам нужно знать о плане.
Каковы уравнения плана?
Как мы видели в определении уравнения плоскости, любую точку плоской плоскости можно выразить как линейную комбинацию 1 точки и 2 векторов.

Однако необходимым условием соответствия уравнения плоскости является то, что два вектора плоскости обладают линейной независимостью, то есть два вектора не могут быть параллельны друг другу.
Таким образом, всеми типами уравнений плоскости являются: векторное уравнение , параметрические уравнения , неявное (или общее) уравнение и каноническое (или сегментное) уравнение плоскости.
Затем мы подробно увидим объяснение и формулы всех уравнений плана.
Векторное уравнение плоскости
Рассмотрим точку и два направляющих вектора плоскости:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Формула векторного уравнения плоскости :
![]()
Или эквивалент:
![]()
Золото
![]()
И
![]()
два скаляра, то есть два действительных числа.
Параметрические уравнения плоскости
Параметрическое уравнение плоскости можно определить из ее векторного уравнения. Ниже вы можете увидеть демо.
Пусть векторное уравнение любой плоскости имеет вид:
![]()
Оперируем и сначала осуществляем произведения векторов на скаляры:
![]()
Далее добавляем компоненты:
![]()
И, наконец, получим параметрические уравнения плана, усвоив координаты, соответствующие каждой переменной в отдельности:
![]()
Золото:
-
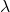
И
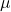
два скаляра, то есть два действительных числа.
-
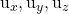
являются компонентами одного из двух направляющих векторов плана
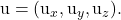
-
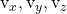
являются компонентами другого направляющего вектора плана
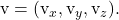
Неявное или общее уравнение плоскости
Рассмотрим точку и два направляющих вектора плоскости:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
Неявное, общее или декартово уравнение плоскости получается путем решения следующего определителя и присвоения результата, равного 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Таким образом, неявное или общее уравнение полученного плана будет следующим:
![]()
Этот тип уравнения плоскости также называют декартовым уравнением плоскости.
Каноническое или сегментное уравнение плоскости
Формула канонического или сегментного уравнения плоскости имеет следующий вид:
![]()
Золото:
-

— это точка пересечения плоскости и оси X.
-

— это точка пересечения плоскости и оси Y.
-

Здесь плоскость пересекает ось Z.
Каноническое уравнение (или сегментное уравнение) плоскости также можно получить из ее общего уравнения:
![]()
Сначала решаем коэффициент D из уравнения:
![]()
Затем разделим все уравнение плана на значение параметра D, изменившего знак:
![]()
![]()
И, используя свойства дробей, приходим к следующему выражению:
![]()
Поэтому мы выводим из этого выражения формулы, позволяющие непосредственно вычислять члены канонического или сегментного уравнения плоскости:
![]()
следовательно, чтобы можно было составить этот вариант уравнений плана, коэффициенты А, В и С должны быть отличны от нуля, что позволяет избежать неопределенности дробей.
Как вычислить уравнение плоскости по вектору нормали
Очень типичная задача в уравнениях плоскости — найти, как выглядит уравнение данной плоскости с учетом точки и ее нормального (или перпендикулярного) вектора. Итак, давайте посмотрим, как это работает.
Но прежде всего необходимо знать, что компоненты X, Y, Z вектора нормали к плоскости совпадают соответственно с коэффициентами A, B, C неявного (или общего) уравнения этой плоскости.
![]()
Золото
![]()
вектор, ортогональный плоскости
![]()
Как только мы узнаем предыдущее соотношение, давайте посмотрим пример решения такого типа задач с уравнением плоскости:
- Определите неявное или общее уравнение плоскости, проходящей через точку.
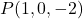
и один из его нормальных векторов есть
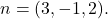
Формула неявного, общего или декартова уравнения плоскости:
![]()
Таким образом, из вектора нормали мы можем найти коэффициенты A, B и C, поскольку они эквивалентны компонентам его вектора нормали:
![]()
Пока нам нужно найти только параметр D. Для этого подставим в уравнение координаты точки, принадлежащей плоскости:
![]()
![]()
![]()
![]()
![]()
Таким образом, неявное или общее уравнение плана таково:
![]()
Решенные задачи с плоскими уравнениями
Упражнение 1
Определить векторное уравнение плоскости, содержащей вектор
![]()
и проходит через следующие два пункта:
![]()
И
![]()
Чтобы узнать уравнение плоскости, вам нужна точка и два вектора, и в этом случае у нас есть только один вектор, поэтому мы должны найти другой направляющий вектор плоскости. Для этого мы можем вычислить вектор, который определяет две точки плоскости:
![]()
Теперь, когда мы уже знаем два направляющих вектора плоскости и точки, поэтому воспользуемся формулой векторного уравнения плоскости:
![]()
И подставим в уравнение два вектора и одну из двух точек плоскости:
![]()
Упражнение 2
Найдите параметрические уравнения плоскости, содержащей следующие три точки:
![]()
Чтобы найти параметрические уравнения плоскости, нам нужно найти два линейно независимых вектора, которые соединяются в плоскости. И для этого мы можем вычислить два вектора, которые определяются тремя точками:
![]()
![]()
Координаты двух найденных векторов не пропорциональны, поэтому линейно независимы друг от друга.
Теперь, когда мы уже знаем два направляющих вектора и точку на плоскости, применим формулу параметрического уравнения плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
И подставляем в уравнение два вектора и одну из трёх точек плоскости:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f57edaf8a85108cffb796470ffca8484_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4cab5ddc074bd7df6849d71854207cf5_l3.png)
Упражнение 3
Найдите неявное или общее уравнение плоскости, проходящей через точку.
![]()
и содержит векторы
![]()
И
![]()
Чтобы вычислить общее или неявное уравнение плоскости, необходимо решить следующий определитель, образованный двумя векторами, тремя переменными и координатами точки:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
Итак, подставляем векторы и точку в формулу:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
А теперь решаем определитель матрицы 3×3 выбранным вами методом:
![]()
Наконец, выполняем операции и группируем подобные члены:
![]()
![]()
![]()
Таким образом, неявное или общее уравнение плана таково:
![]()
Упражнение 4
Определите, является ли точка
![]()
принадлежит следующему плану:
![]()
Чтобы точка находилась в плоскости, необходимо проверить ее уравнение. Поэтому нам нужно подставить декартовы координаты точки в уравнение плоскости и проверить, выполняется ли уравнение:
![]()
![]()
![]()
![]()
![]()
Точка не подчиняется уравнению плоскости, поэтому она не является частью этой плоскости.
Упражнение 5
Найдите сегментное уравнение плоскости, общее (или неявное) уравнение которого имеет вид:
![]()
Сначала удалим независимый член из уравнения:
![]()
Затем разделим все уравнение плана на значение коэффициента D, изменившего знак:
![]()
![]()
И, используя свойства дробей, приходим к следующему выражению:
![]()
Итак, сегментное (или каноническое) уравнение плоскости:
![]()
Упражнение 6
Вычисляет неявное или общее уравнение плоскости в пространстве, проходящей через точку.
![]()
и один из его нормальных векторов есть
![]()
Формула неявного, общего или декартова уравнения плоскости:
![]()
Ну а из вектора нормали мы можем найти коэффициенты A, B и C, потому что они соответственно равны компонентам вектора нормали:
![]()
Значит нам нужно найти только параметр D. Для этого подставим в уравнение координаты точки, принадлежащей плоскости:
![]()
![]()
![]()
![]()
![]()
В заключение, неявное или общее уравнение плана таково:
![]()
Упражнение 7
Найдите параметрические уравнения плоскости, содержащей прямую
![]()
и параллельно вправо
![]()
это строки:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-624f315685b292c4bb05e9cb4b931a97_l3.png)
Чтобы найти параметрические уравнения плоскости, нам нужно знать два вектора направления и точку на плоскости. Объявление сообщает нам, что оно содержит строку
![]()
Следовательно, мы можем взять вектор направления и точку на этой линии, чтобы определить плоскость. Более того, это утверждение говорит нам, что плоскость параллельна прямой.
![]()
поэтому мы также можем использовать вектор направления этой линии для уравнения плоскости.
право
![]()
выражается в виде параметрических уравнений, поэтому компонентами его вектора направления являются коэффициенты при параметрических членах
![]()
![]()
А декартовы координаты точки на этой же прямой являются независимыми членами параметрических уравнений:
![]()
С другой стороны, прямая линия
![]()
представляет собой непрерывное уравнение, такое, что компоненты его вектора направления являются знаменателями дробей:
![]()
Следовательно, параметрические уравнения плана имеют вид:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f5adabb85c9285653d6b638f7c48ba50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c81f4d8e5aa907f111b3389d5137736e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fccd86ac9a3e4084e324d8e5b1071e59_l3.png)