Параллельные плоскости

На этой странице вы найдете все о параллельных плоскостях: когда две плоскости параллельны, уравнения двух параллельных плоскостей, примеры, решенные упражнения, свойства,…

Что такое две параллельные плоскости?

В аналитической геометрии две плоскости параллельны, если они всегда находятся на одинаковом расстоянии друг от друга. Следовательно, две параллельные плоскости никогда не пересекаются и не имеют ничего общего.

Две плоскости, расположенные параллельно, не являются единственным возможным относительным положением между плоскостями, поскольку две плоскости в пространстве (в R3) также могут пересекаться или совпадать.

Как узнать, параллельны ли две плоскости?

Увидев определение параллельных плоскостей, давайте посмотрим, как можно определить, параллельны ли две плоскости или нет.

Начиная с общего (или неявного) уравнения двух разных планов:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

Две плоскости будут параллельны, если их коэффициенты A, B и C пропорциональны друг другу, а не коэффициенту D. Другими словами, параллельность между двумя плоскостями возникает, когда выполняется следующее уравнение:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

Пример двух параллельных плоскостей

Например, следующие две плоскости параллельны:

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

Планы параллельны, поскольку коэффициенты при переменных X, Y, Z пропорциональны друг другу, а не независимым членам:

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

Вычислить расстояние между двумя параллельными плоскостями

Две параллельные плоскости всегда находятся на одинаковом расстоянии, поэтому, чтобы найти расстояние между двумя параллельными плоскостями, мы можем взять точку на одной из двух плоскостей и вычислить расстояние от этой точки до другой плоскости. Следовательно, чтобы рассчитать расстояние между 2 параллельными плоскостями, необходимо знать формулу расстояния от точки до плоскости .

Это метод определения расстояния между двумя параллельными плоскостями. Однако есть еще более простой способ сделать это, когда коэффициенты А, В и С уравнений двух плоскостей совпадают:

Рассмотрим общие (или неявные) уравнения двух параллельных плоскостей:

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

Формула расчета расстояния между двумя параллельными плоскостями :

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

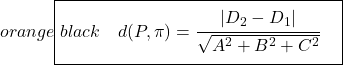
Так что, конечно, легче найти расстояние между двумя параллельными плоскостями, используя формулу, поскольку это всего лишь вопрос применения формулы и все, но это зависит от задачи. Кроме того, мы считаем, что лучше объяснить оба способа расчета расстояния, чтобы вы могли выбрать тот, который вам больше нравится.

Пример расчета расстояния между двумя параллельными плоскостями

В качестве примера мы рассчитаем расстояние между следующими двумя плоскостями:

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

Сначала мы должны убедиться, что мы имеем дело с двумя параллельными плоскостями. Таким образом, все коэффициенты уравнений плоскости пропорциональны, за исключением независимых членов, поэтому фактически они представляют собой две параллельные плоскости.

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

В этом случае члены А, В и С уравнений двух плоскостей не совпадают, но добиться этого можно, разделив все уравнение второй плоскости на два:

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

Итак, уравнения двух плоскостей теперь имеют одинаковые коэффициенты A, B и C. Поэтому мы можем легко вычислить расстояние между двумя плоскостями по формуле расстояния между двумя параллельными плоскостями:

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

Подставляем значения и решаем операции:

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

Так что расстояние между одной плоскостью и другой плоскостью равно единице.

Свойства параллельных плоскостей

Характеристики параллельных плоскостей следующие:

Рефлексивное свойство : каждая плоскость параллельна сама себе.

$\pi_1 \parallel \pi_1$

Свойство симметрии : если одна плоскость параллельна другой, то и эта плоскость параллельна первой. Этим свойством обладают и перпендикулярные плоскости.

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

Транзитивное свойство : если плоскость параллельна другой плоскости, а эта вторая плоскость параллельна третьей плоскости, то первая плоскость также параллельна третьей плоскости.

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$