Парабола (математика): определение, уравнение, элементы, примеры,…

На этой странице вы найдете все о параболе: что это такое, что она представляет, ее элементы (фокус, директриса, вершина и т. д.), ее уравнение (с различными типами уравнений параболы), примеры, решенные упражнения, его свойства, его применение…

Что такое притча?

Парабола – понятие, имеющее очень разные значения, но его математическое определение следующее:

В математике парабола — это геометрическое место точек на плоскости, которые равноудалены от фиксированной точки (называемой фокусом) и фиксированной линии (называемой директрисой).

Следовательно, любая точка параболы находится на одинаковом расстоянии от ее фокуса и директрисы.

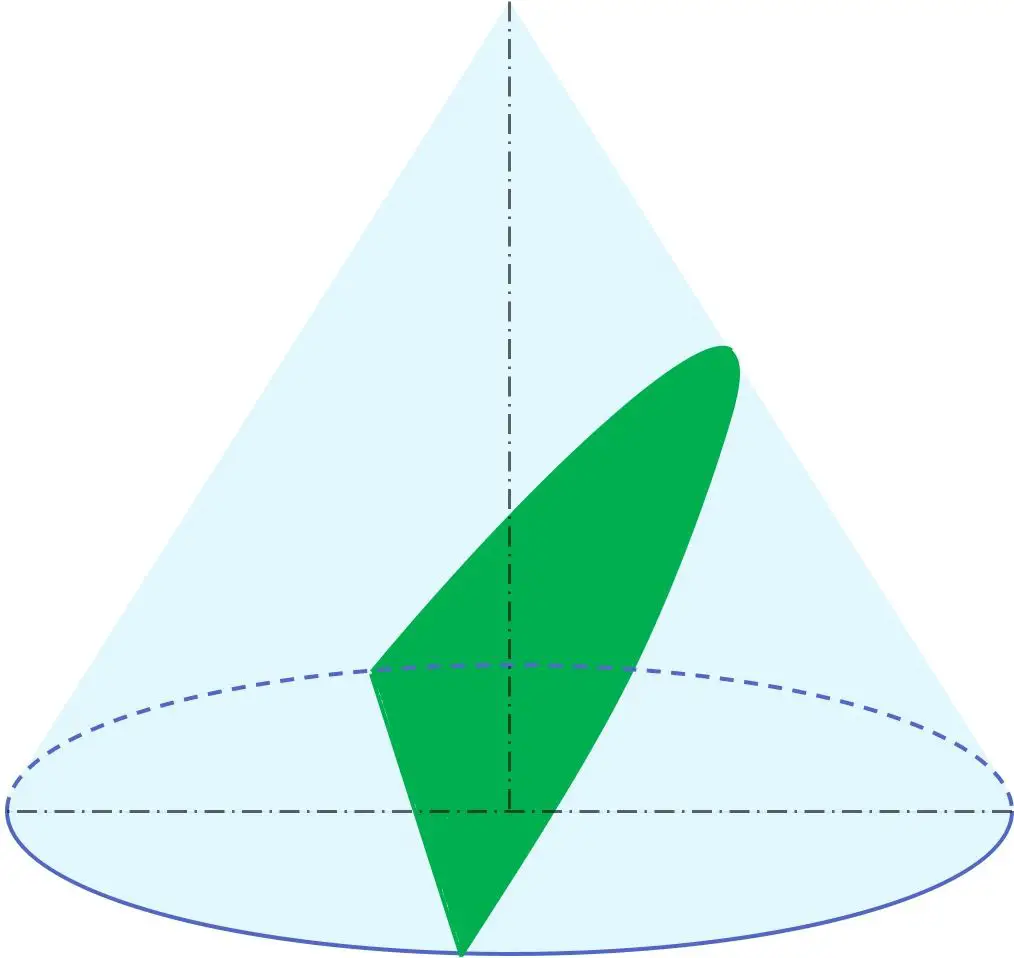
Кроме того, в геометрии парабола является одним из конических сечений наряду с окружностью, эллипсом и гиперболой. Другими словами, из конуса можно получить параболу.

В частности, парабола получается в результате сечения конуса плоскостью с углом наклона относительно оси вращения, эквивалентным углу образующей конуса. Следовательно, плоскость, содержащая параболу, параллельна образующей конуса.

Элементы параболы

Характеристики параболы зависят от следующих элементов:

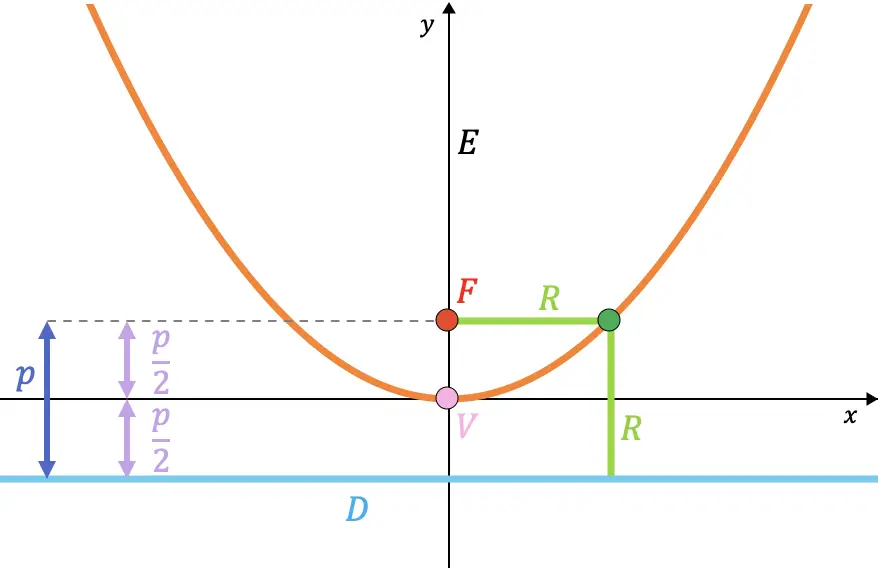
Фокус (F) : фиксированная точка внутри параболы. Расстояние от любой точки параболы до фокуса равно расстоянию от этой же точки до директрисы параболы.
Директриса (D) : это фиксированная линия, внешняя по отношению к параболе. Точка параболы находится на том же расстоянии от директрисы, что и от фокуса параболы.
Параметр (p) : расстояние от фокуса до режиссера.
Радиус-вектор (R) : отрезок, соединяющий точку параболы с фокусом. Его значение совпадает с расстоянием от точки до директрисы.
Ось (E) : линия, перпендикулярная директрисе, которая проходит через фокус и является осью симметрии параболы, на графике ниже она соответствует оси компьютера (ось Y). Также называется фокальной осью.
Вершина (V) : точка пересечения параболы и ее оси.
Фокусное расстояние : расстояние между фокусом и вершиной или между директрисой и вершиной. Его значение всегда равно
$\displaystyle \frac{p}{2}.$

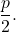
правая сторона

Правая часть параболы — это хорда внутри параболы, проходящая через фокус и параллельная директрисе.

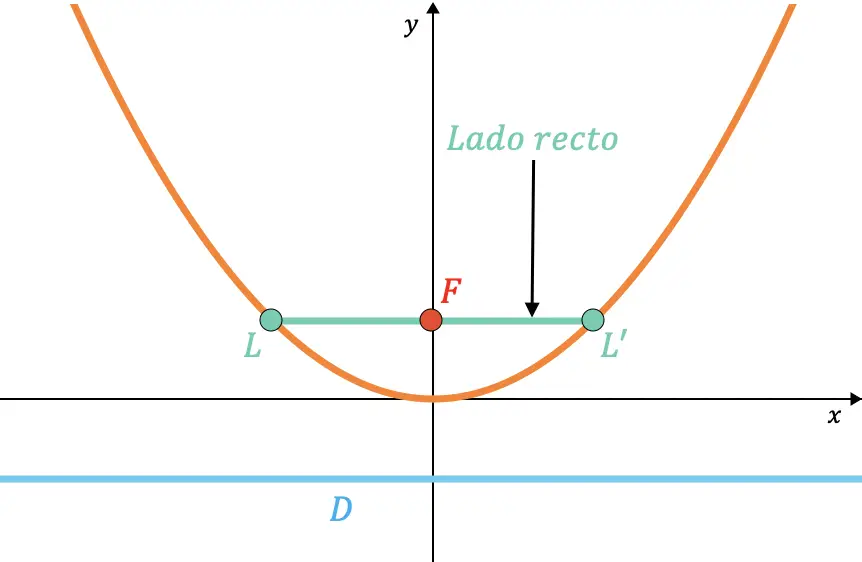
Аналогично можно показать, что длина правой части всегда в два раза больше значения параметра

$p.$

$\lvert LL'\rvert = 2p$

С другой стороны, две касательные к параболе линии, проходящие через концы правой стороны, образуют угол 45° с самой правой стороной и также пересекаются в вершине параболы.

уравнения параболы

Уравнение параболы является разновидностью квадратичной функции, поскольку оно всегда должно иметь хотя бы один член в квадрате. Кроме того, уравнение параболы зависит от ее горизонтальной или вертикальной ориентации.

Таким образом, в аналитической геометрии существует несколько способов математического выражения параболы: каноническое или приведенное уравнение , обыкновенное уравнение и общее уравнение параболы.

Приведенное или каноническое уравнение параболы

Что отличает приведенное или каноническое уравнение от других параболических уравнений, так это то, что вершина параболы является началом координат , то есть точкой (0,0).

Форма приведенного уравнения параболы зависит от того, горизонтальна она или вертикальна. Посмотрите на следующее графическое изображение, где указаны 4 возможных варианта:

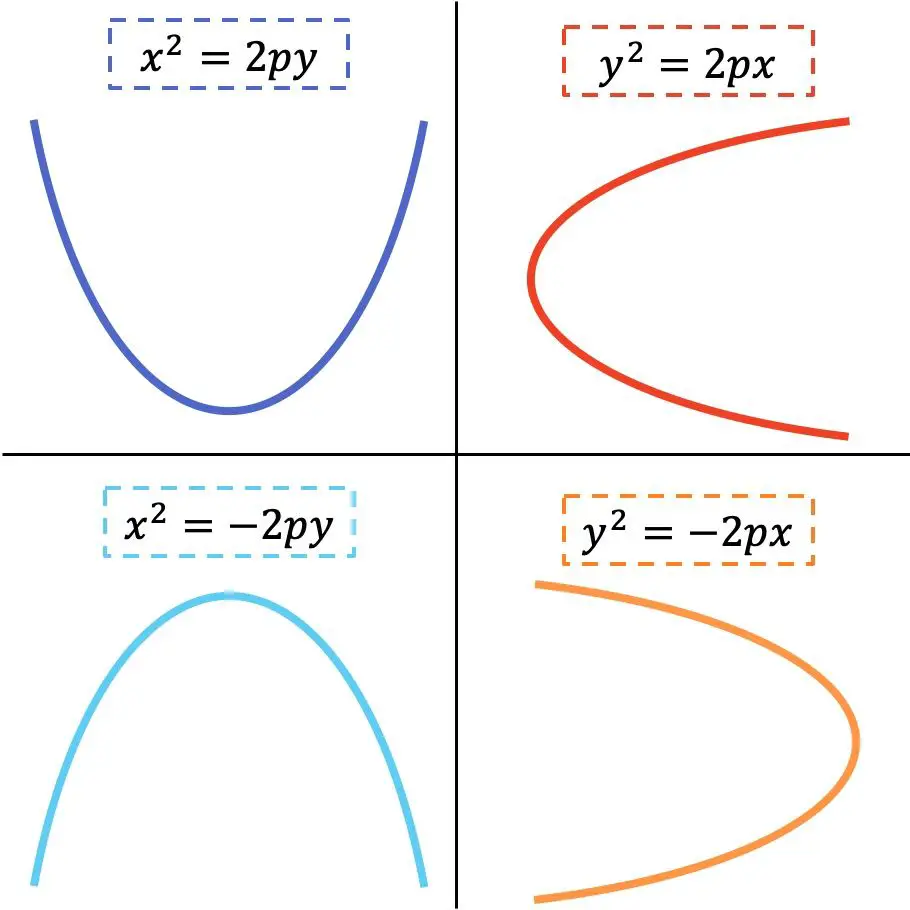
Золото

$p$

– характерный параметр параболы.

Как вы можете видеть на предыдущем изображении, когда переменная x возведена в квадрат, парабола вертикальна, а когда переменная y возведена в квадрат, парабола горизонтальна. С другой стороны, направление ветвей параболы зависит от знака уравнения.

Обычное уравнение параболы

Мы только что видели, как выглядит уравнение параболы, когда ее вершина или центр соответствует началу координат (приведенное или каноническое уравнение), но каково уравнение параболы, если вершина находится вне начала координат?

Когда вершиной параболы является любая точка, мы используем обычное уравнение параболы , выражение которого имеет вид:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}}(x-x_0 )^2 = 2p (y-y_0) \quad}$

где центром или вершиной параболы является точка

$V(x_0,y_0).$

Предыдущее уравнение соответствует параболе, ориентированной вертикально, то есть фокальная ось параболы параллельна оси Y.

Аналогично, чтобы определить параболу, ориентированную горизонтально (ее фокальная ось параллельна оси X), необходимо использовать следующий вариант обычного уравнения параболы:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} (y-y_0 )^2 = 2p (x-x_0)\quad}$

Где, как и прежде, центром или вершиной параболы является точка

$V(x_0,y_0).$

Общее уравнение параболы

До сих пор все уравнения параболы, которые мы проанализировали, используются для выражения горизонтальных или вертикальных парабол. Но очевидно , что парабола также может быть косой или наклонной .

Что ж, чтобы выразить этот тип параболы, мы используем общее уравнение параболы , формула которого выглядит следующим образом:

$\color{orange} \boxed{\color{black} \quad \vphantom{\frac{1}{2}} Ax^2 + Bxy+Cy^2 +Dx+Ey + F = 0 \quad}$

Приведенное выше уравнение является параболой тогда и только тогда, когда коэффициенты

$A$

$C$

одновременно не равны нулю и, кроме того, выполняется следующее условие:

$B^2-4AC =0$

Пример того, как найти вершину, фокус и директрису параболы по ее уравнению.

Во многих упражнениях и задачах с параболой вас просят вычислить вершину, фокус и директрису определенной параболы. Поэтому давайте посмотрим, как это делается на примере:

Найдите вершину, фокус и директрису следующей параболы:

$x^2 = 4y$

Фундаментальным моментом для решения задачи о параболе этого типа является определение параметра параболы p . В этом случае уравнению параболы соответствует приведенное или каноническое уравнение (вертикальная парабола):

$x^2 = 2py$

Следовательно, параметр p равен:

$2p = 4$

$p = \cfrac{4}{2}$

$p = 2$

С другой стороны, поскольку парабола следует приведенному или каноническому уравнению, это означает, что ее вершина или центр находится в начале координат:

$\bm{V(0,0)}$

Зная вершину и значение параметра параболы, мы легко можем найти ее фокус и директрису.

Квадратичным членом уравнения является переменная x , так что ось параболы будет параллельна оси OY и, фактически, поскольку ее вершиной является точка (0,0), ось параболы будет OY. сама ось. Тогда фокус параболы всегда находится на оси параболы и на расстоянии

$p/2$

от вершины параболы, поэтому ее координаты:

$\displaystyle F\left(0, \frac{p}{2} \right)$

$\displaystyle F\left(0, \frac{2}{2} \right)$

$\displaystyle \bm{F\left(0,1 \right)}$

Точно так же ориентиром будет горизонтальная линия, находящаяся на расстоянии

$p/2$

от вершины параболы, которая является началом координат. Таким образом, уравнение линии будет иметь вид:

$y=-\cfrac{p}{2}$

$y=-\cfrac{2}{2}$

$\bm{y=-1}}$

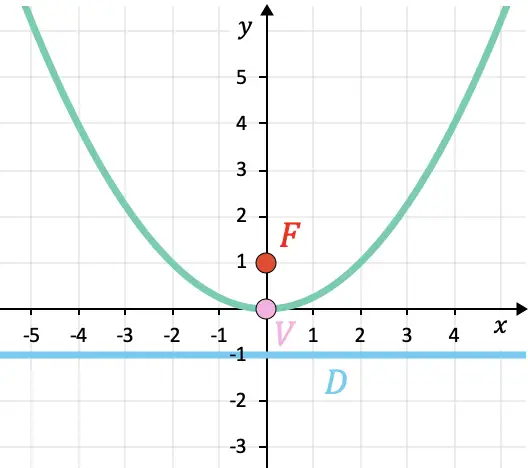
Ниже представлен график параболы, чтобы вы могли проверить результаты:

Упражнения по решению уравнения параболы

Свойства парабол

Все параболы обладают следующими свойствами:

Парабола — это разомкнутая кривая, или, другими словами, она состоит из двух ветвей, не имеющих общих точек и простирающихся неограниченным образом.
Каждая парабола имеет уникальную ось симметрии, где находится вершина указанной параболы.
Вертикально ориентированная парабола является выпуклой, когда ее ветви идут вверх; наоборот, парабола вогнута, если ее ветви идут вниз.
Эксцентриситет параболы эквивалентен единице (1). Эксцентриситет — это коэффициент, который в данном случае рассчитывается путем деления расстояния от фокуса до центра параболы на расстояние от вершины до директрисы (причем оба расстояния всегда совпадают по своему значению).
Из предыдущего свойства следует, что все параболы подобны или подобны.
Парабола не имеет асимптот.

параболические приложения

Теперь, когда вы хорошо знакомы со значением притчи, у вас может возникнуть вопрос… в чем смысл притчи?

Что ж, даже если вам это не кажется, геометрическая форма параболы очень распространена в реальной жизни. Например, во многих случаях при броске мяч совершает параболическое движение, особенно в баскетболе. Что ж, уравнение параболы очень полезно для аналитического изучения параболической траектории, по которой следует мяч.

Другое применение тарелки касается антенн (отсюда и название параболическая антенна). Поскольку каждый луч, попадающий на объект параболической формы, параллельный оси симметрии, отражается непосредственно в сторону фокуса, то есть все лучи, идущие к параболической антенне, концентрируются в фокусе и это можно использовать по-разному. Вот почему так важна направленность притчи.

Исправлены проблемы с блюдами

Упражнение 1

Вычислите вершину, фокус и директрису параболы, уравнение которой выглядит следующим образом:

$y^2 = 8x$

посмотреть решение

Во-первых, парабола будет горизонтальной, поскольку она следует следующему выражению приведенного или канонического уравнения параболы:

$y^2 = 2px$

Итак, его параметр p :

$2p = 8$

$p = \cfrac{8}{2}$

$p = 4$

$\bm{V(0,0)}$

Зная вершину и значение параметра параболы, мы можем легко вычислить ее фокус и директрису.

Квадратичный член уравнения является переменной, то есть ось параболы будет параллельна оси ОХ и, фактически, поскольку ее вершиной является точка (0,0), l ось параболы будет равна сама ось OX. Тогда фокус параболы всегда находится на оси параболы и на расстоянии

$p/2$

от вершины параболы, координаты которой:

$\displaystyle F\left(\frac{p}{2},0\right)$

$\displaystyle F\left(\frac{4}{2},0\right)$

$\displaystyle \bm{F\left(2,0 \right)}$

Аналогично, ориентир находится на расстоянии.

$p/2$

от вершины параболы, которая является началом координат и перпендикулярна ее фокальной оси. Следовательно, уравнение направляющей линии имеет вид:

$x=-\cfrac{p}{2}$

$x=-\cfrac{4}{2}$

$\bm{x=-2}}$

Упражнение 2

Найдите вершину, фокус и директрису параболы, уравнение которой имеет следующий вид:

$(x-4)^2 = -16(y+1)$

посмотреть решение

Парабола определяется в соответствии с ее обычным уравнением (ось, параллельная оси Y), формула которого имеет вид:

$(x-x_0 )^2 = 2p (y-y_0)$

Итак, его параметр p :

$2p = -16$

$p =- \cfrac{16}{2}$

$p =- 8$

С другой стороны, в этом случае из обычного уравнения параболы следует, что ее центр не находится в начале координат, с другой стороны, декартовыми координатами вершины параболы являются числа в скобках с измененным знаком. :

$\bm{V(4,-1)}$

Зная вершину и значение параметра параболы, мы можем вычислить ее фокус и директрису.

Квадратичным членом уравнения является переменная x , так что ось параболы параллельна оси OY. Таким образом, фокус параболы всегда находится на оси параболы и на расстоянии

$p/2$

от вершины параболы, так что координаты фокальной точки совпадают с координатами вершины, добавив

$p/2$

вертикально:

$\displaystyle F\left(4,-1+\frac{p}{2}\right)$

$\displaystyle F\left(4,-1+\frac{-8}{2}\right)$

$\displaystyle F\left(4,-1-4\right)$

$\displaystyle \bm{F\left(4,-5 \right)}$

Аналогично, директрисой будет горизонтальная линия, расположенная на расстоянии

$p/2$

от вершины параболы. Следовательно, уравнение направляющей линии имеет вид:

$y=-1-\cfrac{-p}{2}$

$y=-1-\cfrac{-8}{2}$

$y=-1+4$

$\bm{y=3}}$

Упражнение 3

Определите параболическое уравнение, ось которого параллельна оси абсцисс, имеет вершиной точку V(5,2), а фокусом является точка P(8,2).

посмотреть решение

В этом случае вершина параболы не является началом координат, поэтому нам нужно обычное уравнение, чтобы определить параболу утверждения. Также фокальная ось параболы параллельна оси X, а это значит, что парабола будет ориентирована горизонтально (ветви будут идти вправо или влево), и поэтому квадратичным членом уравнения должна быть переменная й :

$(y-y_0 )^2 = 2p (x-x_0)$