Относительное положение прямой и плоскости

На этой странице вы найдете относительные положения линии и плоскости. Мы объясним вам, как рассчитывается относительное положение между линией и плоскостью (2 метода), а также вы сможете увидеть примеры и упражнения, решаемые шаг за шагом.

Каковы относительные положения между прямой и плоскостью?

Прежде чем рассматривать все возможные относительные положения между линией и плоскостью, нам, очевидно, необходимо знать , что такое линии и что такое плоскость . Поэтому, если вам все еще не совсем ясны эти две концепции, мы рекомендуем вам сначала взглянуть на связанные страницы, где это подробно объяснено.

Таким образом, в аналитической геометрии существует только три относительных положения в пространстве между прямой и плоскостью:

Линия, содержащаяся в плоскости : когда линия содержится в плоскости, это означает, что они имеют бесконечное количество общих точек.
Параллельная линия и плоскость : Прямая и плоскость параллельны, если у них нет общей точки.
Пересекающаяся линия и плоскость : линия и плоскость пересекаются, когда линия пересекает плоскость в точке. Так что общего у них только одно.

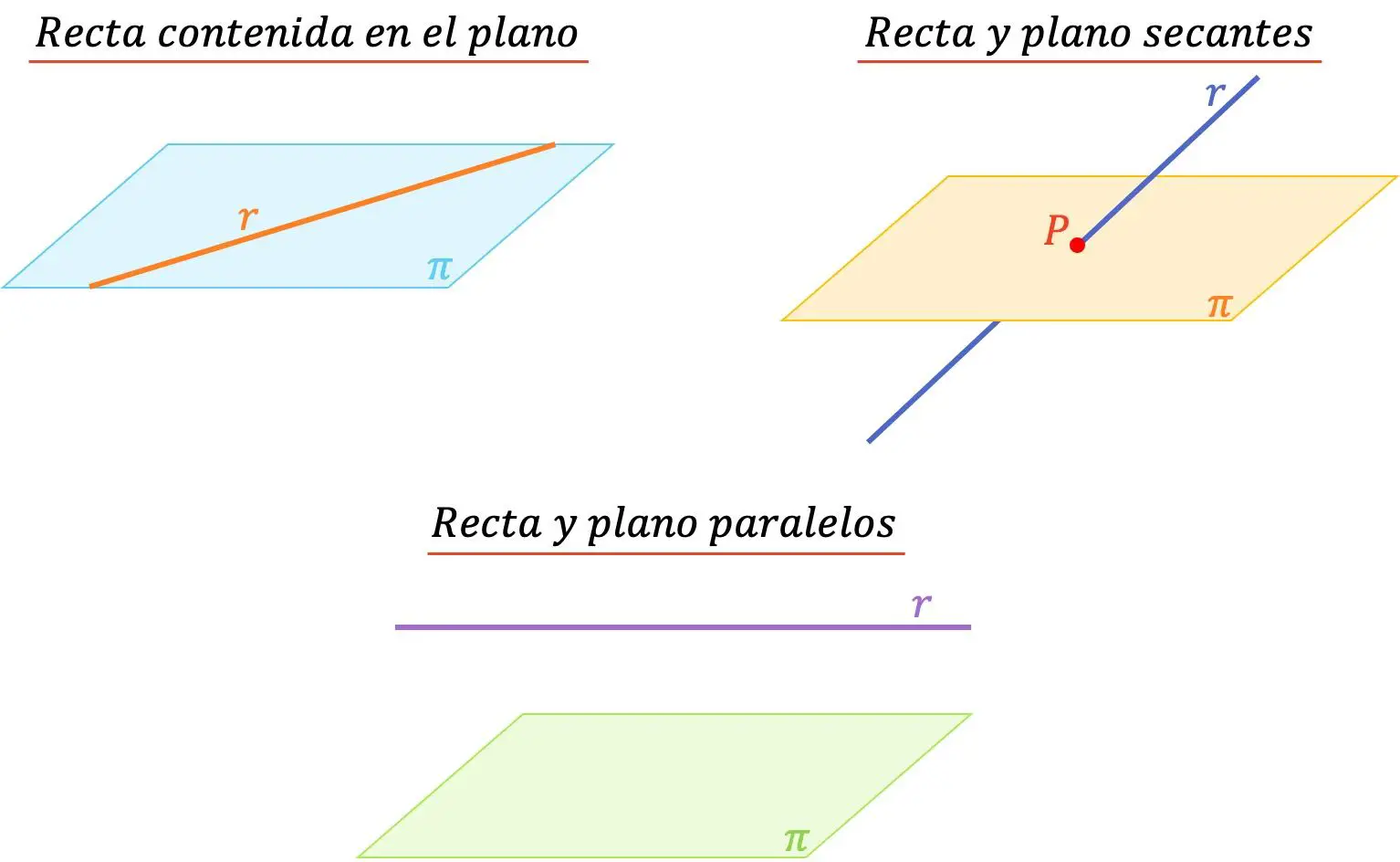
С другой стороны, когда линия содержится в плоскости или когда они параллельны друг другу, образуемый ими угол будет равен 0°. С другой стороны, при пересечении линии и плоскости угол между двумя геометрическими элементами может составлять от 0° (не входит в комплект) до 90° (включительно).

Как вычислить взаимное расположение линии и плоскости?

В основном существует два метода определения относительного положения между линией и плоскостью в пространстве: по диапазонам или по векторам .

Когда линия выражается в виде неявного (или общего) уравнения, проще использовать метод рангов. С другой стороны, если линия задана уравнением другого типа, например, когда она имеет форму векторного, параметрического или непрерывного уравнения, быстрее использовать векторный метод.

Если вы не помните, как выглядят уравнения линии, мы оставляем вам страницу, на которой вы можете ознакомиться со всеми уравнениями линии . Здесь вы найдете все уравнения прямой, формулы для быстрого нахождения уравнения прямой, проходящей через две точки, примеры и пошагово решаемые упражнения.

Поэтому практичнее использовать тот или иной метод в зависимости от проблемы, по этой причине мы рекомендуем вам знать, как выполнять обе процедуры. Ниже приводится объяснение обоих методов с примерами.

Когда линия имеет форму неявного (или общего) уравнения

Один из способов определить относительное положение линии и плоскости — вычислить ранг двух матриц.

Если линия определяется ее неявными (или общими) уравнениями:

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}$

И план также выражается в виде общего уравнения:

$\pi : \ A_3x+B_3y+C_3z+D_3=0$

Назовем А матрицей, составленной из коэффициентов А, В и С уравнений плоскости и прямой:

$\displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}$

А матрица A’ будет расширенной матрицей со всеми коэффициентами двух уравнений:

$\displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}$

Затем относительное положение между линией и плоскостью определяется значением протяженности двух предыдущих матриц согласно следующей таблице:

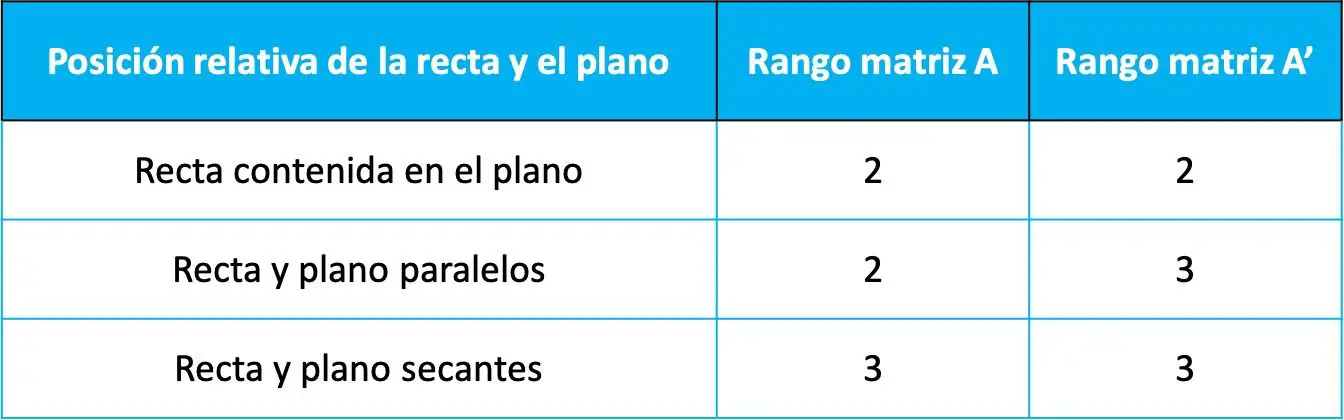
изучить относительное положение линии и плоскости в пространстве по диапазонам

То, что относительные положения зависят от рангов этих двух матриц, можно показать с помощью теоремы Руша-Фробениуса (теоремы, используемой для решения систем линейных уравнений). Однако на этой странице мы не будем проводить демонстрацию, потому что это не обязательно знать, и это тоже мало что дает.

Пример, как найти взаимное положение линии и плоскости по диапазонам

Чтобы вы могли видеть, как именно это делается, на примере решим упражнение:

Изучите относительное положение между следующей линией и следующей плоскостью:

$\displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}$

$\pi : \ 2x+2y-6=0$

Линия определяется двумя пересекающимися плоскостями, то есть выражается неявным уравнением. Поэтому мы будем использовать метод рангов для изучения относительного положения между линией и плоскостью.

Первое, что нужно сделать, это построить матрицу A и расширенную матрицу A’ с коэффициентами уравнений:

$\displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}$

И теперь нам нужно вычислить ранг каждой матрицы. Сначала находим размер матрицы А по определителям:

$rg(A) = \ ?$

$\displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0$

$\displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0$

$rg(A) = 2$

Определитель матрицы A равен нулю, но она содержит подматрицу размера 2 × 2, определитель которой отличен от нуля, поэтому это матрица ранга 2.

С другой стороны, необходимо также вычислить ранг матрицы A’. А диапазон расширенной матрицы A’ всегда будет как минимум таким же, как и у матрицы A, поэтому нам просто нужно проверить, имеет ли она ранг 3 или 2:

$rg(A') = \ ?$

$\displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0$

$rg(A') = 3$

С другой стороны, расширенная матрица A’ имеет субопределитель 3×3, отличный от 0, поэтому она имеет ранг 3.

Итак, поскольку матрица A имеет ранг 2, а матрица A’ имеет ранг 3, прямая и плоскость параллельны .

Когда линия имеет форму уравнения другого типа

Когда линия выражается уравнением, отличным от неявного, будь то векторное, параметрическое или непрерывное уравнение, предпочтительнее использовать метод, который мы объясним ниже.

Итак, если линия задана в виде векторного уравнения, параметрического уравнения или непрерывного уравнения, это означает, что мы знаем точку, принадлежащую прямой, а также ее вектор направления.

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}$

С другой стороны, мы также знаем, что такое нормальный (или перпендикулярный) вектор к плоскости:

$\vv{n} \perp \pi$

Затем, исходя из двух векторов и точки линии, относительное положение между линией и плоскостью можно вычислить следующим образом:

Если скалярное произведение вектора направления прямой и вектора нормали к плоскости отлично от нуля, это означает, что линия секущая к плоскости.

$\vv{\text{v}}_r\cdot \vv{n} \neq 0 \ \color{orange}\longrightarrow \color{black} \ \text{recta y plano secantes}$
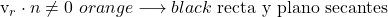
Но если скалярное произведение вектора направления прямой и вектора нормали к плоскости равно нулю, есть две возможности: линия содержится в плоскости или они параллельны. И чтобы узнать, в каком случае это так, мы должны подставить координаты точки на прямой в уравнение плоскости.
- Если точка удовлетворяет уравнению плоскости, линия содержится в плоскости.
- С другой стороны, если точка не удовлетворяет уравнению плоскости, линия и плоскость параллельны.

Пример определения взаимного положения линии и плоскости с помощью векторов

После того, как мы ознакомились с теорией этого метода, давайте теперь посмотрим, как поэтапно решить упражнение:

Найдите относительное положение между следующей линией и следующей плоскостью:

$\displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}$

$\pi : \ 2x+y-2z-3=0$

Во-первых, линия определяется как параметрические уравнения, поэтому ее вектор направления и точка, через которую она проходит, равны:

$\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}$

И, с другой стороны, вектор нормали к плоскости:

$\vv{n} =(2,1,-2)$

Как только мы узнаем вектор направления линии и вектор нормали к плоскости, мы должны вычислить скалярное произведение между ними:

$\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}$

Результат скалярного произведения равен нулю, поэтому линия может находиться только в плоскости или быть параллельной ей. Итак, чтобы выяснить, какой это случай, подставим декартовы координаты точки на прямой в уравнение плоскости:

$2x+y-2z-3=0 \ \xrightarrow{P(2,-1,0)} \ 2\cdot 2 -1 -2 \cdot 0 -3 = 0$

$4- 1 -0 -3 = 0$

$0 = 0$

Подставляя точку прямой в уравнение плоскости, получаем равенство, следовательно, точка подчиняется уравнению плоскости и, следовательно, прямая содержится в плоскости .