Взаимное положение двух линий в пространстве

Здесь вы найдете все относительные положения двух линий в пространстве (в R3). Кроме того, объясняется, как найти относительное положение между двумя линиями двумя возможными методами: по диапазонам или по точке и вектору каждой линии. Вы даже сможете увидеть примеры и упражнения, решаемые шаг за шагом.

Каково взаимное расположение двух линий в пространстве?

В аналитической геометрии при работе в трехмерном пространстве (в R3) существует 4 возможных относительных положения между двумя линиями: две линии могут быть сливающимися линиями , параллельными линиями , секущими линиями или секущими линиями .

Параллельные линии

относительное положение двух параллельных прямых

Две прямые параллельны, если они имеют одинаковое направление, но не имеют общей точки. Кроме того, параллельные линии всегда находятся на одинаковом расстоянии друг от друга.

совпадающие линии

относительное положение двух совпадающих линий

Две прямые совпадают, если они имеют одинаковое направление и, более того, все их точки общие.

пересекающиеся линии

относительное положение двух пересекающихся линий

Две пересекающиеся прямые имеют разные направления, но соприкасаются в одной точке.

Линии пересечения

Две пересекающиеся прямые имеют разные направления и не пересекаются ни в одной точке. Следовательно, две пересекающиеся линии не лежат в одной плоскости. Например, в графическом представлении над линией

$s$

всегда впереди линии

$r$

, поэтому они никогда не будут касаться друг друга.

Есть 2 способа узнать, каково относительное положение между двумя линиями, поскольку они зависят от того, как выражаются уравнения двух линий:

Если линии представлены в форме векторных, параметрических или непрерывных уравнений, лучше всего вычислять относительное положение по точке и вектору каждой линии (объяснение этого метода приведено ниже).
С другой стороны, если линии определены в форме неявных (или общих) уравнений, относительное положение между двумя линиями легче узнать, вычислив ранг двух матриц (см. объяснение ниже).

Определение взаимного положения двух линий по точке и вектору

Вы можете найти относительное положение между двумя линиями с помощью точки и вектора каждой линии. Этот метод целесообразно использовать, когда линии заданы в виде векторного уравнения, параметрического уравнения или непрерывного уравнения.

Таким образом, пусть вектор направления и любая точка на каждой из двух прямых будут:

$\displaystyle r: \ \begin{cases} \vv{\text{v}} = (\text{v}}_x, \text{v}}_y,\text{v}}_z})\\[2ex] P(P_x,P_y,P_z)\end{cases} \qquad\qquad s: \ \begin{cases} \vv{\text{v}}' = (\text{v}}_x', \text{v}}_y',\text{v}}_z'})\\[2ex] P'(P_x',P_y',P_z')\end{cases}$

Итак, чтобы найти взаимное положение двух линий, нам необходимо выполнить следующую процедуру:

‣ Первое, что нам нужно сделать, это посмотреть, пропорциональны ли векторы двух линий, и, в зависимости от случая, мы делаем следующее:

Если два вектора пропорциональны, линии могут быть параллельны или совпадать. Поэтому мы должны проверить, удовлетворяет ли точка одной линии уравнению другой линии:
- Если точка одной линии удовлетворяет уравнению другой линии, это означает, что две линии совпадают.
- В противном случае это означает, что две линии параллельны.
Если два вектора не пропорциональны, линии могут пересекаться или пересекаться. В этом случае мы должны решить следующий определитель 3×3:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$
- Если предыдущий определитель равен нулю, две прямые пересекаются в точке (они пересекаются).
- Если предыдущий определитель отличен от нуля, две линии пересекаются.

На следующем рисунке показана вся процедура:

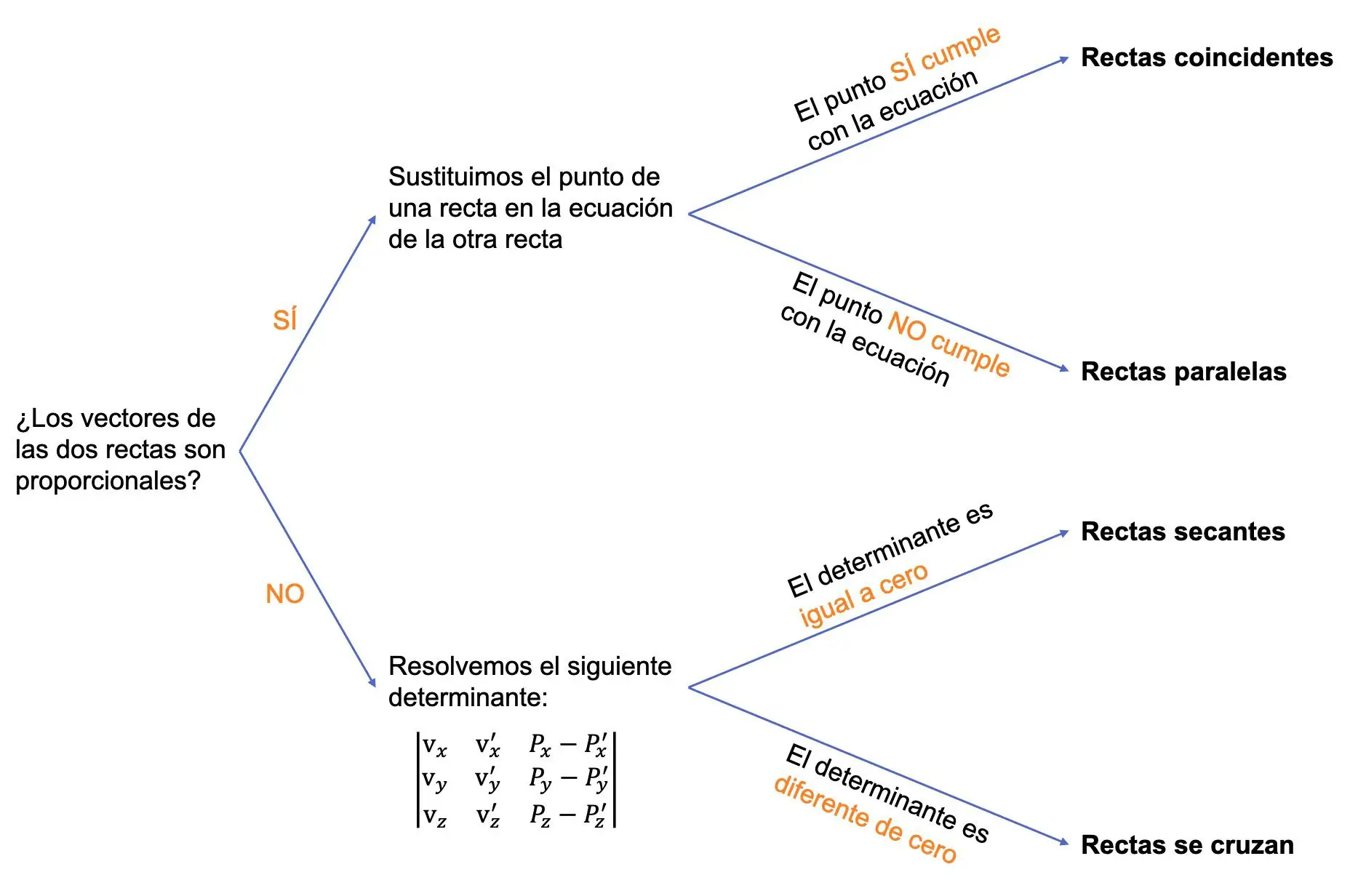
Пример определения относительного положения между двумя линиями

Предыдущая процедура может показаться немного сложной, но чтобы вы могли убедиться в обратном, в качестве примера решим задачу:

Определите относительное положение между следующими двумя строками:

$r: \ (x,y,z)=(2,0,1)+t(4,-1,1)$

$s: \ (x,y,z)=(1,-3,1)+t(1,2,0)$

Две линии выражаются в виде векторного уравнения, в котором вектор направления каждой линии равен:

$\vv{r} =(4,-1,1) \qquad \qquad \vv{s}=(1,2,0)$

И точка, через которую проходит каждая линия:

$R(2,0,1)\qquad \qquad S(1,-3,1)$

Как только мы узнаем точку и вектор направления каждой линии, мы применим метод, показанный выше. Прежде всего, мы должны проверить, пропорциональны ли координаты векторов:

$\cfrac{4}{1} \neq \cfrac{-1}{2} \neq \cfrac{1}{0} \quad \longrightarrow \quad \text{No proporcionales}$

Поскольку два вектора не пропорциональны друг другу, линии могут только касаться или пересекать друг друга. Следовательно, теперь нам нужно найти следующий определитель, образованный вектором направления и точкой на каждой прямой:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Подставляем значения в формулу:

$\begin{vmatrix} 4 & 1 & 2-1 \\[1.1ex] -1 & 2 & 0-(-3) \\[1.1ex]1& 0 & 1-1 \end{vmatrix}$

И вычисляем определитель, для этого можно использовать любой метод (правило Саррюса, метод дополнений или кофакторов и т.д.):

$\begin{vmatrix} 4 & 1 & 1 \\[1.1ex] -1 & 2 & 3 \\[1.1ex]1& 0 & 0 \end{vmatrix} = 1$

Если бы результат определения был нулевым, это означало бы, что линии пересекаются (соприкасаются). Но определитель отличен от 0, поэтому прямые пересекаются .

Найти относительное положение двух строк по строкам

Другой способ найти относительное положение двух строк — вычислить ранги двух конкретных матриц, как мы увидим дальше. Этот метод очень полезен, когда две линии представлены в неявной (или общей) форме уравнения.

Итак, если у нас есть две линии, выраженные их неявными (или общими) уравнениями в трехмерном пространстве (в R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Пусть A — матрица, составленная из коэффициентов двух строк:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

И учитывая расширенную матрицу A’, которая представляет собой матрицу, образованную всеми параметрами двух строк:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Затем относительное положение двух строк можно определить по диапазону двух предыдущих матриц согласно следующей таблице:

взаимное расположение двух строк по строкам

Следовательно, чтобы найти относительное положение между двумя строками, нам придется вычислить ранги двух матриц, и в зависимости от ранга каждой матрицы это будет тот или иной случай.

Эту теорему можно доказать с помощью теоремы Руше-Фробениуса (метода, используемого для решения систем линейных уравнений), однако на этой странице мы не будем проводить доказательство, поскольку оно довольно громоздкое и мало что добавляет.

Пример того, как найти взаимное положение двух строк по диапазонам

После того, как мы рассмотрели теорию относительного положения между двумя строками, давайте посмотрим, как она реализуется на примере:

Найдите относительное положение следующих двух строк:

$\displaystyle r: \ \begin{cases}3x+2y+z+4=0 \\[2ex] 4x+2z+2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}3x+4z-1=0 \\[2ex] x-5y-2z-2=0 \end{cases}$

Две линии представлены в форме общих (или неявных) уравнений, поэтому мы будем использовать метод рангов, чтобы найти относительное положение между двумя линиями. Поэтому мы строим матрицу A и расширенную матрицу A’ с коэффициентами строк:

$\displaystyle A=\begin{pmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{pmatrix}$

Когда у нас есть обе матрицы, нам нужно вычислить ранг каждой. Сначала вычислим ранг матрицы A по определителям:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}3 & 2 & 1\\[1.1ex]4 & 0 & 2\\[1.1ex]3 & 0 & 4 \end{vmatrix} = -20 \bm{\neq 0}$

$rg(A)=3$

Матрица A содержит определитель ненулевой подматрицы 3×3, поэтому матрица A имеет ранг 3 .

А теперь вычислим объем расширенной матрицы A’. Матрица A’ всегда будет иметь ранг не ниже матрицы A, которая в данном случае равна 3, поэтому достаточно проверить, имеет ли она ранг 4 или ранг 3. Для этого решаем определитель матрицы 4 × 4 с помощью дополнений (или кофакторов):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}3 & 2 & 1&4\\[1.1ex]4 & 0 & 2&2\\[1.1ex]3 & 0 & 4&-1\\[1.1ex]1 & -5 & -2 &-2 \end{vmatrix} =$

$\displaystyle =3 \cdot\begin{vmatrix} 0 & 2&2\\[1.1ex] 0 & 4&-1\\[1.1ex] -5 & -2 &-2 \end{vmatrix}-2\cdot\begin{vmatrix}4 & 2&2\\[1.1ex]3 & 4&-1\\[1.1ex]1 & -2 &-2 \end{vmatrix}+1\cdot\begin{vmatrix}4 & 0 &2\\[1.1ex]3 & 0 & -1\\[1.1ex]1 & -5 & -2 \end{vmatrix}-4\cdot \begin{vmatrix}4 & 0 & 2\\[1.1ex]3 & 0 & 4\\[1.1ex]1 & -5 & -2 \end{vmatrix}$

$\displaystyle =3 \cdot 50-2\cdot(-50)+1\cdot(-50)-4\cdot 50$

$\displaystyle =150+100-50-200$

$\displaystyle \bm{=0}$

$rg(A')=3$

Определитель всей расширенной матрицы равен нулю, поэтому матрица A’ также имеет ранг 3 .

Итак, матрица A и матрица A’ имеют ранг 3, следовательно, две прямые пересекаются . То есть между ними есть только одна точка пересечения.

$\color{orange} \boxed{\color{black} \quad rg(A) = rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Secantes} \quad \vphantom{\Bigl(}}$

Помните, что выше у вас есть таблица, в которой суммированы все возможные случаи относительных положений между двумя строками в соответствии с диапазонами матриц A и A’.

Решены проблемы относительного положения двух линий в пространстве.

Упражнение 1

Найдите относительное положение между следующими двумя строками:

$r: \ (x,y,z)=(3,4,0)+t(2,1,-3)$

$s: \ (x,y,z)=(1,-2,2)+t(0,5,1)$

посмотреть решение

Поскольку обе линии выражаются в виде векторного уравнения, мы найдем относительное положение между двумя линиями, используя метод одной точки и один вектор для каждой линии.

Вектор направления каждой линии:

$\vv{r} =(2,1,-3) \qquad \qquad \vv{s}=(0,5,1)$

И точка, принадлежащая каждой строке:

$R(3,4,0)\qquad \qquad S(1,-2,2)$

Таким образом, для применения процедуры необходимо сначала проверить, пропорциональны ли компоненты векторов направления:

$\cfrac{2}{0} \neq \cfrac{1}{5} \neq \cfrac{-3}{1} \quad \longrightarrow \quad \text{No proporcionales}$

Поскольку два вектора не пропорциональны друг другу, линии могут быть только пересекающимися или пересекающимися. Следовательно, теперь нам нужно найти следующий определитель, состоящий из вектора направления и точки на каждой прямой:

$\begin{vmatrix} \text{v}}_x & \text{v}}_x' & P_x-P_x' \\[1.1ex] \text{v}}_y & \text{v}}_y' & P_y-P_y' \\[1.1ex]\text{v}}_z & \text{v}}_z' & P_z-P_z' \end{vmatrix}$

Подставляем значения в формулу:

$\begin{vmatrix} 2 & 0 & 3-1 \\[1.1ex] 1 & 5 & 4-(-2) \\[1.1ex]-3& 1 & 0-2 \end{vmatrix}$

И вычисляем определитель:

$\begin{vmatrix} 2 & 0 & 2 \\[1.1ex] 1 & 5 & 6 \\[1.1ex]-3& 1 & -2 \end{vmatrix}= 0$

Результат определителя эквивалентен 0, поэтому линии пересекаются .

Упражнение 2

Вычислите относительное положение следующих двух линий:

$\displaystyle r: \ \begin{cases} x=3+2t \\[1.7ex] y=1+3t \\[1.7ex] z=2-t \end{cases} \qquad \qquad s: \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

посмотреть решение

Первая строка имеет форму параметрических уравнений, а вторая строка имеет форму непрерывного уравнения, с помощью которого мы определим относительное положение между двумя линиями методом одноточечного вектора каждой линии.

Координаты вектора направления вправо

$r$

коэффициенты перед параметром

$t,$

и координаты вектора направления прямой

$s$

— числа знаменателей:

$\vv{r} =(2,3,-1) \qquad \qquad \vv{s}=(-4,-6,2)$

И точка, принадлежащая каждой строке:

$R(3,1,2)\qquad \qquad S(-1,-5,4)$

$\cfrac{2}{-4} = \cfrac{3}{-6}= \cfrac{-1}{2} \quad \longrightarrow \quad \text{Proporcionales}$

Два вектора пропорциональны друг другу, поэтому линии могут быть только параллельными или совпадать. Чтобы снять это сомнение, необходимо заменить точку на прямой

$r$

в уравнении прямой

$s$

(или наоборот), чтобы увидеть, удовлетворяет ли он указанному уравнению:

$R(3,1,2) \ \longrightarrow \ \cfrac{x+1}{-4}=\cfrac{y+5}{-6} = \cfrac{z-4}{2}$

$\cfrac{3+1}{-4}=\cfrac{1+5}{-6} = \cfrac{2-4}{2}$

$\cfrac{4}{-4}=\cfrac{6}{-6} = \cfrac{-2}{2}$

$-1=-1 = -1$

Подставляя точку в прямую, мы получаем равенство, так что точка одной прямой удовлетворяет уравнению другой прямой и при этом их векторы направления пропорциональны. Следовательно, обе линии совпадают.

Упражнение 3

Найдите относительное положение следующих двух строк:

$\displaystyle r: \ \begin{cases}2x-2y-2z+5=0 \\[2ex] 2x-y-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}4x-y+2z+3=0 \\[2ex] x-2y-3z+6=0 \end{cases}$

посмотреть решение

Две линии представляют собой общую (или подразумеваемую) форму уравнения, поэтому мы будем использовать метод ранга, чтобы найти относительное положение между двумя линиями. Поэтому мы создаем матрицу A и расширенную матрицу A’ с коэффициентами строк:

$\displaystyle A=\begin{pmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3\end{pmatrix} \qquad \qquad A'=\begin{pmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{pmatrix}$

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]4 & -1 & 2 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -2 & -2\\[1.1ex]2 & -1 & 0\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 & -2\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix} =0 \qquad \begin{vmatrix}2 & -1 & 0\\[1.1ex]4 & -1 & 2\\[1.1ex]1 & -2 & -3 \end{vmatrix}=0$

$\displaystyle \begin{vmatrix}2 & -2 \\[1.1ex]2 & -1 \end{vmatrix}=2 \neq 0$

$rg(A)=2$

Все определители 3×3 матрицы A равны нулю, но внутри матрицы есть ненулевой определитель 2×2, поэтому матрица A имеет ранг 2 .

А теперь вычислим объем расширенной матрицы A’. Матрица A’ всегда будет как минимум диапазоном матрицы A, который в данном случае равен 2, поэтому необходимо проверить, имеет ли она определитель 3×3, который не сокращается, а также насколько велик определитель вся матрица:

$rg(A')= \ ?$

$\displaystyle \displaystyle \begin{vmatrix}2 & -2 & 5\\[1.1ex]2 & -1 &-1\\[1.1ex]4 & -1 &3\end{vmatrix}=22 \neq 0$

$\displaystyle det(A')=\begin{vmatrix}2 & -2 & -2&5\\[1.1ex]2 & -1 & 0&-1\\[1.1ex]4 & -1 & 2&3\\[1.1ex]1 & -2 & -3&6 \end{vmatrix}=0$

$rg(A')=3$

Расширенная матрица A’ действительно содержит 3×3 ненулевых подопределителя и, более того, определитель всей расширенной матрицы равен 0, поэтому матрица A’ имеет ранг 3 .

Итак, матрица A имеет ранг 2, а матрица A’ — ранг 3, поэтому две прямые параллельны . То есть у них нет ничего общего.

$\color{orange} \boxed{\color{black} \quad rg(A) = 2 \neq rg(A')= 3 \quad \longrightarrow \quad \text{Rectas Paralelas} \quad \vphantom{\Bigl(}}$

Помните, что в объяснении метода (выше) у вас есть таблица, в которой суммированы все возможные случаи взаимного расположения двух строк в соответствии с рангами матриц A и A’.

Упражнение 4

Найдите относительное положение следующих двух строк:

$\displaystyle r: \ \begin{cases}4x-y+2z=0 \\[2ex] x+y+3z-1=0 \end{cases}$

$\displaystyle s: \ \begin{cases}2x+5y-z-2=0 \\[2ex] 2x+3z+1=0 \end{cases}$

посмотреть решение

В этом случае две линии представлены в форме декартова (или неявного) уравнения, поэтому мы будем использовать метод упорядочивания, чтобы найти относительное положение между двумя линиями. Поэтому мы строим матрицу A и расширенную матрицу A’ с коэффициентами строк:

$\displaystyle A=\begin{pmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{pmatrix} \qquad \qquad A'=\begin{pmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{pmatrix}$

Зная две матрицы, нам нужно вычислить ранг каждой. Сначала вычислим ранг матрицы A по определителям:

$rg(A)= \ ?$

$\displaystyle \begin{vmatrix}4 & -1 & 2\\[1.1ex]1 & 1 & 3\\[1.1ex]2 & 5 & -1 \end{vmatrix} = -65 \bm{\neq 0}$

$rg(A)=3$

Матрица A содержит подматрицу размером 3×3, определитель которой ненулевой, поэтому матрица A имеет ранг 3 .

А теперь вычислим объем расширенной матрицы A’. Матрица A’ всегда будет иметь ранг не ниже матрицы A, которая в данном случае равна 3, поэтому достаточно проверить, имеет ли она ранг 4 или ранг 3. Для этого решаем определитель набор матрицы 4×4 сложениями (или кофакторами):

$rg(A')= \ ?$

$\displaystyle det(A')=\begin{vmatrix}4 & -1 & 2&0\\[1.1ex]1 & 1 & 3&-1\\[1.1ex]2 & 5 & -1&-2\\[1.1ex]2 & 0 & 3 &1 \end{vmatrix} =$

$\displaystyle =4 \cdot\begin{vmatrix} 1 & 3&-1\\[1.1ex] 5 & -1&-2\\[1.1ex] 0 & 3 &1 \end{vmatrix}-(-1)\cdot\begin{vmatrix}1 & 3&-1\\[1.1ex]2 & -1 & -2\\[1.1ex]2 & 3 &1 \end{vmatrix}+2\cdot\begin{vmatrix}1 & 1 &-1\\[1.1ex]2 & 5 & -2\\[1.1ex]2 & 0 &1 \end{vmatrix}-0\cdot \begin{vmatrix}1 & 1 & 3\\[1.1ex]2 & 5 & -1\\[1.1ex]2 & 0 & 3 \end{vmatrix}$

$\displaystyle =4 \cdot(-25)+1\cdot(-21)+2\cdot 9$

$\displaystyle =-100-21+18$

$\displaystyle =-103\bm{\neq0}$

$rg(A')=4$

Определитель всей расширенной матрицы ненулевой, поэтому матрица A’ имеет ранг 4 .

Итак, матрица A имеет ранг 3, а матрица A’, наоборот, имеет ранг 4, поэтому две прямые пересекаются в точке.

$\color{orange} \boxed{\color{black} \quad rg(A) = 3 \neq rg(A')= 4 \quad \longrightarrow \quad \text{Rectas se cruzan} \quad \vphantom{\Bigl(}}$

Помните, что в объяснении процедуры (выше) у вас есть таблица, в которой приведены все возможные случаи взаимного расположения двух строк в соответствии с рангами матриц A и A’.

Каково взаимное расположение двух линий в пространстве?

Определение взаимного положения двух линий по точке и вектору

Пример определения относительного положения между двумя линиями

Найти относительное положение двух строк по строкам

Пример того, как найти взаимное положение двух строк по диапазонам

Решены проблемы относительного положения двух линий в пространстве.

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ