Взаимное положение двух линий на плоскости

На этой странице вы найдете объяснение различных существующих методов определения взаимного положения двух линий на плоскости (в R2). Кроме того, вы увидите несколько примеров и сможете попрактиковаться, выполняя упражнения, решая шаг за шагом.

Каково взаимное расположение двух прямых на плоскости?

Прежде чем смотреть на относительное положение между двумя линиями на плоскости, очевидно, вам нужно точно знать, что такое линия, вы можете найти это в определении линии .

Таким образом, при работе в двух измерениях (в R2) возможны 3 типа относительных положений между двумя линиями:

пересекающиеся линии

относительное положение двух пересекающихся линий

Две пересекающиеся прямые имеют только одну общую точку.

Параллельные линии

относительное положение параллельных линий

Две прямые параллельны, если они не имеют общей точки. Это если их пути никогда не пересекутся.

совпадающие линии

относительное положение совпадающих линий

Две прямые называются одинаковыми, если все их точки общие.

С другой стороны, угол между двумя линиями на плоскости также зависит от их взаимного положения:

Пересекающиеся линии пересекаются под углом от 0° (не входит в комплект) до 90° (включительно). Кроме того, если они образуют прямой угол 90°, это означает, что две линии перпендикулярны.
Параллельные линии образуют угол 0°, так как имеют одинаковое направление.
И по той же причине совпадающие линии также составляют между собой угол 0°.

Если вы хотите узнать, как рассчитывается угол между двумя линиями, вы можете проверить формулу угла между двумя линиями . Здесь вы найдете подробное объяснение того, как определить угол между двумя линиями, а также несколько примеров и даже решенных упражнений, чтобы вы могли попрактиковаться и полностью понять эту концепцию.

Как найти взаимное положение двух прямых на плоскости

Знание относительного положения между двумя линиями в двумерном пространстве зависит от того, как они выражены:

Векторы направления линий: если две линии имеют разные вектора направления, они должны пересечься. С другой стороны, если координаты их векторов направления равны или пропорциональны, они могут быть параллельны или совпадать (необходимо проверить, есть ли у них общая точка).

Явное уравнение: когда две линии имеют разные наклоны
$(m)$

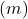
они высыхают. Напротив, если линии имеют одинаковый наклон, но разный порядок в начале координат.

$(n)$

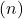
они параллельны. Наконец, две линии путаются, если изначально они имеют равные наклоны и ординаты.

Общее (или неявное) уравнение: две прямые с непропорциональными коэффициентами A и B всегда будут пересекаться. Однако они будут параллельны, когда эти два параметра пропорциональны друг другу, но не коэффициенту С. И, наконец, когда три члена пропорциональны, это означает, что линии перепутаны.

Если у вас есть какие-либо сомнения относительно приведенных выше уравнений прямой, вы можете обратиться к объяснению уравнений прямой на плоскости . Здесь вы найдете формулы всех уравнений линий, способы их расчета, примеры и решения уравнений линий.

В следующей таблице представлена сводка предыдущих свойств:

относительное положение двух линий на плоскости

Далее мы увидим два примера того, как определить относительное положение между двумя строками:

Пример 1

Найдите относительное положение между следующими двумя линиями, заданными в виде явного уравнения:

$r: \ y=3x+2 \qquad \qquad s: \ y=3x-4$

Обе линии имеют одинаковый наклон:

$m_r = m_s = 3$

Но у них в начале разные компьютеры:

$n_r =2\neq n_s=-4$

Итак, поскольку они имеют одинаковый наклон, но разные точки пересечения, линии параллельны .

Пример 2

Определите относительное положение между следующими двумя линиями, выраженными их неявным (или общим) уравнением:

$r: \ 4x+2y-6=0 \qquad \qquad s: \ -2x-y+3=0$

Обе линии выражаются в виде явного уравнения, поэтому нам нужно посмотреть, пропорционален ли какой-либо из их коэффициентов:

$\cfrac{4}{-2}=\cfrac{2}{-1} = \cfrac{-6}{3} = -2$

3 члена линий пропорциональны, поэтому линии совпадают .

Определить взаимное положение двух прямых на плоскости с помощью системы уравнений

Другой способ узнать взаимное положение между двумя линиями — проанализировать систему уравнений, образованную уравнениями линий:

Если система имеет единственное решение , то прямые пересекаются. Кроме того, точка пересечения двух прямых является решением системы.
Если это система без решения , это указывает на то, что прямые не имеют общих точек и, следовательно, являются параллельными прямыми.
Если система имеет бесконечно много решений , это означает, что прямые имеют все точки общие и, следовательно, являются пересекающимися прямыми.

Пример 3

Рассчитайте взаимное положение следующих двух линий, используя систему уравнений:

$r: \ 3x+4y+5=0 \qquad \qquad s: \ 5x+y-3=0$

Чтобы найти взаимное положение двух линий, нам нужно решить следующую систему линейных уравнений, образованную двумя линиями:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\}$

В этом случае будем решать систему методом замены. Поэтому мы изолируем переменную

$y$

из второго уравнения и подставим его в первое уравнение:

$\left.\begin{array}{l} 3x+4y+5=0\\[2ex] 5x+y-3=0\end{array}\right\} \begin{array}{l} \\[2ex] \longrightarrow \ y=3-5x \end{array}$

$3x+4(3-5x)+5=0$

$3x+12-20x+5=0$

$3x-20x=-12-5$

$-17x=-17$

$x=\cfrac{-17}{-17} = 1$

И как только мы узнаем, сколько стоит неизвестное

$x$

Подставим его значение в найденное выражение для

$y:$

$y=3-5x \ \xrightarrow{x \ = \ 1} \ y = 3 -5\cdot 1$

$y = 3 -5 = -2$

Таким образом, мы получили только одно решение системы уравнений, состоящей из двух линий, поэтому две линии пересекаются . А точка их пересечения есть решение системы, т. е. точка

$(1,-2).$

Решены задачи взаимного расположения двух линий на плоскости.

Упражнение 1

Определите, пересекаются ли, параллельны или совпадают следующие прямые:

$r: \ 3x-y+4=0 \qquad \qquad s: \ 9x-3y+3=0$

посмотреть решение

Обе линии выражаются в виде неявного (или общего) уравнения, поэтому нам нужно посмотреть, пропорционален ли какой-либо из их коэффициентов:

$\cfrac{3}{9}=\cfrac{-1}{-3} \neq \cfrac{4}{3}$

Только коэффициенты A и B прямых пропорциональны друг другу, а не коэффициенту C. Следовательно, две прямые параллельны .

Упражнение 2

Найдите относительное положение между следующими двумя линиями, выраженными в виде параметрических уравнений:

$\displaystyle r: \ \begin{cases} x=4-5t \\[2ex] y= 1+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=-2t \\[2ex] y=6+9t \end{cases}$

посмотреть решение

Мы могли бы решить систему уравнений, образованную двумя линиями, чтобы найти их взаимное расположение. Однако, поскольку они имеют форму параметрических уравнений, их векторы направления легко найти, и если они не пропорциональны, то это означает, что прямые пересекаются. И в этом случае мы не будем тратить столько времени на решение целой системы уравнений.

Так что декартовы координаты вектора направления каждой линии — это числа перед параметром

$t:$

$\vv{r} =(-5,3) \qquad \qquad \vv{s}=(-2,9)$

Зная векторы направления, мы проверяем их пропорциональность:

$\cfrac{-5}{-2} \neq \cfrac{3}{9}$

Векторы направления не пропорциональны, поэтому линии пересекают друг друга .

Упражнение 3

Укажите, пересекаются ли следующие прямые, параллельны или совпадают, а также найдите точку пересечения между ними (если применимо).

$r: \ y=4x-5 \qquad \qquad s: \ y=-2x+7$

посмотреть решение

Две линии определяются их явным уравнением и имеют разные наклоны:

$m_r =4 \neq m_s = -2$

Поскольку они имеют разный наклон, линии пересекаются .

Следовательно, поскольку линии пересекаются, они будут иметь 1 общую точку и для ее расчета нам необходимо решить систему уравнений, образованную двумя линиями:

$\left.\begin{array}{l} y=4x-5\\[2ex] y=-2x+7\end{array}\right\}$

В этом случае мы будем решать систему методом уравнения, поскольку оба

$y$

уже удалены:

$y=y$

$4x-5=-2x+7$

$4x+2x=5+7$

$6x=12$

$x=\cfrac{12}{6} = 2$

И как только у нас появится неизвестное

$x$

мы подставляем его значение в любое выражение

$y$

чтобы узнать, сколько это стоит:

$y=4x-5$

$y = 4\cdot 2 -5 = 8 -5 = 3$

Таким образом, точка пересечения двух линий является результатом работы системы:

$\bm{(2,3)}$

Упражнение 4

Вычислить значение неизвестных

$a$

$b$

так, чтобы следующие две прямые были параллельны:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

посмотреть решение

Линии описываются в общей (или неявной) форме уравнений. Следовательно, чтобы две прямые были параллельны, их коэффициенты A и B должны быть пропорциональны, то есть должно выполняться следующее уравнение:

$\cfrac{2}{1} = \cfrac{-4}{a}$

Поэтому мы должны решить предыдущее уравнение, чтобы получить значение неизвестного.

$a.$

Для этого умножим дроби крест-накрест:

$2 \cdot a = -4 \cdot 1$

$a = \cfrac{-4}{2}$

$\bm{a=-2}$

С другой стороны, чтобы прямые были параллельными, их независимые члены не могут быть пропорциональны остальным коэффициентам:

$\cfrac{2}{1} \neq \cfrac{6}{b}$

Поэтому, как и раньше, решаем неравенство умножением дробей крест-накрест:

$2 \cdot b \neq 6 \cdot 1$

$b \neq \cfrac{6}{2}$

$\bm{b\neq 3}$

Короче говоря, чтобы две линии были параллельны.

$a$

должно быть 2 и

$b$

может быть любым действительным числом, кроме 3.

Упражнение 5

Найдите явное уравнение прямой, параллельной прямой

$r$

и что происходит через точку

$P(3,-1).$

быть прямым

$r:$

$r: \; y=2x+5$

посмотреть решение

Чтобы линия была параллельна линии

$r,$

оба должны иметь одинаковый наклон. и наклон линии

$r$

это 2:

$m = 2$

Следовательно, уравнение прямой, которую нам нужно найти, будет иметь вид:

$y=2x+n$

И как только мы узнаем наклон линии, мы можем вычислить точку пересечения оси y, подставив точку, принадлежащую линии, в уравнение линии:

$P(3,-1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=-1} \ -1=2\cdot 3 +n$

$-1=6+ n$

$-1-6= n$

$-7= n$

Итак, явное уравнение линии:

$\bm{y=2x-7}$

Если вы зашли так далеко, значит, вы уже освоили относительные положения между двумя линиями на плане. Отличная работа!

Но многие задаются вопросом: а какой смысл знать относительное положение между двумя линиями?

Что ж, одно из применений относительного положения между строками — это возможность узнать расстояние между двумя строками, поскольку расчет расстояния между двумя строками зависит от их относительного положения:

Если линии пересекаются или совпадают, расстояние равно нулю.
С другой стороны, когда линии параллельны, необходимо применить определенную формулу. Если вас больше интересует, вы можете узнать, как рассчитывается расстояние между двумя параллельными линиями .

Каково взаимное расположение двух прямых на плоскости?

Как найти взаимное положение двух прямых на плоскости

Пример 1

Пример 2

Определить взаимное положение двух прямых на плоскости с помощью системы уравнений

Пример 3

Решены задачи взаимного расположения двух линий на плоскости.

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Упражнение 5

Оставьте комментарий Отменить ответ