В этой статье мы объясним, какие операции можно выполнять с функциями. Вы сможете увидеть пояснения, а также решенные упражнения по работе с функциями. И наконец, вы найдете свойства операций с функциями.
Что такое операции с функциями?
С функциями можно выполнять 5 различных типов операций: сложение, вычитание, произведение, деление и композиция. То есть две функции можно складывать, вычитать, умножать, делить или составлять.
Далее мы увидим, как осуществляется каждый тип операции с функциями и характеристиками каждой из них.
Сумма функций
Значение суммы (или сложения) двух функций равно сумме значений каждой функции. Другими словами, чтобы вычислить образ функции суммы, просто сложите изображения функций, участвующих в операции.
![]()
Более того, область определения суммы двух функций является пересечением области определения каждой суммируемой функции.
![]()
Давайте посмотрим, как добавляются две функции на примере:
![]()
Сначала мы добавляем две функции:
![]()
И теперь мы находим область определения функции суммы. Для этого вычислим область определения каждой функции отдельно:
![]()
➤ См.: как вычислить область определения функции.
Тогда область определения функции, полученной в результате операции, будет:
![]()
Каждая операция с функциями должна сопровождаться ее областью определения, чтобы полностью определить результат.
Вычитание функций
Образ вычитания (или разности) двух функций — это вычитание образов каждой функции, участвующей в операции:
![]()
Как и в случае с функцией сложения, область вычитания двух функций эквивалентна пересечению области определения каждой функции.
![]()
Итак, если функция не определена при определенном значении независимой переменной x, то и функция, полученная в результате вычитания, не будет определена.
Давайте посмотрим, как вычитаются две функции, на примере:
![]()
Сначала вычитаем две функции:
![]()
А затем определяем область определения функции вычитания:
![]()
![]()
Флагманский продукт
Чтобы вычислить произведение или (умножение) двух функций , вам просто нужно перемножить выражения каждой функции.
![]()
С другой стороны, область определения функции произведения представляет собой набор пересечений области определения каждой умноженной функции.
![]()
Например, если у нас есть следующие две функции:
![]()
Сначала выполняем работу изделия с двумя функциями:
![]()
И, наконец, находим область определения функции, полученной в результате операции:
![]()
![]()
Распределение функций
Численный результат деления (или частного) двух функций соответствует следующему уравнению:
![]()
Однако областью деления двух функций является множество пересечений области определения каждой функции за вычетом всех x, которые отменяют функцию, действующую как делитель, потому что в противном случае мы получили бы неопределенность.
![]()
В качестве примера мы разделим следующие функции:
![]()
Распределение функций следующее:
![]()
С другой стороны, область определения каждой функции в отдельности состоит из всех действительных чисел.
![]()
Однако, поскольку в знаменателе дроби не может быть нуля, в области определения результирующей функции необходимо удалить все значения, сокращающие знаменатель (х=3).
![]()
Состав функций
Композиция функций — самая сложная операция, поскольку это самая сложная концепция.
Композиция функций состоит из последовательного применения двух функций. Алгебраически композиция двух функций выражается следующим образом:
![]()
С другой стороны, область композиции функций
![]()
эквивалентно множеству всех значений x в области определения функции
![]()
такой как
![]()
принадлежит области функции
![]()
![]()
Например, учитывая следующие две функции:
![]()
Чтобы найти составную функцию
![]()
с последующим
![]()
нам нужно заменить выражение
![]()
где есть один
![]()
в выражении
![]()
![Rendered by QuickLaTeX.com \begin{aligned}(g\circ f)(x)&=g\Bigl(f(x)\Bigr)\\[2ex]&= g\Bigl(x^2+1\Bigr)\\[2ex]&=3(x^2+1)-4\\[2ex]&=3x^2+3-4\\[2ex]&=3x^2-1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f48079d61cf80409fdbf6610b5724189_l3.png)
В этом случае область определения обеих функций полностью состоит из действительных чисел, поэтому область определения составной функции также будет состоять из вещественных чисел.
![]()
Как видите, составление функций — непростая для понимания операция. Поэтому мы рекомендуем вам попрактиковаться в следующих упражнениях на композицию функций:
➤ См.: решенные упражнения на состав функций.
Свойства операций с функциями
Из всех операций с функциями сумма и произведение характеризуются следующими свойствами:
- Ассоциативное свойство : порядок сложения или умножения 3 или более функций не имеет значения.
![]()
![]()
- Коммутативное свойство : порядок сложения или умножения двух функций не меняет результат.
![]()
![]()
- Нейтральный элемент: операция суммы и операция произведения имеют постоянные функции нейтрального элемента.
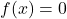
И
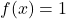
соответственно.
- Симметричный элемент : функция суммы имеет противоположную функцию.
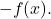
- Распределительное свойство : это свойство связывает сумму и произведение операций и основано на следующем равенстве:
![]()