На этой странице мы увидим, как обсуждать и решать систему уравнений с параметрами . Кроме того, вы найдете примеры и решенные упражнения систем линейных уравнений для практики.
С другой стороны, для анализа систем линейных уравнений важно знать , что такое правило Крамера и что такое теорема Руше-Фробениуса , потому что мы будем ими постоянно пользоваться.
Пример системы линейных уравнений с параметрами
- Обсудите и решите следующую систему уравнений относительно параметра m :
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+my+2z=0 \\[1.5ex] 3x+mz = 4\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6ab2286d15c20029b98a5ea4622033d4_l3.png)
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
Теперь мы решаем определитель A, используя правило Сарруса, чтобы увидеть, какого ранга матрица:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} & =m^2+6+0-6m-0+m \\ & = m^2-5m+6 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e823f83f25f798bd854612a7352680d4_l3.png)
Таким образом, результат определителя A зависит от значения m . Поэтому мы увидим, при каких значениях m определитель обращается в нуль. Для этого мы устанавливаем результат равным 0 :
![]()
И решаем квадратное уравнение по формуле:
![]()
![Rendered by QuickLaTeX.com \displaystyle m = \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1 \cdot 6}}{2 \cdot 1} = \cfrac{5 \pm \sqrt{25-24}}{2} =\cfrac{5 \pm 1}{2} = \begin{cases} \bm{m = 3} \\[2ex] \bm{m =2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e863082ac1f9b43df4de9fe93f5eb305_l3.png)
Итак, когда m равно 2 или 3, определитель A будет 0. А когда m отличается от 2 и отличается от 3, определитель A будет отличен от 0.
Поэтому мы должны анализировать каждый случай отдельно:
м≠3 и м≠2:
Как мы только что видели, когда параметр m отличается от 2 и 3, определитель матрицы A отличен от 0. Следовательно, ранг матрицы A равен 3 .
![]()
Более того, ранг матрицы A’ тоже равен 3 , поскольку внутри нее есть подматрица 3×3, определитель которой отличен от 0. И она не может иметь ранг 4, поскольку «мы не можем составить определитель 4×4.
![]()
Тогда, поскольку ранг матрицы A равен рангу матрицы A’ и числу неизвестных системы (3), по теореме Руше-Фробениуса мы знаем, что это совместимая детерминированная система (SCD). :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-557185e16670c72d23eec5a3ea13b487_l3.png)
Как только мы узнаем, что система является совместимой детерминированной системой (DCS), мы применим правило Крамера для ее решения. Для этого напомним, что матрица А, ее определитель и матрица А’ равны:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & m & 2 & 0 \\[1.1ex] 3 & 0 & m & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bef8e6b26595703c77c65178cbf90ffc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 2 \\[1.1ex] 3 & 0 & m \end{vmatrix} = m^2-5m+6](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac47361358555f733a42cffecabdbe9_l3.png)
Чтобы вычислить x по правилу Крамера, мы меняем первый столбец определителя матрицы A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle\bm{x} = \cfrac{\begin{vmatrix} 2 & 1 & 2\\[1.1ex]0&m&2 \\[1.1ex] 4 & 0 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{2m^2+8-8m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b17f49436fdadbb014011b5c461a4a56_l3.png)
Чтобы вычислить y по правилу Крамера, мы заменим второй столбец определителя A на столбец независимых членов и разделим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 0 & 2 \\[1.1ex] 3 & 4 & m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-4+2m}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a2bf75bdabfb2c83870f1869ce19e3d_l3.png)
Чтобы вычислить z по правилу Крамера, мы меняем третий столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & m & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-2m+4}{m^2-5m+6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eebb3c4d280afc8a9aed8877ddcd4ac5_l3.png)
Следовательно, решение системы уравнений для случая m≠3 и m≠2 имеет вид:
![]()
Как видите, в этом случае решение системы уравнений является функцией m.
Как только мы нашли решение для случая, когда m отличается от 2 и 3, мы решим систему для случая, когда m равно 2:
м=2:
Теперь мы будем анализировать систему, когда параметр m равен 2. В этом случае матрицы A и A’ имеют вид:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 2 & 2 \\[1.1ex] 3 & 0 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 2 & 2 & 0 \\[1.1ex] 3 & 0 & 2 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f42ec4801f3e84cd44b4e0b2ae6351cf_l3.png)
Как мы видели ранее, при m=2 определитель матрицы A равен 0. Следовательно, матрица A не имеет ранга 3. Но внутри нее имеется 2×2 определителя, отличных от 0, например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
Итак, в данном случае ранг A равен 2 :
![]()
Зная ранг матрицы A, мы вычисляем ранг A’. Определитель первых трех столбцов дает 0, поэтому мы пробуем другие возможные определители 3×3 в матрице A’:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 0 & 2 & 4 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 2 & 4 \end{vmatrix}=0\qquad \begin{vmatrix} 1 & 1 & 2 \\[1.1ex] -1 & 2 & 0 \\[1.1ex] 3 & 0 & 4\end{vmatrix}=0](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c68c742cae37c52ad2566b7feec5301_l3.png)
Все возможные определители размерности 3×3 дают 0. Но, очевидно, матрица A’ имеет тот же определитель 2×2, отличный от 0, что и матрица A:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 2 \end{vmatrix} = 2 - (-1)=3 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-55ef6cd148fca7a869e14760007e1f2e_l3.png)
Следовательно, матрица A’ также имеет ранг 2 :
![]()
Итак, поскольку ранг матрицы A равен рангу матрицы A’, но эти два меньше числа неизвестных системы (3), мы знаем по теореме Руше-Фробениуса , что это неопределенно совместимая система. (ИКС):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96868a2569ea0ab5ca99d8dc606d3dc9_l3.png)
Поскольку это АСУ ТП, нам необходимо преобразовать систему для ее решения. Для этого нам необходимо сначала исключить уравнение из системы, в этом случае мы удалим последнее уравнение:
![Rendered by QuickLaTeX.com \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \\[1.5ex] \cancel{3x+2z = 4} \end{cases} \longrightarrow \quad \begin{cases} x+y+2z= 2 \\[1.5ex] -x+2y+2z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10c7facda35cb8894e6bbb236e4953f1_l3.png)
Теперь преобразуем переменную z в λ:
![Rendered by QuickLaTeX.com \begin{cases}x+y+2z= 2 \\[1.5ex] -x+2y+2z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+y+2\lambda= 2 \\[1.5ex] -x+2y+2\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0155083595420da31a486927e953805c_l3.png)
И члены с λ ставим с независимыми членами:
![Rendered by QuickLaTeX.com \begin{cases}x+y=2-2\lambda \\[1.5ex] -x+2y=-2\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8486baee4be39f417988ee12b5e67c7_l3.png)
Следовательно, матрица A и матрица A’ системы остаются:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 1 \\[1.1ex] -1 & 2 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 1 & 2 -2\lambda \\[1.1ex] -1 & 2 & -2\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8591e8c21bce2f49998311bbb08f7dee_l3.png)
Наконец, преобразовав систему, мы применяем правило Крамера . Для этого сначала решим определитель А:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 1 \\[1.1ex] -1 & 2\end{vmatrix} =2-(-1)=3](https://mathority.org/wp-content/ql-cache/quicklatex.com-c34669d7234c9736c350f793df337bd3_l3.png)
Чтобы вычислить x по правилу Крамера, мы заменим первый столбец определителя A на столбец независимых членов и разделим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 -2\lambda & 1 \\[1.1ex] -2\lambda & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{4-4\lambda-(-2\lambda)}{3} = \cfrac{\bm{4-2\lambda}}{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-987ebe052154332042afeb27535996f1_l3.png)
Чтобы вычислить y по правилу Крамера, мы заменим второй столбец определителя A на столбец независимых членов и разделим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 2 -2\lambda \\[1.1ex] -1 & -2\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}}=\cfrac{-2\lambda -(-2+2\lambda)}{3} = \cfrac{\bm{2-4\lambda} }{\bm{3}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8a3c7b2cd7319f7f9db6df7df79abb50_l3.png)
Итак, при m=2 решение системы уравнений является функцией λ, поскольку она является СКИ и, следовательно, имеет бесконечные решения:
![]()
Мы уже анализировали решение системы, когда параметр m отличен от 2 и 3, а также когда он равен 2. Поэтому нам нужен только последний случай: когда m принимает значение 3:
м=3:
Теперь мы проанализируем, что происходит, когда параметр m равен 3. В этом случае матрицы A и A’ имеют вид:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc}1 & 1 & 2 \\[1.1ex] -1 & 3 & 2 \\[1.1ex] 3 & 0 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 1 & 2 & 2 \\[1.1ex] -1 & 3 & 2 & 0 \\[1.1ex] 3 & 0 & 3 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49bbc0d7d36606aa59be050c2682de5_l3.png)
Как мы видели ранее, при m=3 определитель A равен 0. Таким образом, матрица A не имеет ранга 3. Но внутри нее есть 2×2 определителя, отличных от 0, например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}1 & 1 \\[1.1ex] -1 & 3 \end{vmatrix} = 3 - (-1)=4 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-d88ce42feb4bba9aa74aae98e1062c4a_l3.png)
Итак, в данном случае ранг A равен 2 :
![]()
Зная ранг матрицы A, мы вычисляем ранг A’. Определитель первых трех столбцов дает 0, поэтому мы пробуем другой определитель 3×3, который находится внутри матрицы A’, например, определитель последних трех столбцов:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1 & 2 & 2 \\[1.1ex] 3 & 2 & 0 \\[1.1ex] 0 & 3 & 4\end{vmatrix}=2](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e6f1a5c155ca004c73e51bdcbe5ece9_l3.png)
С другой стороны, матрица A’ содержит определитель, результат которого отличен от 0, поэтому матрица A’ имеет ранг 3 :
![]()
Таким образом, при m = 3 ранг матрицы A ниже ранга матрицы A’. Таким образом, из теоремы Руше-Фробениуса мы делаем вывод, что система является несовместимой системой (НС) :
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas}=3\end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A)=2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3454f804b63f3cca9bcf08bc93815f90_l3.png)
Следовательно, система уравнений не имеет решения при m = 3.
Краткое изложение примера:
Как мы видели, решение системы уравнений зависит от значения параметра m . Вот краткое описание всех возможных случаев:
- м≠3 и м≠2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCD} \longrightarrow \begin{cases} x = \cfrac{2m^2+8-8m}{m^2-5m+6} \\[3.5ex] y =\cfrac{-4+2m}{m^2-5m+6} \\[3.5ex] z = \cfrac{-2m+4}{m^2-5m+6} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf366a55bd307517f94fd8aa00cdf598_l3.png)
- м=2:
![Rendered by QuickLaTeX.com \displaystyle \bm{SCI} \longrightarrow \begin{cases} x = \cfrac{4-2\lambda}{3} \\[3.5ex] y= \cfrac{2-4\lambda}{3} \\[3.5ex] z = \lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-94002d4f4d866569ed7d6993dd977b81_l3.png)
- м=3:
![]()
Система не имеет решения.
Здесь мы проделали весь процесс, используя теорему Руша и правило Крамера, но системы уравнений с параметрами также можно обсуждать и решать методом Гаусса (с упражнениями) . Вы можете узнать больше об этом методе на связанной странице, где вы найдете подробное объяснение процедуры, а также примеры и пошаговые решения упражнений.
Решенные дискуссионные задачи систем линейных уравнений с параметрами
Упражнение 1
Обсудите и решите следующую систему линейных уравнений, зависящих от параметров:
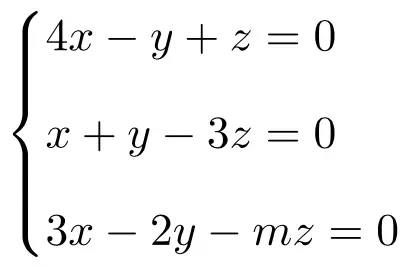
Сначала мы создаем матрицу A и расширенную матрицу A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b641845325965882d4aac899246cffb3_l3.png)
Теперь мы должны найти ранг матрицы А. Для этого проверяем, отличен ли определитель всей матрицы от 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{vmatrix} & =-4m+9-2-3-24-m \\ & =-5m-20 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d36c7cffe0248a2f45cd5871abc6ed5_l3.png)
Результат определителя A зависит от значения m. Поэтому мы увидим, при каких значениях m определитель обращается в нуль. Для этого приравниваем полученный результат к 0 и решаем уравнение:
![]()
![]()
![]()
Итак, когда m равно -4, определитель A будет 0. А когда m отличается от -4, определитель A будет отличен от 0. Поэтому мы должны анализировать каждый случай отдельно:
м≠-4:
Как мы только что видели, когда параметр m отличается от -4, определитель матрицы A отличен от 0. Следовательно, ранг матрицы A равен 3.
![]()
Более того, ранг матрицы А’ тоже равен 3, поскольку внутри нее есть подматрица размера 3×3, определитель которой отличен от 0. И она не может иметь ранга 4, поскольку «мы не можем составить определитель 4×4.
![]()
Следовательно, применяя теорему Руше-Фробениуса, мы знаем, что это совместимая детерминированная система (SCD), поскольку диапазон A равен диапазону A’ и числу неизвестных.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Как только мы узнаем, что система представляет собой SCD, мы применим правило Крамера для ее решения. Для этого напомним, что матрица А, ее определитель и матрица А’ равны:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & -m & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9e0bd352ad7713a03824ead1239041c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & -m\end{vmatrix} =-5m-20](https://mathority.org/wp-content/ql-cache/quicklatex.com-530cb4576ee1a91d6246ed6cf9dd0fc8_l3.png)
Чтобы вычислить xatex] по правилу Крамера, мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 0 & -1 & 1 \\[1.1ex] 0 & 1 & -3 \\[1.1ex] 0 & -2 & -m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b076bbda8d086abedb459570d74c80a9_l3.png)
Чтобы вычислить неизвестное по правилу Крамера, мы меняем второй столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & 0 & 1 \\[1.1ex] 1 & 0 & -3 \\[1.1ex] 3 & 0 & -m \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f642a8cb2fd174e5c383a4df53e11a2e_l3.png)
Чтобы вычислить z по правилу Крамера, мы меняем третий столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-5m-20} = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5020a9ba4995b9715d8d1fb4720952b1_l3.png)
Следовательно, решение системы уравнений для случая m≠-4 имеет вид:
х=0 у=0 z=0
м=-4:
Теперь мы проанализируем систему, когда параметр m равен -4. В этом случае матрицы A и A’ имеют вид:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 & 1 \\[1.1ex] 1 & 1 & -3 \\[1.1ex] 3 & -2 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}4 & -1 & 1 & 0 \\[1.1ex] 1 & 1 & -3 & 0 \\[1.1ex] 3 & -2 & 4 & 0\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e585e6465d27ea27ccc2c1a6ec1fe9ae_l3.png)
Как мы видели ранее, при m=-4 определитель A равен 0. Итак, матрица A не имеет ранга 3. Но внутри нее есть 2×2 определителя, отличных от 0, например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
Поскольку матрица имеет определитель порядка 2, отличный от 0, матрица A имеет ранг 2:
![]()
Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых трех столбцов дает 0, поэтому пробуем другие возможные определители 3×3:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] -2 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & 1 & 0 \\[1.1ex] 1 & -3 & 0 \\[1.1ex] 3 & 4 & 0 \end{vmatrix} = 0 \quad \begin{vmatrix}4 & -1 & 0 \\[1.1ex] 1 & 1 & 0 \\[1.1ex] 3 & -2 & 0\end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-39fc49c7a63920c8956703a4851ecfc0_l3.png)
Все определители 3×3 матрицы A’ равны 0, поэтому матрица A’ также не будет иметь ранг 3. Однако внутри него есть определители порядка 2, отличного от 0. Например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} =4-(-1)=5 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-a62d150aef4ec798814d25c988b0afd7_l3.png)
Таким образом, матрица A’ будет иметь ранг 2:
![]()
Размер матрицы A равен размеру матрицы A’, но эти два меньше числа неизвестных в системе (3), поэтому, согласно теореме Руше-Фробениуса, c представляет собой неопределенную совместимую систему (ICS):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f43fdf4978386c61d18f9bb5b5883881_l3.png)
Это система ICS, поэтому нам необходимо преобразовать систему для ее решения. Устраним сначала одно уравнение, которое в данном случае будет последним:
![Rendered by QuickLaTeX.com \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0 \\[1.5ex] \cancel{3x-2y+4z = 0} \end{cases} \longrightarrow \quad \begin{cases} 4x-y+z= 0 \\[1.5ex] x+y-3z=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d5499fda37d3cbf56fbf6ecbfc6bfba_l3.png)
Теперь преобразуем переменную z в λ:
![Rendered by QuickLaTeX.com \begin{cases}4x-y+z= 0 \\[1.5ex] x+y-3z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 4x-y+\lambda= 0 \\[1.5ex] x+y-3\lambda=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-96ea68274b072531365282e01d926718_l3.png)
И члены с λ ставим с независимыми членами:
![Rendered by QuickLaTeX.com \begin{cases} 4x-y=-\lambda \\[1.5ex] x+y=3\lambda \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6192715e62cc8e3d3fe4c51da8629c70_l3.png)
Такого, что матрица A и матрица A’ системы остаются:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 4 & -1 \\[1.1ex] 1 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 4 & -1 & -\lambda \\[1.1ex] 1 & 1 & 3\lambda \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-99a91208ff1742f81e799aa5ab7f9097_l3.png)
Наконец, преобразовав систему, мы применяем правило Крамера. Для этого сначала решим определитель А:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 4 & -1 \\[1.1ex] 1 & 1 \end{vmatrix} = 4-(-1)=5](https://mathority.org/wp-content/ql-cache/quicklatex.com-34832b783ddaf4af205302240d0feafb_l3.png)
Чтобы вычислить x по правилу Крамера, мы заменим первый столбец определителя A на столбец независимых членов и разделим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix}-\lambda & -1 \\[1.1ex] 3\lambda & 1 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-\lambda-(-3\lambda)}{5} =\cfrac{\bm{2\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-362167d2eaa02d7243dedd5c385d08b1_l3.png)
Чтобы вычислить неизвестное по правилу Крамера, мы меняем второй столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} 4 & -\lambda \\[1.1ex] 1 & 3\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12\lambda-(-\lambda)}{5}=\cfrac{\bm{13\lambda}}{\bm{5}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ede5a3a87ac0bb9ceea4232ec7b381fd_l3.png)
Итак, при m=-4 решение системы уравнений является функцией λ, поскольку она является SCI и, следовательно, имеет бесконечные решения:
![]()
Упражнение 2
Обсудите и найдите решение следующей системы линейных уравнений, зависящих от параметров:
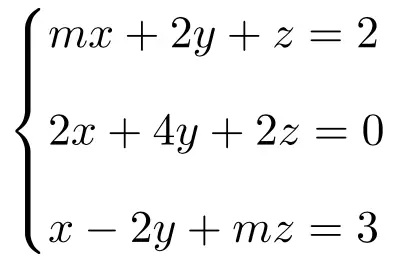
Первое, что нужно сделать, это матрица A и расширенная матрица A’ системы:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
Теперь мы должны найти ранг матрицы А. Для этого проверяем, отличен ли определитель всей матрицы от 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix} & =4m^2+4-4-4+4m-4m \\ & =4m^2-4 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d0f8dbb7408ac6521e0144ac2f3a8a3_l3.png)
Результат определителя A зависит от значения m. Поэтому мы увидим, при каких значениях m определитель обращается в нуль. Для этого приравниваем полученный результат к 0 и решаем уравнение:
![]()
![]()
![]()
![]()
![]()
Итак, когда m равно +1 или -1, определитель A будет 0. А когда m отличается от +1 и -1, определитель A будет отличаться от 0. Поэтому мы должны проанализировать каждый случай следующим образом:
м≠+1 и м≠-1:
Как мы только что видели, когда параметр m отличается от +1 и -1, определитель матрицы A отличен от 0. Следовательно, ранг матрицы A равен 3.
![]()
Более того, ранг матрицы А’ тоже равен 3, поскольку внутри нее есть подматрица размера 3×3, определитель которой отличен от 0. И она не может иметь ранга 4, поскольку «мы не можем составить определитель 4×4.
![]()
Следовательно, применяя теорему Руше-Фробениуса, мы знаем, что это совместимая детерминированная система (SCD), поскольку диапазон A равен диапазону A’ и числу неизвестных.
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31b495a48a75d7af1f23e38818bf4eca_l3.png)
Как только мы узнаем, что система представляет собой SCD, мы применим правило Крамера для ее решения. Для этого напомним, что матрица А, ее определитель и матрица А’ равны:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}m & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & m & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-e924dd1b3fe5c0da561b92da9bf5da3b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}m & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & m\end{vmatrix}=4m^2-4](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5114be5e37d2c91f02f22fba22edc42_l3.png)
Чтобы вычислить x по правилу Крамера, мы меняем первый столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2& 2 & 1 \\[1.1ex] 0 & 4 & 2 \\[1.1ex] 3 & -2 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{8m+8}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b7402e02ee62bd78a6f880d3d122119_l3.png)
Чтобы вычислить неизвестное по правилу Крамера, мы меняем второй столбец определителя A на столбец независимых членов и делим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{y} = \cfrac{\begin{vmatrix} m & 2 & 1 \\[1.1ex] 2 & 0 & 2 \\[1.1ex] 1 & 3 & m\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{-10m+10}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-551c66a9530d0195a9a4ff64d42350c4_l3.png)
Чтобы вычислить z по правилу Крамера, мы заменим третий столбец определителя A на столбец независимых членов и разделим его на определитель A:
![Rendered by QuickLaTeX.com \displaystyle \bm{z} = \cfrac{\begin{vmatrix}m & 2 & 2 \\[1.1ex] 2 & 4 & 0 \\[1.1ex] 1 & -2 & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{\bm{12m-28}}{\bm{4m^2-4}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-28375ce522b7644a745a9adea4c78ae7_l3.png)
Следовательно, решение системы уравнений для случая m≠+1 и m≠-1 имеет вид:
![]()
м=+1:
Теперь мы будем анализировать систему, когда параметр m равен 1. В этом случае матрицы A и A’ имеют вид:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & 1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6af272a99ed7c281ee8dd9199698686_l3.png)
Как мы видели ранее, когда m=+1 определитель A равен 0. Таким образом, матрица A не имеет ранга 3. Но внутри нее есть 2×2 определителя, отличных от 0, например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}2 & 4\\[1.1ex] 1 & -2 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ebedf6c9e4316844dc99ceca9472fac5_l3.png)
Поскольку матрица имеет определитель порядка 2, отличный от 0, матрица A имеет ранг 2:
![]()
Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых 3-х столбцов дает 0, поэтому теперь попробуем, например, с определителем последних 3-х столбцов:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2 & 1 & 2 \\[1.1ex] 4 & 2 & 0 \\[1.1ex] -2 & 1 & 3 \end{vmatrix} = 16](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d0109b155be9f87a0cee337ddec5517_l3.png)
С другой стороны, матрица A’ содержит определитель 3×3, результат которого отличен от 0, так что матрица A’ имеет ранг 3:
![]()
Таким образом, когда m=+1, ранг матрицы A меньше ранга матрицы A’. Таким образом, из теоремы Руше-Фробениуса мы делаем вывод, что система является несовместимой системой (НС):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
Следовательно, система уравнений не имеет решения при m=+1 , так как это несовместная система.
м=-1:
Теперь мы проанализируем систему, когда параметр m равен -1. В этом случае матрицы A и A’ имеют вид:
![Rendered by QuickLaTeX.com \displaystyle A= \left( \begin{array}{ccc} -1 & 2 & 1 \\[1.1ex] 2 & 4 & 2 \\[1.1ex] 1 & -2 & -1 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c}-1 & 2 & 1 & 2 \\[1.1ex] 2 & 4 & 2 & 0 \\[1.1ex] 1 & -2 & -1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-46b0a00ef38d0e5a433b418de7eb1ec3_l3.png)
Как мы видели ранее, при m=-1 определитель A равен 0. Итак, матрица A не имеет ранга 3. Но внутри нее есть 2×2 определителя, отличных от 0, например:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}-1 & 2\\[1.1ex] 2 & 4 \end{vmatrix} =-4-4=-8 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ff5373c7e7901f253421efbbd52d192e_l3.png)
Поскольку матрица имеет определитель порядка 2, отличный от 0, матрица A имеет ранг 2:
![]()
Зная ранг A, мы вычисляем ранг A’. Мы уже знаем, что определитель первых 3-х столбцов дает 0, поэтому теперь пробуем, например, с определителем 1, 3 и 4 столбцов:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} -1 & 1 & 2 \\[1.1ex] 2 & 2 & 0 \\[1.1ex] 1 & -1 & 3\end{vmatrix} = -20](https://mathority.org/wp-content/ql-cache/quicklatex.com-a95e30910bd64db920f3c2bcb5f2ff62_l3.png)
С другой стороны, матрица A’ содержит определитель 3×3, результат которого отличен от 0, так что матрица A’ имеет ранг 3:
![]()
Таким образом, когда m = -1, ранг матрицы A ниже ранга матрицы A’. Таким образом, из теоремы Руше-Фробениуса мы делаем вывод, что система является несовместимой системой (НС):
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = 2 \ \neq \ rg(A') = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SI}\phantom{^9_9}} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bb3fec88cf5c6d788afb4480ab1f58_l3.png)
Следовательно, система уравнений не имеет решения при m=-1 , так как это несовместная система.