На этой странице вы узнаете, что это такое и как вычислять обратную матрицу методом определителей (или сопряженной матрицы) и методом Гаусса. Вы также увидите все свойства обратной матрицы, а также найдете пошагово решаемые примеры и упражнения для каждого метода, чтобы полностью их понять. Наконец, мы объясним формулу быстрого обращения матрицы 2×2 и даже самую большую полезность этой матричной операции: решение системы линейных уравнений.
Что такое обратная матрица?
Быть
![]()
квадратная матрица. Обратная матрица
![]()
это написано
![]()
, и именно эта матрица удовлетворяет:
![]()
![]()
Золото
![]()
это матрица идентичности.
Когда можно инвертировать матрицу, а когда нельзя?
Самый простой способ определить обратимость матрицы — использовать ее определитель:
- Если определитель рассматриваемой матрицы отличен от 0, это означает, что матрица обратима. В этом случае мы говорим, что это регулярная матрица. Кроме того, это означает, что матрица имеет максимальный ранг.
- С другой стороны, если определитель матрицы равен 0, матрицу нельзя инвертировать. И в этом случае мы говорим, что это сингулярная или вырожденная матрица.
В основном существует два метода обращения любой матрицы: метод определителей или присоединенной матрицы и метод Гаусса. Ниже вы найдете объяснение первого, но вы также можете проконсультироваться ниже, как инвертировать матрицу с помощью метода Гаусса.
Инвертируйте матрицу, используя метод определителя (или используя соседнюю матрицу)
Чтобы вычислить обратную матрицу ,
![]()
, необходимо применить следующую формулу:
![]()
Золото:
-
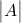
является определителем матрицы

-
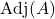
является присоединенной матрицей

- Экспонент
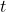
указывает на транспонирование матрицы, т.е. присоединенная матрица должна быть транспонирована.
Комментарий: В некоторых книгах используется немного другая формула обратной матрицы: сначала транспонируется матрица A, а затем вычисляется ее сопряженная матрица, вместо того, чтобы сначала вычислять сопряженную матрицу, а затем транспонировать ее. На самом деле порядок не имеет значения, поскольку результат будет точно таким же. Здесь мы оставляем вам формулу для инвертирования модифицированной матрицы на случай, если вы предпочитаете использовать ее:

Затем мы увидим , как найти обратную матрицу , решив в качестве примера упражнение:
Пример вычисления обратной матрицы методом определителя (или присоединенной матрицы):
- Вычислите обратную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
Для определения обратной матрицы необходимо применить следующую формулу:
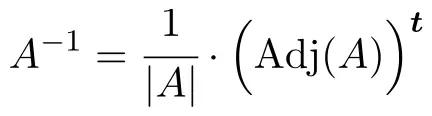
Но если определитель матрицы равен нулю, это означает, что матрица необратима. Поэтому первое, что нужно сделать, это вычислить определитель матрицы и проверить, что он отличен от 0:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{vmatrix} = -4- (-6) = 2](https://mathority.org/wp-content/ql-cache/quicklatex.com-710ccd4e4912dd492b496a742eaf7f56_l3.png)
Определитель не равен 0 , поэтому матрица обратима .
Следовательно, подставив в формулу значение определителя, обратная матрица будет равна:
![]()
![]()
Теперь мы должны вычислить заместительную матрицу A. Для этого мы должны заменить каждый элемент матрицы A его заместителем.
Помните, что для расчета вложения
![]()
, то есть элемента строки
![]()
и столбец
![]()
, необходимо применить следующую формулу:
![]()
Если дополнительный минор
![]()
– определитель матрицы, исключающий строку
![]()
и столбец
![]()
.
Таким образом, заместителями элементов матрицы А являются:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 4 & -2 \\[1.1ex] 3 & -1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c37ec4a7afd5b313bcf3c50d6ce26c6d_l3.png)
![]()
![]()
![]()
![]()
Комментарий: Не путайте определитель 1×1 с абсолютным значением, поскольку в определителе 1×1 число не преобразуется в положительное.
После расчета заместителей просто замените элементы A их заместителями, чтобы найти матрицу заместителей A :
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-08fb7666b4518399c2a469ba445762be_l3.png)
Комментарий: в некоторых местах сопряженная матрица является транспонированием сопряженной матрицы, которую мы здесь определяем.
Поэтому мы подставляем присоединенную матрицу в формулу обратной матрицы, и она становится такой:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & -3 \\[1.1ex] 2 & 4 \end{pmatrix} ^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0abb4127db9c3c1d0a7b669fbc782605_l3.png)
Экспонент
![]()
Это говорит нам о том, что нам нужно транспонировать матрицу . И чтобы транспонировать матрицу, вам нужно преобразовать ее строки в столбцы , то есть первая строка матрицы становится первым столбцом матрицы, а вторая строка становится вторым столбцом:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{2} \cdot \begin{pmatrix} -1 & 2 \\[1.1ex] -3 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-22965912cf8aee99610c81cf575c0ecd_l3.png)
И, наконец, мы умножаем каждый член матрицы на
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{-1}{2} & \sfrac{2}{2} \\[1.1ex] \sfrac{-3}{2} & \sfrac{4}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-220748840151b429919c7ce6587b1bc0_l3.png)
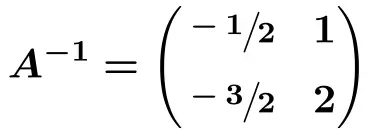
Решаемые упражнения на обратные матрицы методом определителей (или присоединенной матрицы)
Упражнение 1
Инвертируйте следующую матрицу размерности 2×2, используя метод сопряженной матрицы:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfb0807249e78845b375a402eb23a32b_l3.png)
Формула обратной матрицы:
![]()
Сначала вычислим определитель матрицы:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 1 & 3 \\[1.1ex] 2 & 7 \end{vmatrix} = 7-6 = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c4e3bac90eb0da0361b4be1a2225146_l3.png)
Определитель отличен от 0, поэтому матрицу можно инвертировать.
Теперь вычислим сопряженную матрицу A:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dea8fca2c025ff9b7d7673904344996_l3.png)
После того как определитель матрицы и сопряженный к ней вычислены, подставляем их значения в формулу:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{1} \cdot \begin{pmatrix} 7 & -2 \\[1.1ex] -3 & 1 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9475e4162eff7e1ed9c08f363a8279ec_l3.png)
Транспонируем прикрепленную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = 1 \cdot \begin{pmatrix} 7 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a6aaa8168e55c6eab1e3be1229a3da_l3.png)
Таким образом, обратная матрица A равна:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{7} & \bm{-3} \\[1.1ex] \bm{-2} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1236ad7262705dbbd9b0a094084ceac5_l3.png)
Упражнение 2
Инвертируйте следующую квадратную матрицу, используя метод определителя:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -3 & -2 \\[1.1ex] 5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb735917d200ed35918cd44be6bd155b_l3.png)
Формула обратной матрицы:
![]()
Сначала вычислим определитель матрицы:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} -3 & -2 \\[1.1ex] 5 & 4\end{vmatrix} = -12+10 = -2](https://mathority.org/wp-content/ql-cache/quicklatex.com-49cd3daf7c50c811e78c29efe036bda4_l3.png)
Определитель отличен от 0, поэтому матрицу можно инвертировать.
Теперь вычислим сопряженную матрицу A:
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-208ab7161076485ca6928bd1208f6714_l3.png)
После того как определитель матрицы и сопряженный к ней найден, подставляем их значения в формулу:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & -5 \\[1.1ex] 2 & -3 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-babecc87455bdc54006a77ba5369e540_l3.png)
Транспонируем прикрепленную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{-2} \cdot \begin{pmatrix} 4 & 2 \\[1.1ex] -5 & -3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-17529597656a112a27d136ca212834d8_l3.png)
Умножаем каждый элемент на
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{4}{-2} & \cfrac{2}{-2} \\[3ex] \cfrac{-5}{-2} & \cfrac{-3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-be52d2df839244cbb0b0ee00c9e45265_l3.png)
Таким образом, обратная матрица A равна:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \bm{-2} & \bm{-1} \\[2ex] \cfrac{\bm{5}}{\bm{2}} & \cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13e218c7d075daba3f875345f324d001_l3.png)
Упражнение 3
Инвертируйте следующую матрицу размером 3×3, используя метод сопряженной матрицы:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1b6a5f638281754d80983b5a50e15be_l3.png)
Формула обратной матрицы:
![]()
Сначала решаем определитель матрицы по правилу Сарруса:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 2&3&-2\\[1.1ex] 1&4&1\\[1.1ex] 2&1&-3 \end{vmatrix} = -24+6-2+16-2+9 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcac1cb3935b1000b6493a2866e8728a_l3.png)
Определитель отличен от 0, поэтому матрицу можно инвертировать.
Решив определитель, находим сопряженную матрицу A:
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 4&1\\[1.1ex] 1&-3 \end{vmatrix} = 1 \cdot (-13) = \bm{-13}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c510482ac77a8c5d511c095de600f1ba_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 3} = \displaystyle (-1)^{1+2} \bm{\cdot} \begin{vmatrix}1&1\\[1.1ex] 2&-3\end{vmatrix} = -1 \cdot (-5) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fa99e03d34c925098c1ad3ed6f06c745_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -2} = \displaystyle (-1)^{1+3} \bm{\cdot} \begin{vmatrix} 1&4\\[1.1ex] 2&1 \end{vmatrix} = 1\cdot (-7) = \bm{-7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3bf9f8565b3e4a99ff254c7558699c13_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 3&-2 \\[1.1ex] 1&-3 \end{vmatrix} = -1 \cdot (-7) = \bm{7}](https://mathority.org/wp-content/ql-cache/quicklatex.com-99e2c3f55fbba7b5faa014758b60f4a8_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 4} = \displaystyle (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 2&-3 \end{vmatrix} = 1 \cdot (-2) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-23326bccecf752508e7418cbbc8eacd3_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 2&1\end{vmatrix} = -1 \cdot (-4) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9d056af07ce26751783152a67cdedb6_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 2} = \displaystyle (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 3&-2\\[1.1ex] 4&1\end{vmatrix} = 1 \cdot 11 = \bm{11}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bed501806c35c94e491ad2063b2d0653_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de 1} = \displaystyle (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 2&-2\\[1.1ex] 1&1\end{vmatrix} = -1 \cdot 4 = \bm{-4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3f108a61eec662b9420708f6920060be_l3.png)
![Rendered by QuickLaTeX.com \text{Adjunto de -3} = \displaystyle (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 2&3\\[1.1ex] 1&4 \end{vmatrix} = 1 \cdot 5 = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-77a152a00dbb5f1e0f8702dd9511095a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b4642a75697fd30286065cdb4063a7bd_l3.png)
После того как мы вычислили определитель матрицы и сопряженный к ней, подставляем их значения в формулу:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 5 & -7 \\[1.1ex] 7 & -2 & 4 \\[1.1ex] 11 & -4 & 5 \end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fae003a07d40b69690566cde77857c3a_l3.png)
Транспонируем прикрепленную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} -13 & 7 & 11 \\[1.1ex] 5 & -2 & -4 \\[1.1ex] -7 & 4 & 5 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55717407766afe98f50ca75f20536edc_l3.png)
И инвертированная матрица A:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =} \begin{pmatrix} \sfrac{\bm{-13}}{\bm{3}} & \sfrac{\bm{7}}{\bm{3}} & \sfrac{\bm{11}}{\bm{3}} \\[1.1ex] \sfrac{\bm{5}}{\bm{3}} & \sfrac{\bm{-2}}{\bm{3}} & \sfrac{\bm{-4}}{\bm{3}} \\[1.1ex] \sfrac{\bm{-7}}{\bm{3}} & \sfrac{\bm{4}}{\bm{3}} & \sfrac{\bm{5}}{\bm{3}}\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9835713a5b791ee959d6571d706180f3_l3.png)
Упражнение 4
Инвертируйте следующую матрицу порядка 3, используя метод сопряженной матрицы:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf71320b51e9514d1c372389aeb3410a_l3.png)
Формула обратной матрицы:
![]()
Сначала нам нужно вычислить определитель матрицы, потому что, если определитель равен 0, это означает, что матрица не имеет обратной.
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}A\end{vmatrix}=\begin{vmatrix} 4&5&-1\\[1.1ex] -1&3&2\\[1.1ex] 3&8&1 \end{vmatrix} = 12+30+8+9-64+5 = \bm{0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb7dc647f4121450eeadf2f5b62b4475_l3.png)
Определитель A равен 0, поэтому матрицу нельзя инвертировать.
Упражнение 5
Инвертируйте следующую квадратную матрицу 3 × 3 методом определительной матрицы:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-92e56e0f8013b6b65c0894a139537cae_l3.png)
Формула обратной матрицы:
![]()
Прежде всего решаем определитель матрицы по правилу Саррюса:
![Rendered by QuickLaTeX.com \displaystyle \lvert A \rvert = \begin{vmatrix} 1 & 4 & -3 \\[1.1ex] -2 & 1 & 0 \\[1.1ex] -1 & -2 & 2 \end{vmatrix} = 2+0-12-3-0+16 = 3](https://mathority.org/wp-content/ql-cache/quicklatex.com-07f116ed906c31644ed0513667988e6f_l3.png)
Определитель отличен от 0, поэтому матрицу можно инвертировать.
Решив определитель, находим сопряженную матрицу A:
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{1+1} \bm{\cdot} \begin{vmatrix} 1 & 0 \\[1.1ex] -2 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-0) = \bm{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-20da2eac0d49b1134b39b1f5c95c5659_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 4} = (-1)^{1+2} \bm{\cdot} \begin{vmatrix} -2 & 0 \\[1.1ex] -1 & 2 \end{vmatrix} = -1 \bm{\cdot} (-4-0) = \bm{4}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c5b80624f0963dfb1a111d96b4e1ceae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -3} = (-1)^{1+3} \bm{\cdot} \begin{vmatrix} -2 & 1 \\[1.1ex] -1 & -2 \end{vmatrix} = 1 \bm{\cdot} \bigl(4-(-1)\bigr) = \bm{5}](https://mathority.org/wp-content/ql-cache/quicklatex.com-50dd371e77d1896adb197321b68efd1d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{2+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] -2 & 2 \end{vmatrix} = -1 \bm{\cdot} (8-6) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-60b779f4366a3ef38ae522fcfca8e7d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 1} = (-1)^{2+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -1 & 2 \end{vmatrix} = 1 \bm{\cdot} (2-3) = \bm{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51cb00c42e6932810a4220eb85c61acd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 0} = (-1)^{2+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -1 & -2 \end{vmatrix} = -1 \bm{\cdot} \bigl(-2-(-4)\bigr) = \bm{-2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3b26cbfa55d5567d2dae10c5dfbd158_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -1} = (-1)^{3+1} \bm{\cdot} \begin{vmatrix} 4 & -3 \\[1.1ex] 1 & 0 \end{vmatrix} = 1 \bm{\cdot} \bigl(0-(-3)\bigr) = \bm{3}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d9f1bf4f5e01df910cd59bd4b25f816_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de -2} = (-1)^{3+2} \bm{\cdot} \begin{vmatrix} 1 & -3 \\[1.1ex] -2 & 0 \end{vmatrix} = -1 \cdot (0-6) = \bm{6}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ce129b17734facf076e48fb1928d0e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \text{Adjunto de 2} = (-1)^{3+3} \bm{\cdot} \begin{vmatrix} 1 & 4 \\[1.1ex] -2 & 1 \end{vmatrix} = 1 \bm{\cdot} \bigl(1-(-8)\bigr) = \bm{9}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3c8b319461dad7880bf2b9f20187b6fb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \displaystyle \text{Adj}(A) = \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-748fcb9d9d2a8326379da4d2bd08534a_l3.png)
После того как мы вычислили определитель матрицы и сопряженный к ней, подставляем их значения в формулу:
![]()
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & 4 & 5 \\[1.1ex] -2 & -1 & -2 \\[1.1ex] 3 & 6 & 9\end{pmatrix}^{\bm{t}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3a0fc0e6effb520e22ff82c3034b4d4c_l3.png)
Транспонируем прикрепленную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \cfrac{1}{3} \cdot \begin{pmatrix} 2 & -2 & 3 \\[1.1ex] 4 & -1 & 6 \\[1.1ex] 5 & -2 & 9 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bba6ddbc8ab9f2c64eb03cdb9fea530a_l3.png)
И наконец, мы работаем:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \sfrac{2}{3} & \sfrac{-2}{3} & \sfrac{3}{3} \\[1.1ex] \sfrac{4}{3} & \sfrac{-1}{3} & \sfrac{6}{3} \\[1.1ex] \sfrac{5}{3} & \sfrac{-2}{3} & \sfrac{9}{3} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41f999c23e7d5ce129b410b9f486983e_l3.png)
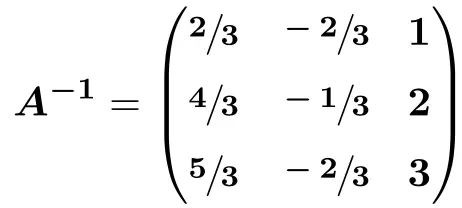
Инвертируйте матрицу с помощью метода Гаусса:
Чтобы вычислить обратную матрицу методом Гаусса , необходимо выполнить операции над строками матрицы (это мы увидим позже). Поэтому, прежде чем узнать, как использовать метод Гаусса, важно знать все операции, которые можно выполнять со строками матриц:
Преобразования линий, разрешенные в методе Гаусса
- Измените порядок строк матрицы.
Например, мы можем изменить порядок строк 2 и 3 матрицы:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] -2 & 4 & -1 \\[2ex] 6 & 1 & -3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc} 3 & 5 & -2 \\[2ex] 6 & 1 & -3 \\[2ex] -2 & 4 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d3f607625afb96bfb250168bd330818_l3.png)
- Умножьте или разделите все члены подряд на число, отличное от 0.
Например, мы можем умножить строку 1 на 4 и разделить строку 3 на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} 1 & -2 & 3 \\[2ex] 3 & -1 & 5 \\[2ex] 2 & -4 & -2 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc} 4 & -8 & 12 \\[2ex] 3 & -1 & 5 \\[2ex] 1 & -2 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cca4df71c23b1f005068a0a93b77dfe_l3.png)
- Замените строку суммой той же строки плюс другой строки, умноженной на число.
Например, в следующей матрице мы добавляем строку 3, умноженную на 1, к строке 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 2 & 4 & 1 \\[2ex] 1 & -2 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1\cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc} -1 & -3 & 4 \\[2ex] 3 & 2 & 4 \\[2ex] 1 & -2 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ca6644f015dd42ddbf4ab159bd10dec_l3.png)
Пример расчета обратной матрицы методом Гаусса:
Давайте посмотрим на примере, как применить метод Гаусса для инвертирования матрицы:
- Вычислите обратную матрицу:
![Rendered by QuickLaTeX.com \displaystyle A = \left( \begin{array}{ccc} 1 & 0 & 1 \\[2ex] 0 & 2 & 1 \\[2ex] 1 & 5 & 4 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-71553480cefa679dcb8eb98d97e0c717_l3.png)
Первое, что нам нужно сделать, это объединить матрицу A и матрицу Identity в одну матрицу . Матрица A слева и матрица идентичности справа:
![]()
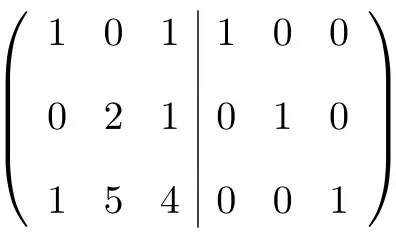
Чтобы вычислить обратную матрицу, нам нужно преобразовать левую матрицу в единичную матрицу. И для этого нам нужно применять преобразования к строкам, пока мы не доберемся до нужного результата.
Мы будем действовать по столбцам, то есть будем выполнять операции над строками, чтобы сначала преобразовать числа в первом столбце, затем во втором столбце и, наконец, в третьем столбце.
1 и 0 в первом столбце уже подходят, поскольку единичная матрица также имеет 1 и 0 на этих позициях. Поэтому на данный момент нет необходимости применять преобразование к этим строкам.
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} \color{blue}\boxed{\color{black}1} & 0 & 1 & 1 & 0 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-7f51b3a869dde9c1697be9e57fce1548_l3.png)
Однако единичная матрица имеет 0 в последнем элементе первого столбца, где теперь у нас есть 1. Поэтому нам нужно преобразовать 1 в 0. Для этого мы добавляем строку 1, умноженную на –, к строке 3.1:

Итак, если мы сделаем эту сумму, мы получим следующую матрицу:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] \color{blue}\boxed{\color{black}0} & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-992a31603c2182a97d31ddf787df4f06_l3.png)
Таким образом, нам удалось превратить 1 в 0.
Теперь перейдем ко второму столбцу левой матрицы. Первый элемент — это 0, и это хорошо, поскольку единичная матрица имеет 0 в той же позиции. Однако вместо 2 должна быть 1, поэтому делим вторую строку на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 2 & 1 & 0 & 1 & 0 \\[2ex] 1 & 5 & 4 &0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/2}\\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}1} & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a86b61ee601f9cd0ff9a70d1a280f887_l3.png)
Кроме того, во втором столбце нам также нужно превратить 5 в 0. Ну, поскольку 5 в пять раз больше, чем 1 во второй строке, мы добавим строку 2, умноженную на -5, к строке 3:

Следовательно, выполнив эту операцию, мы получим матрицу с 0 в последнем элементе второго столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 5 & 3 & -1 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 5f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-fcc790f05d73d308cb7d992841ab031a_l3.png)
Наконец, мы преобразуем последний столбец матрицы влево, но на этот раз мы должны начать снизу. Поэтому необходимо преобразовать
![]()
в 1. Поэтому умножаем последнюю строку на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \sfrac{1}{2} & -1 & \sfrac{-5}{2} & 1 \end{array} \right)\begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & \color{blue}\boxed{\color{black}1} & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-69614cae4dd388b6454ffd9b8d63c9a5_l3.png)
Теперь мы должны преобразовать
![]()
оставшаяся часть последнего столбца равна 0. Однако на этот раз мы не можем умножить строку на 2, потому что мы также преобразуем 1 в 2 (когда единичная матрица имеет 1 в этой позиции). Поэтому к строке 2 добавим строку 3, разделенную на -2:

Итак, проделав эту операцию, нам удалось преобразовать
![]()
в 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{1}{2} & 0 & \sfrac{1}{2} & 0 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & \color{blue}\boxed{\color{black}0} & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-537958a51f67c7602ef121fa2c997ca8_l3.png)
Наконец, нам просто нужно преобразовать 1 в первой строке третьего столбца в 0. В третьей строке также есть 1 в том же столбце, поэтому мы добавим строку 3, умноженную на -1, к строке 1:
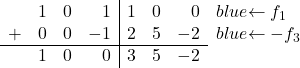
И выполнив эту операцию, нам удалось преобразовать 1 в 0:
![Rendered by QuickLaTeX.com \ \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 &0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & \color{blue}\boxed{\color{black}0} & 3 & 5 & -2 \\[2ex] 0 & 1 & 0 & 1 & 3 & -1 \\[2ex] 0 & 0 & 1 & -2 & -5 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ddd39df6bc92258ba163c65de4fd59f_l3.png)
После того как мы успешно преобразовали левую матрицу в единичную матрицу, мы также знаем обратную матрицу. Потому что обратная матрица — это матрица, которую мы получаем в правой части, преобразуя левую матрицу в единичную матрицу . Таким образом, обратная матрица равна:
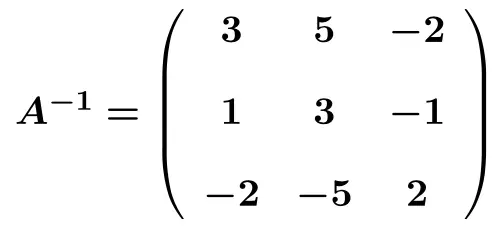
Решаемые упражнения на обратные матрицы методом Гаусса
Упражнение 1
Инвертируйте следующую матрицу с помощью метода Гаусса:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36886e1ab1007f9a53bdc0dd71a0d15b_l3.png)
Первое, что нам нужно сделать, это объединить матрицу A и матрицу Identity в одну матрицу. Матрица A слева и единичная матрица справа:
![]()
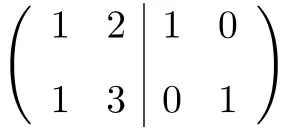
Теперь, чтобы вычислить обратную матрицу, нам нужно преобразовать левую матрицу в единичную матрицу. И для этого нам нужно применять преобразования к строкам, пока мы не доберемся до нужного результата.
Первый член всех, 1, уже такой же, как единичная матрица. Поэтому на данный момент нет необходимости применять преобразование к первой строке.
Однако единичная матрица имеет 0 в последнем элементе первого столбца, где теперь у нас есть 1. Поэтому нам нужно преобразовать 1 в 0. Для этого мы вычитаем строку 1 из строки 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc}1 & 2 & 1 & 0 \\[1.5ex] 1 & 3 & 0 & 1\end{array} \right) \begin{array}{c} \\[1.5ex] \xrightarrow{f_2 - f_1} \end{array} \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-247d8605795c43e79b5d7742854cfe6d_l3.png)
Переходим ко второму столбцу: 1 ниже – хорошо. Но не 2 выше, поскольку единичная матрица имеет 0 в этой позиции. Следовательно, чтобы преобразовать 2 в 0, из строки 1 вычитаем строку 2, умноженную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{cc|cc} 1 & 2 & 1 & 0 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - 2f_2} \\[1.5ex] & \end{array} \left( \begin{array}{cc|cc} 1 & 0 & 3 & -2 \\[1.5ex] 0 & 1 & -1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-173a7bdb55ba058e5ae16d1fd8e91564_l3.png)
Обратная матрица — это матрица, которую мы получаем в правой части после преобразования матрицы слева в единичную матрицу. И теперь мы получили единичную матрицу с левой стороны. Таким образом, обратная матрица равна:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left(} \begin{array}{cc} \bm{3} & \bm{-2} \\[1.5ex] \bm{-1} & \bm{1} \end{array}\bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-98896d28465c9e1402e1c443375d93fe_l3.png)
Упражнение 2
Инвертируйте следующую матрицу с помощью процедуры Гаусса:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 1 & -4 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 0 & 1 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ae5ba4a92a5ddc00ddf5b11775edafd_l3.png)
Сначала мы помещаем матрицу A и матрицу идентичности в одну матрицу:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-81db2ef94d2db597cebb4c0c77685526_l3.png)
Теперь нам нужно преобразовывать строки, пока мы не преобразуем левую матрицу в единичную матрицу.
Первый столбец левой матрицы уже такой же, как первый столбец единичной матрицы. Поэтому нет необходимости изменять какие-либо его номера.
Однако единичная матрица имеет 1 во втором элементе второго столбца, где теперь есть 3. Поэтому мы должны преобразовать 3 в 1. Для этого из строки 2 мы вычитаем строку 3, умноженную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 3 & 2 & 0 & 1 & 0 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - 2f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & 4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-bfd7cb4d4b81a75038807eb28393a83e_l3.png)
Единичная матрица имеет 0 в последнем элементе второго столбца, где теперь стоит 1. Поэтому мы должны преобразовать 1 в 0. Для этого мы вычитаем строку 2 из строки 3:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 1 & 1 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-932479e2f574c19ad7906d3d20e52ad0_l3.png)
Единичная матрица имеет 0 в первом элементе второго столбца, где теперь стоит 1. Поэтому мы должны преобразовать 1 в 0. Для этого мы вычитаем строку 2 из строки 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 1 & -4 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-566e1453aab03f9792cb281e4c88a68c_l3.png)
Все, что нам нужно сделать сейчас, это преобразовать -4 в 0. Для этого мы добавляем строку 3, умноженную на 4, к строке 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & -4 & 1 & -1 & 2 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3\end{array} \right) \begin{array}{c} \xrightarrow{f_1 + 4f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 1 & -5 & 14 \\[2ex] 0 & 1 & 0 & 0 & 1 & -2 \\[2ex] 0 & 0 & 1 & 0 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f98a9cabeb101602dd11aa73516b998_l3.png)
Мы уже получили единичную матрицу с левой стороны. Таким образом, обратная матрица равна:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{1} & \bm{-5} & \bm{14} \\[2ex] \bm{0} & \bm{1} & \bm{-2} \\[2ex] \bm{0} & \bm{-1 }& \bm{3} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e43ce6a7061f0339bd5d44b83afec07f_l3.png)
Упражнение 3
Инвертируйте следующую матрицу, используя метод Гаусса:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & 2 & 1 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 2 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f02b0186690e68baaa9a630db2c870db_l3.png)
Прежде чем мы начнем работать, нам нужно объединить матрицу A и матрицу Identity в одну матрицу:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa6dc5af82076e22b1d0cf7ea16d748b_l3.png)
Теперь мы должны преобразовать левую матрицу в единичную матрицу, оперируя строками.
Первые два элемента первого столбца уже такие же, как элементы единичной матрицы. Поэтому нет необходимости изменять эти цифры.
Но единичная матрица имеет 0 в третьем элементе первого столбца, где теперь есть 2. Поэтому мы должны преобразовать 2 в 0. Для этого из строки 3 мы вычитаем строку 1, умноженную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 2 & 0 & 3 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 - 2f_1} \end{array} \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-680a314b8cc900e01886291af12145e4_l3.png)
Единичная матрица имеет 0 в первом элементе второго столбца, где теперь есть 2. Поэтому мы должны преобразовать 2 в 0. Для этого из строки 1 мы вычитаем строку 2, умноженную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 2 & 1 & 1 & 0 & 0 \\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 -2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f87cbc594287f7ea4938091878562b4c_l3.png)
Единичная матрица имеет 0 в последнем элементе второго столбца, где теперь стоит -4. Поэтому мы должны преобразовать -4 в 0. Для этого мы добавляем строку 2, умноженную на 4, к строке 3:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & -4 & 1 & -2 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 +4f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8cf2c3878d2d35656953a55bb3baf94_l3.png)
Все, что нам нужно сделать сейчас, это преобразовать первый элемент третьего столбца в 0. Для этого мы добавляем к строке 1 строку 3, умноженную на -1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & 1 & -2 & 0\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1 - f_3} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc}1 & 0 & 0 & 3 & -6 & -1\\[2ex] 0 & 1 & 0 & 0 & 1 & 0 \\[2ex] 0 & 0 & 1 & -2 & 4 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-aac851b05c2dc25af3d7b9ecc622c9f6_l3.png)
Мы уже поняли, что матрица слева — это единичная матрица. Итак, обратная матрица
![]()
Восток:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{3} & \bm{-6} & \bm{-1} \\[2ex] \bm{0} & \bm{1} & \bm{0} \\[2ex] \bm{-2} & \bm{4}& \bm{1} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-161fbe4a4d4dcc4fc503b6e3a9e0bfeb_l3.png)
Упражнение 4
Инвертируйте следующую матрицу, используя метод Гаусса:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 1 & -2 & 0 \\[1.1ex] 1 & 2 & 2 \\[1.1ex] 0 & 3 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-47ad7ccd6aafab72255c96f2bc9148a2_l3.png)
Первое, что нам нужно сделать, это объединить матрицу A и матрицу Identity в одну матрицу:
![]()
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a832ceb9f09dfa88238c570b46b74d92_l3.png)
Теперь мы должны преобразовать матрицу слева в единичную матрицу, применив операции со строками.
Первый элемент первого столбца уже такой же, как у единичной матрицы. Поэтому нет необходимости его менять.
Однако единичная матрица имеет 0 во втором элементе первого столбца, где теперь стоит 1. Поэтому мы должны преобразовать 1 в 0. Для этого мы вычитаем строку 1 из строки 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 1 & 2 & 2 & 0 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 - f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-83933b5a2315a4dcbc770bf92bf3831b_l3.png)
Переходим ко второму столбцу: сначала преобразуем 4 в 1, разделив вторую строку на 4:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 4 & 2 & -1 & 1 & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2/4} \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-298984c72a249e2b5c98740cc0c1a11e_l3.png)
Единичная матрица имеет 0 в первом элементе второго столбца, где теперь стоит -2. Поэтому мы должны преобразовать -2 в 0. Для этого мы добавляем строку 2, умноженную на 2, к строке 1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & -2 & 0 & 1 & 0 & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1\end{array} \right) \begin{array}{c} \xrightarrow{f_1 +2f_2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3dfcdcb586eed87861b3ac0ea46bea2f_l3.png)
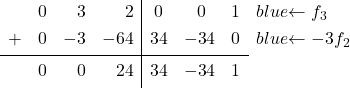
Единичная матрица имеет 0 в последнем элементе второго столбца, где теперь есть 3. Поэтому мы должны преобразовать 3 в 0. Для этого из строки 3 мы вычитаем строку 2, умноженную на 3:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 3 & 2 & 0 & 0 & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3 -3f_2} \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-94ed5a1b9cf1db0bfb99ce79d0a6d36b_l3.png)
Переходим к третьему столбцу: мы должны преобразовать последний
![]()
в 1. Для этого умножаем третью строку на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 &\sfrac{2}{4} & \sfrac{3}{4} & \sfrac{-3}{4} & 1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{2f_3 } \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-a8134938726d3b48fe3d7d789260b128_l3.png)
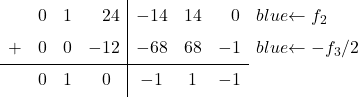
Единичная матрица имеет 0 во втором элементе последнего столбца. Поэтому необходимо преобразовать
![]()
в 0. Для этого из строки 2 вычитаем строку 3, разделенную на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & \sfrac{2}{4} & \sfrac{-1}{4} & \sfrac{1}{4} & 0 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2-f_3/2 } \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b91b71183a50e41e9be5c7305f8cf3e_l3.png)
Все, что нам нужно сделать сейчас, это преобразовать первый элемент третьего столбца в 0. Для этого вычтем строку 3 из строки 1:

![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|ccc}1 & 0 & 1 & \sfrac{2}{4} & \sfrac{2}{4} & 0 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right) \begin{array}{c} \xrightarrow{f_1-f_3 } \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|ccc} 1 & 0 & 0 & -1 & 2 & -2 \\[2ex] 0 & 1 & 0 & -1 & 1 & -1 \\[2ex] 0 & 0 & 1 & \sfrac{6}{4} & \sfrac{-6}{4} & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2023374b9885dd33fe4d3c12e5a4de59_l3.png)
Таким образом, обратная матрица равна:
![Rendered by QuickLaTeX.com A^{-1}= \left( \begin{array}{ccc} -1 & 2 & -2 \\[2ex] -1 & 1 & -1 \\[2ex] \sfrac{6}{4} &\sfrac{-6}{4} & 2 \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0854e7cb80ba561b6e0c724a9a9b5fff_l3.png)
Наконец, дроби обратной матрицы можно упростить:
![Rendered by QuickLaTeX.com \bm{A^{-1}= \left( } \begin{array}{ccc} \bm{-1} & \bm{2} & \bm{-2} \\[2ex] \bm{-1} & \bm{1} & \bm{-1} \\[2ex] \sfrac{\bm{3}}{\bm{2}} &\sfrac{\bm{-3}}{\bm{2}} & \bm{2} \end{array} \bm{ \right)}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c7ef6b6cdca2f4a808ed9457bde3b3f_l3.png)
Свойства обратной матрицы
Обратная матрица имеет следующие характеристики:
- Обратная матрица уникальна .
- Инверсией обратной матрицы является исходная матрица:
![]()
- Обратное произведение двух матриц равно произведению обратных матриц, но с изменением их порядка.
![]()
- Транспонировать матрицу , а затем выполнить обратную матрицу, это все равно, что сначала выполнить инверсию матрицы, а затем ее транспонировать.
![]()
- Чтобы найти определитель обратной матрицы, мы можем вычислить определитель матрицы, а затем выполнить его обратную операцию, поскольку обе операции дают один и тот же результат.
![]()
Формула для быстрого расчета обратной матрицы 2×2
Как мы видели, любую матрицу можно обратить методом определителей или методом Гаусса. Но отдельно есть еще формула, позволяющая очень быстро найти обратную матрицу 2×2 :
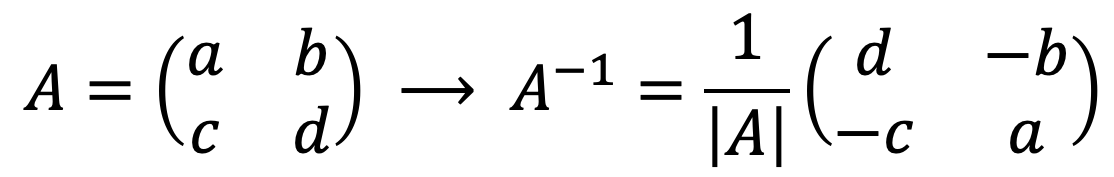
Как видите, инвертировать матрицу 2х2 просто: достаточно решить определитель матрицы
![]()
, чередовать положение элементов главной диагонали и менять знак элементов второстепенной диагонали.
Пример того, как получить обратную матрицу 2×2 по формуле
Вычислите обратную следующую квадратную матрицу 2 × 2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-599baee27c05b5610a8714363e1260eb_l3.png)
Определитель матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{vmatrix} & = 3 \cdot (-4)- (-2) \cdot 5 \\ & = -12-(-10) \\[2ex] & =-12+10\\[2ex] &=-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ab99f7b87d01c670a8598df6364ab58f_l3.png)
Теперь применим формулу обратной матрицы :
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{-2} \begin{pmatrix} -4 & -5 \\[1.1ex] 2 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-68fd6e830b576af8abf55be1e11fbafb_l3.png)
И умножаем матрицу на дробь:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} =\begin{pmatrix} \cfrac{-4}{-2} & \cfrac{-5}{-2} \\[3ex] \cfrac{2}{-2} & \cfrac{3}{-2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-41da8ef6bef1d339337717ed4ad86ae5_l3.png)
Таким образом, инвертированная матрица A равна:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{2} & \cfrac{\bm{5}}{\bm{2}} \\[3ex] \bm{-1} & \bm{-}\cfrac{\bm{3}}{\bm{2}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29da2a64f6da927857de112ca8363ba5_l3.png)
Как видите, инвертировать матрицу по этой формуле гораздо быстрее, но использовать ее можно только с матрицами размерности 2×2.
Решенные упражнения на обратные матрицы 2×2 по формуле
Упражнение 1
Инвертируйте следующую матрицу размером 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc06e21fc1c3c54f9b3fc0dcd4912a8f_l3.png)
Определитель матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{vmatrix} & = 2 \cdot 3- 1 \cdot 5 \\ & = 6-5 \\[2ex] & =1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b0ae510ea7a336cbe5ea56a554da719_l3.png)
Теперь применим формулу для нахождения обратной матрицы:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 5 \\[1.1ex] 1 & 3 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{1} \begin{pmatrix} 3 & -5 \\[1.1ex] -1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8f18178c829fd38360a04a947d52017_l3.png)
Таким образом, обратная матрица A равна:
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{3} & \bm{-5} \\[1.1ex] \bm{-1} & \bm{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-237fe82cd91972f667f6751fa4735534_l3.png)
Упражнение 2
Вычислите обратную матрицу второго порядка:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f2289d1c5c9aeb87016f719305d900a7_l3.png)
Определитель матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{vmatrix} & = 2 \cdot (-2)- (-1) \cdot 6 \\ & = -4-(-6) \\[2ex] & =-4+6 \\[2ex] & =2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fef2cc00702131123994cc588bf7ea_l3.png)
Теперь применим формулу для решения обратной матрицы размерности 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 2 & 6 \\[1.1ex] -1 & -2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{2} \begin{pmatrix} -2 & -6 \\[1.1ex] 1 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2de7166a0cf59e0f8c5b7750e1947f04_l3.png)
И, наконец, делаем умножение:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{-2}{2} & \cfrac{-6}{2} \\[3ex] \cfrac{1}{2} & \cfrac{2}{2} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f6a5973078468914beb4bd4d85a40331_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-1} & \bm{-3} \\[2ex] \cfrac{\bm{1}}{\bm{2}} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a540a077ee9a24da96fa988410aef429_l3.png)
Упражнение 3
Инвертируйте следующую матрицу 2×2:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36e230a808c42411a9cfd2d9eb44543d_l3.png)
Определитель матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} 4 & 1 \\[1.1ex] 5 & 2\end{vmatrix} & = 4 \cdot 2 - 5 \cdot 1 \\ & = 8-5 \\[2ex] & =3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e7a6c5ef316ae51b43c90863c6245780_l3.png)
Теперь применим формулу для расчета обратной матрицы размерности 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{3} \begin{pmatrix} 2 & -1 \\[1.1ex] -5 & 4 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e2f359bd166c295b869a8cf04d927097_l3.png)
И, наконец, делаем произведение дроби на матрицу:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{\bm{2}}{\bm{3}} & \bm{-}\cfrac{\bm{1}}{\bm{3}} \\[3ex] \bm{-}\cfrac{\bm{5}}{\bm{3}} & \cfrac{\bm{4}}{\bm{3}} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a02ea2e547dcc21081ae80df407a4e0_l3.png)
Упражнение 4
Найдите обратную матрицу второго порядка:
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-422fcd6f391a2682e4b546c9e9c05b55_l3.png)
Определитель матрицы A:
![Rendered by QuickLaTeX.com \displaystyle \begin{aligned}\begin{vmatrix}A\end{vmatrix} = \begin{vmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{vmatrix} & = (-2) \cdot 10- (-3) \cdot 5 \\ & = -20-(-15) \\[2ex] & =-20+15 \\[2ex] & =-5\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e9997751e16d3b976454be828cb914d_l3.png)
Теперь применим формулу для создания обратной матрицы размером 2×2:
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}\longrightarrow A^{-1} = \cfrac{1}{|A|} \begin{pmatrix} d & -b \\[1.1ex] -c & a \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d5308484309da4485a3d9b92af86e7d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} -2 & 5 \\[1.1ex] -3 & 10\end{pmatrix} \longrightarrow A^{-1} = \cfrac{1}{-5} \begin{pmatrix} 10 & -5 \\[1.1ex] 3 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c0c614039614bd9125b2920da8698eb_l3.png)
И, наконец, делаем умножение:
![Rendered by QuickLaTeX.com \displaystyle A^{-1} = \begin{pmatrix} \cfrac{10}{-5} & \cfrac{-5}{-5} \\[3ex] \cfrac{3}{-5} & \cfrac{-2}{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-edb1dfc870b3045eaefc1716a80e2ca2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \bm{A^{-1} =}\begin{pmatrix} \bm{-2} & \bm{1} \\[2ex] \bm{-}\cfrac{\bm{3}}{\bm{5}} & \cfrac{\bm{2}}{\bm{5}} \ \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5c49e161c701254cfbe20353c11980eb_l3.png)
Решите систему уравнений с обратной матрицей
Трудно оценить реальное применение обратной матрицы. На самом деле, вам, наверное, интересно… для чего используется обратная матрица? Действительно ли он для чего-нибудь используется?
Ну и одно из применений обратной матрицы — решение систем линейных уравнений . И да, хотя может показаться, что это две совершенно разные концепции, можно найти решение системы уравнений, обратив матрицу.
Давайте посмотрим на примере, как это делается:
- Вычислите решение следующей системы уравнений с обратной матрицей:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+3y=5 \\[2ex] 2x+4y=6 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-200c0f994f86752e7d650621a0d4100f_l3.png)
Прежде всего, необходимо заметить, что систему уравнений можно выразить в виде матриц:
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\begin{pmatrix} x \\[1.1ex]y \end{pmatrix} = \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b9c9f181fc16a501799145c516a9747_l3.png)
Мы можем убедиться, что эта матричная форма системы эквивалентна выражению с уравнениями: если мы перемножим матрицы, то увидим, что получаем два уравнения системы.
Теперь, чтобы упростить следующие шаги, мы вызовем
![]()
к матрице, содержащей коэффициенты при неизвестных,
![]()
к столбцам матрицы с неизвестными, и
![]()
к матрице-столбцу с независимыми членами:
![]()
Итак, матрица
![]()
– неизвестное матричного уравнения.
Чтобы решить это матричное уравнение, вы должны выполнить процедуру, которую мы не будем здесь объяснять столь подробно. Если вы хотите понять это полностью, вы можете узнать, как решать уравнения с матрицами , где мы шаг за шагом объясняем весь процесс.
Эта процедура основана на свойстве обратных матриц: любая матрица, умноженная на обратную, равна единичной (или единичной) матрице. Следовательно, неизвестная матрица легко решается
![]()
умножив обе части уравнения на обратную матрицу A:
![]()
![]()
![]()
![]()
И как только мы изолировали матрицу
![]()
, мы вычисляем обратную величину
![]()
и решаем произведение матриц:
![Rendered by QuickLaTeX.com \displaystyle X=\left.\begin{pmatrix} 1 & 3 \\[1.1ex] 2 & 4 \end{pmatrix}\right.^{-1}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a1290e37a9e3f56fc6b288bc7686d66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X=\cfrac{1}{-2} \begin{pmatrix} 4 & -3 \\[1.1ex] -2 & 1 \end{pmatrix}\cdot \begin{pmatrix} 5 \\[1.1ex] 6 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-21471fc8a4c04aac3121519e8ef874e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle X= \begin{pmatrix} -1 \\[1.1ex] 2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b9457fedf68c4bdfea898922e465eeb8_l3.png)
Таким образом, решение системы уравнений имеет вид:
![]()