▷ Как разрешить все виды неопределенностей (пределов)

В этой статье мы объясним, что такое неопределенность. Вы узнаете, что представляют собой все типы неопределенностей и как их разрешить. Кроме того, вы сможете увидеть пошагово решенные упражнения на пределы функций всех неопределенностей.

Что такое неопределенности?

Неопределенности, также называемые неопределенными формами, представляют собой математические выражения, которые появляются при вычислении пределов функций, результат которых не определен. Таким образом, для разрешения неопределенностей пределов необходимо применить предварительную процедуру, которая зависит от типа функции.

То есть, когда мы получаем неопределенность, это не означает, что предела не существует или что он не может быть решен, а скорее то, что нам придется внести изменения в функцию, чтобы найти решение предела.

Виды неопределенностей

Неопределенности, или неопределенные формы, подразделяются на следующие виды:

Неопределенность бесконечность минус бесконечность (∞-∞)
Число неопределенностей между нулем (k/∞)
Нулевая неопределенность между нулем (0/0)
Бесконечная неопределенность между бесконечностью (∞/∞)
Неопределенность 1 возведена в бесконечность (1 ^∞ )
Нулевая неопределенность повышена до нуля (0 ⁰ )
Нулевая неопределенность для бесконечности (0·∞)
Нулевая неопределенность, возведенная до бесконечности (0 ^∞ )
Бесконечная неопределенность, доведенная до нуля (∞ ⁰ )

Затем мы увидим, как разрешить все типы неопределенностей.

Бесконечность минус бесконечная неопределенность

Неопределенная форма бесконечность минус бесконечность не равна нулю, так как мы вычитаем два очень больших числа, но не знаем, какое из них больше. Следовательно, результат разности бесконечностей зависит от порядка каждой бесконечности.

$\infty-\infty$

Разрешить неопределенность такого типа непросто, поскольку в зависимости от типа функции необходимо применять ту или иную процедуру. Поэтому мы рекомендуем вам просмотреть полное объяснение по следующей ссылке:

➤ См.: как решить неопределенность бесконечность минус бесконечность

Число неопределенностей между нулем

Неопределенность константы, деленной на ноль, получается при сокращении знаменателя рациональной функции.

$\cfrac{k}{0}$

Результат этого типа неопределенной формы всегда будет более бесконечным, менее бесконечным или предел функции не будет существовать. Давайте посмотрим, как вычисляется эта неопределенность, решая предел на примере:

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

Мы получили неопределенность числа, разделенного на ноль, поэтому нам необходимо вычислить боковые пределы функции:

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ Смотрите: что такое боковые пределы?

Два боковых предела функции дают один и тот же результат, поэтому по определению предел функции, когда x стремится к 0, дает минус бесконечность:

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

Обратите внимание: если бы боковые пределы давали разные значения, предела функции в этой точке не существовало бы.

Ноль между нулевой неопределенностью

Неопределенный предел нуля, разделенный на ноль, очень распространен и получается в функциях с дробями, в которых числитель и знаменатель сокращаются.

$\cfrac{0}{0}$

Этот тип неопределенного предела разрешается по-разному в зависимости от функции. Например, если функция имеет корни, необходимо выполнить разные шаги. Вы можете увидеть различные разрешения этого типа неопределенности по следующей ссылке:

➤ См.: как решить нулевую неопределенность между нулем

Бесконечная неопределенность между бесконечным

Бесконечная неопределенность между бесконечностью обычно возникает в бесконечных пределах функций с дробями. Хотя неопределенность — это частное двух бесконечностей, результат не обязательно должен быть бесконечностью.

$\cfrac{\infty}{\infty}$

Этот тип неопределенной формы разрешается путем сравнения. То есть соблюдается степень числителя и степень знаменателя и в зависимости от того, какая из них больше, предельный результат получается тот или иной. Посмотреть все случаи можно по следующей ссылке:

➤ См.: решенные упражнения на бесконечные пределы между бесконечностью

Неопределенность 1 возведена в бесконечность

С математической точки зрения можно было бы подумать, что от 1 до бесконечности получается 1, поскольку любая степень 1 равна 1. Однако этот член является неопределенностью, и, следовательно, невозможно так же легко вывести его результат.

$1^{\infty}$

Этот тип неопределенности рассчитывается по следующей формуле:

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

Например, следующий предел является неопределенным, поскольку он дает степень бесконечности:

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

Поэтому мы должны использовать формулу для этого типа неопределенности:

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

Итак, мы уже разрешили неопределенный предел, возведенный в бесконечность.

Нулевая неопределенность сведена к нулю

Нулевая неопределенность в нулевой степени возникает в пределах сложных функций.

$0^0$

Чтобы разрешить этот тип неопределенного лимита, необходимо использовать следующее свойство лимита:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Например, следующий предел дает неопределенную форму 0 в степени 0:

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

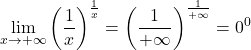
Но если применить к пределу логарифмы, мы сможем найти его значение:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

Нулевая неопределенность для бесконечности

Трудно столкнуться с неопределенностью произведения нуля и бесконечности , но это не значит, что его легко определить.

$0\cdot \infty$

Единого метода разрешения неопределенности этого типа не существует, но он зависит от типа функции. В этом случае мы должны преобразовать функцию в бесконечную неопределенность, деленную на бесконечность, или в нулевую неопределенность, разделенную на ноль, и оттуда применить методы решения, которые мы видели выше для каждой неопределенности.

Итак, если предел одной функции равен 0, а предел другой функции равен ∞:

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

Мы можем трансформировать этот тип бесконечно, внеся следующие изменения:

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

Давайте посмотрим, как это сделать, на примере решения неопределенного предела:

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

Мы воздействуем на функцию, чтобы получить бесконечную неопределенность на бесконечности, затем находим предел:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

Нулевая неопределенность возведена в бесконечность

Ноль неопределенности, возведенный до бесконечности, немного сложно понять, поскольку мы возводим очень маленькое число в очень большое.

$0^{\infty}$

При получении этих неопределенных форм необходимо использовать следующую формулу:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Давайте решим пример, чтобы лучше понять, как вычислить этот тип неопределенности:

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

Бесконечная неопределенность сведена к нулю

Обычно любая степень, возведенная в ноль, дает 1, однако неопределенность бесконечности, возведенная в ноль , не обязательно должна быть такой.

$\infty^0$

Как и в случае с неопределенностями, возведенными в ноль и нулем, возведенными в бесконечность, для решения этого типа неопределенного предела необходимо применить логарифмы:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Давайте посмотрим, как решается этот тип неопределенных пределов, пошагово рассчитав пример:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

Виды неопределенностей (неопределенных пределов)

Что такое неопределенности?

Виды неопределенностей

Бесконечность минус бесконечная неопределенность

Число неопределенностей между нулем

Ноль между нулевой неопределенностью

Бесконечная неопределенность между бесконечным

Неопределенность 1 возведена в бесконечность

Нулевая неопределенность сведена к нулю

Нулевая неопределенность для бесконечности

Нулевая неопределенность возведена в бесконечность

Бесконечная неопределенность сведена к нулю

Оставьте комментарий Отменить ответ