На этой странице мы объясняем, что такое линейно независимые и линейно зависимые векторы. Вы также увидите примеры того, как определить, является ли набор векторов линейно зависимым или независимым. А, кроме того, вы найдете пошаговые упражнения и решаемые задачи на линейную независимость и зависимость.
Что такое линейно независимые векторы?
Множество свободных векторов называется линейно независимым, если ни один из них не может быть записан в виде линейной комбинации других.
Другими словами, для данного набора векторов
![]()
Они линейно независимы, если единственное решение следующего уравнения:
![]()
Это все коэффициенты
![]()
равно 0:
![]()
Геометрически два вектора линейно независимы, если они не имеют одного и того же направления, то есть если они не параллельны.
Для краткости иногда прямо говорим, что это векторы LI. Или что векторы обладают линейной независимостью.
Что такое линейно зависимые векторы?
Очевидно, что линейно зависимые векторы означают противоположность линейно независимым векторам. Поэтому его определение таково:
Множество свободных векторов плоскости линейно зависимо, если любой из них можно выразить как линейную комбинацию других векторов, образующих систему.
Другими словами, для данного набора векторов
![]()
Они линейно зависимы, если существует решение следующего уравнения:
![]()
в котором имеет определенный коэффициент
![]()
отличается от 0:
![]()
Верно и обратное: если вектор представляет собой линейную комбинацию других векторов, то все векторы в наборе линейно зависимы.
Кроме того, если два вектора параллельны, это означает, что они линейно зависимы.
Иногда их также сокращают и называют просто векторами LD. Или даже что векторы имеют линейную зависимость.
Пример того, как узнать, являются ли векторы линейно зависимыми или независимыми
Затем мы увидим типичный пример линейно зависимых и независимых векторов.
- Определите, имеют ли следующие 3 трехмерных вектора линейную зависимость или независимость:
![]()
![]()
![]()
Во-первых, нам нужно сформулировать условие линейной комбинации:
![]()
Теперь заменим каждый вектор его координатами. Как ноль, который соответствует нулевому вектору:
![]()
Коэффициенты умножают векторы, поэтому следующее выражение эквивалентно:
![]()
Добавляем векторы:
![]()
Если присмотреться, то предыдущему выражению соответствуют 3 уравнения, так как каждая координата левого вектора должна быть равна каждой координате правого вектора. Таким образом, мы имеем однородную систему из трех уравнений с тремя неизвестными:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c6bb8117dd8ae715314efe73fe65eed8_l3.png)
Поэтому единственное, что нам нужно сделать, это решить систему уравнений, неизвестные которой равны
![]()
И
![]()
Для этого можно использовать любой метод (метод замены, метод Гауса, правило Крамера и т. д.). Однако, чтобы узнать, являются ли векторы LI или LD, достаточно определить, существует ли решение, отличное от тривиального решения (все коэффициенты равны нулю). ТАК:
- Если определитель матрицы, составленной из компонент векторов, отличен от нуля, это означает, что система уравнений имеет только одно решение (
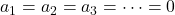
) и, следовательно, векторы линейно независимы
- С другой стороны, если определитель матрицы, составленной из компонент векторов, равен нулю, это означает, что система уравнений имеет более одного решения и, следовательно, векторы линейно зависимы .
Таким образом, единственное, что необходимо вычислить, — это определитель с координатами векторов (поскольку это определитель 3×3, его можно решить с помощью правила Сарруса). Этот определитель соответствует коэффициентам предыдущей системы уравнений:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-046e05ff603822985510c7bdc8b73021_l3.png)
В этом случае определитель отличен от 0, поэтому векторы линейно независимы .
Поэтому единственным возможным решением системы уравнений является тривиальное решение со всеми неизвестными, равными нулю:
![]()
Свойства линейно зависимых и независимых векторов
Линейная зависимость или независимость векторов имеет следующие характеристики:
- Два пропорциональных вектора параллельны и, следовательно, линейно зависимы, поскольку имеют одинаковое направление.
- Аналогично, если два вектора не имеют одинакового направления или непропорциональны, они линейно независимы.
- Три компланарных вектора (находящиеся в одной плоскости) линейно независимы.
- Нулевой вектор
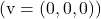
линейно зависит от любого вектора.
- Набор линейно независимых векторов порождает векторное пространство и образует векторный базис. Если три вектора перпендикулярны, это ортогональная база. А если его модуль также равен 1, это соответствует ортонормированному базису.
Решенные упражнения на линейную зависимость и независимость
Ниже вы можете попрактиковаться в нескольких решенных упражнениях с линейно зависимыми и независимыми векторами.
Упражнение 1
Определите, являются ли следующие векторы линейно зависимыми или независимыми:
![]()
![]()
![]()
Сначала сформулируем условие линейной комбинации:
![]()
![]()
![]()
![]()
Предыдущему равенству соответствует следующая система линейных уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-58f1b449f48096570437df0ca40f8a8d_l3.png)
После того, как мы сформулировали систему уравнений, мы решаем определитель матрицы с ее членами:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-caa6d4f135e79bb8b6d2368ff7eebefb_l3.png)
В этом случае определитель отличен от 0, поэтому три вектора линейно независимы друг от друга.
Упражнение 2
Классифицируйте следующие векторы как линейно зависимые или независимые:
![]()
![]()
![]()
Прежде всего сформулируем уравнение линейной комбинации:
![]()
![]()
![]()
![]()
Из предыдущего равенства получаем следующую однородную систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c94610b6f8baef34a1fb4601c148f515_l3.png)
После того, как мы сформулировали систему уравнений, находим определитель матрицы с координатами векторов:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67678c37fdaf0955ef8bbab8d34379f8_l3.png)
В этом случае определитель эквивалентен 0, поэтому три вектора зависят друг от друга линейно .
Упражнение 3
Для следующих трех векторов укажите, какие пары векторов линейно зависимы, а какие пары линейно независимы.
![]()
Самый простой способ определить, является ли пара векторов линейно зависимой или независимой, — это проверить, пропорциональны ли они.
Сначала проверяем вектор
![]()
с вектором
![]()
![]()
Во-вторых, мы проверяем вектор
![]()
с вектором
![]()
![]()
Наконец, мы проверяем вектор
![]()
с вектором
![]()
![]()
Таким образом, единственной парой векторов, которая линейно зависит друг от друга, является
![]()
И
![]()
Более того, их взаимоотношения таковы:
![]()
Или эквивалент:
![]()
С другой стороны, остальные пары векторов линейно независимы.
Упражнение 4
Изучите линейную зависимость или независимость следующих 4-х векторов друг от друга:
![]()
![]()
![]()
![]()
Сначала сформулируем условие линейной комбинации:
![]()
![]()
![]()
![]()
В данном случае мы имеем систему трех уравнений с четырьмя неизвестными:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e9451263e5a31994569292e32666d93e_l3.png)
Мы не можем решить определитель всей матрицы системы, так как можно определить только квадратные матрицы. Поэтому мы должны вычислить все возможные комбинации определителей 3×3 и посмотреть, равен ли один из них 0, и в этом случае векторы будут линейно зависимы, с другой стороны, если все определители отличны от 0, 4 вектора будут быть линейно независимым.
Вычисляем определитель коэффициентов
![]()
И
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&4\\[1.1ex] 1&-2&1 \\[1.1ex] 2&0&-1 \end{vmatrix} =13\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-488d7848a40aa9a91bd5b3aa1f09b774_l3.png)
Определитель первых трёх коэффициентов (или первых трёх векторов) отличен от нуля. Итак, теперь мы попробуем с определителем коэффициентов
![]()
И
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 0&-1&-2\\[1.1ex] 1&-2&-3 \\[1.1ex] 2&0&2 \end{vmatrix} \bm{= 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1475a77f10ea0c16147a6f9c3f611b4_l3.png)
Мы получили нулевой определитель, поэтому нет необходимости вычислять остальные определители, поскольку мы уже знаем, что 4 вектора линейно зависимы .
Упражнение 5
Рассчитайте стоимость
![]()
так что следующие векторы линейно независимы:
![]()
![]()
![]()
Прежде всего сформулируем уравнение линейной комбинации:
![]()
![]()
![]()
![]()
Из предыдущего векторного уравнения получаем следующую однородную систему уравнений:
![Rendered by QuickLaTeX.com \left. \begin{array}{l}3a_1-2a_2+a_3= 0 \\[2ex] -a_1+4a_2+3a_3 =0\\[2ex] 5a_1+7a_2+ka_3 = 0 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-16f88cbf406c1faf61307b99179a5de6_l3.png)
После того как мы сформулировали систему уравнений, попробуем решить определитель системы:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 3&-2&1\\[1.1ex] -1&4&3 \\[1.1ex] 5&7&k \end{vmatrix} =10k-120](https://mathority.org/wp-content/ql-cache/quicklatex.com-d748080bb1cacc1c80a35ef633a2d85e_l3.png)
Утверждение говорит нам, что векторы должны быть линейно зависимыми. Поэтому определитель должен быть равен нулю:
![]()
![]()
![]()
![]()
Поэтому константа должна быть равна 12, чтобы векторы имели линейную зависимость.