Мономы — маторность

Здесь мы объясняем все, что вам нужно знать об мономах: что они собой представляют, из каких частей состоят (и как их идентифицировать), различные типы мономов, как вычислять операции с мономами, числовое значение монома. .. Кроме того, вы сможете увидеть примеры и упражнения, решаемые пошагово одночленов.

Что такое мономы?

В математике определение монома следующее:

Моном – это алгебраическое выражение, образованное комбинацией цифр и букв. Точнее, моном состоит из произведения числа и одной или нескольких переменных (букв), возведенных в степень.

Например, член 7x ³ y ² называется мономом, потому что он имеет число (7) и разные буквы (x, y).

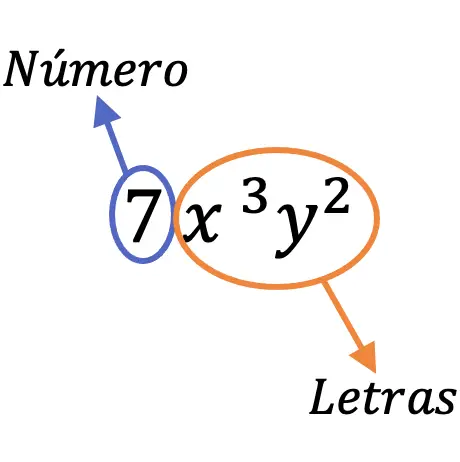
Части монома

Теперь, когда мы поняли значение монома, давайте посмотрим, каковы все части монома:

Коэффициент : число, на которое умножаются переменные (или буквы) монома.
Переменная : каждая буква, входящая в моном.
Буквальная часть : соответствует всем переменным, составляющим моном, со всеми соответствующими показателями.
Степень : состоит из суммы всех показателей букв, образующих моном.

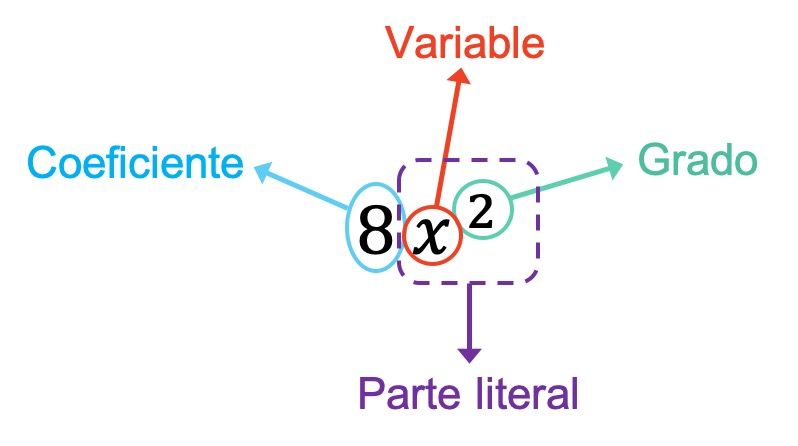
Коэффициент монома в приведенном выше примере равен 8, поскольку это число, на которое умножаются переменные. Кроме того, в этом случае моном имеет только одну переменную — x. Итак, буквальная часть монома образована этой переменной плюс ее показатель степени, равный x ² . Наконец, степень монома равна 2, потому что это единственная степень, которую он имеет.

Теперь попробуйте решить следующее упражнение на части одночлена:

Определите все части следующего монома:

$5x^4y^2z$

посмотреть решение

Компонентами монома высказывания являются:

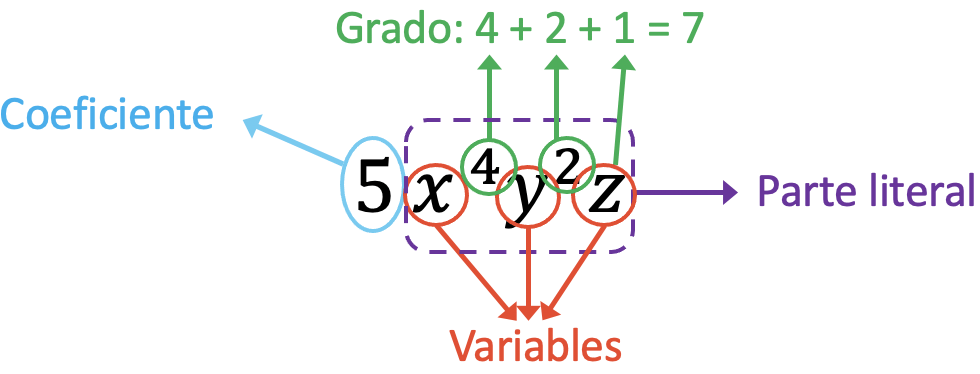
упражнения решаются шаг за шагом одночленов

Коэффициент при мономе в задаче равен 5, так как именно на этот член умножаются буквы. С другой стороны, переменными этого монома являются x, y, z. В-третьих, буквенная часть монома соответствует выражению x ⁴ y ² z. И наконец, степень монома равна сумме всех показателей переменных, т.е. 7 (4+2+1=7).

Обратите внимание: если у буквы нет показателя степени, это фактически означает, что ее показатель степени равен 1. Поэтому, чтобы вычислить степень монома задачи, мы добавляем единицу, которая представляет показатель степени переменной z.

Виды одночленов

Существуют разные типы мономов, каждый из которых обладает своими свойствами. Наиболее важными мономами являются подобные мономы, однородные мономы, гетерогенные мономы и противоположные мономы. Далее мы увидим характеристики каждого типа.

подобные мономы

Подобные мономы – это мономы, имеющие одинаковую буквальную часть. Следовательно, два или более одночленов подобны, если они имеют одинаковые буквы и показатели степени.

Например, следующие два монома похожи, потому что, хотя они и имеют разные коэффициенты, они образованы одними и теми же переменными и возведены в одни и те же показатели степени.

$4x^5y^3 \qquad \qquad 9x^5y^3$

Как мы увидим позже, этот тип мономов используется для решения операций над мономами.

однородные мономы

Два монома однородны, если их абсолютная степень равна.

Например, следующие два монома однородны, поскольку степень обоих равна 5:

$2x^5 \qquad \qquad 6x^2y^3$

У первого монома есть единственная переменная, возведенная в степень 5, поэтому его степень равна 5. А у второго многочлена одна переменная возведена в квадрат, а другая — в куб, поэтому его степень также равна 5 (2+3 =5).

Как видим, для того чтобы два монома были однородными, им не обязательно иметь одинаковую буквальную часть, а достаточно иметь одинаковую абсолютную степень.

гетерогенные мономы

Гетерогенные мономы – это мономы, не имеющие одинаковой абсолютной степени. Другими словами, гетерогенные мономы являются противоположностью однородных мономов.

Следующие три монома неоднородны, поскольку каждый из них имеет разную степень:

$x^8 \qquad 3xy \qquad 7a^9b^2$

Первый моном имеет степень 8, второй моном — степени 2, а третий моном — степени 11. Следовательно, эти три монома неоднородны друг другу.

Противоположные мономы

Противоположные мономы — это мономы, которые однородны (имеют одинаковую буквенную часть) и при этом их коэффициенты противоположны, т. е. их коэффициенты имеют одинаковое значение, но противоположный знак.

Например, следующие два монома являются противоположностями:

$3x^5y^2 \qquad \qquad -3x^5y^2$

Два предыдущих монома являются противоположными, потому что они различаются только знаком: первый имеет положительный знак, а второй отрицательный.

Теперь, когда вы увидели несколько примеров мономов, вас может заинтересовать другое похожее алгебраическое выражение: бином . На самом деле бином состоит из сложения (или вычитания) нескольких мономов, поэтому интересно посмотреть на связь между этими двумя понятиями. Вы можете увидеть, что означает бином, нажав на эту ссылку.

Действия с одночленами

Чтобы углубить понятие мономов, мы посмотрим, какие операции можно производить с мономами. В частности, мономы можно складывать, вычитать, умножать, делить и возводить в степень. И каждый вид операции имеет свои особенности, поэтому ниже мы разберем их по отдельности.

сумма одночленов

Два или более одночленов можно складывать только в том случае, если они являются одинаковыми одночленами. Тогда сумма двух подобных одночленов равна другому одночлену, составленному из той же буквенной части и суммы коэффициентов этих двух одночленов.

Примеры сумм мономов

$2x^4+3x^4 = 5x^4$
$4y^2+y^2 = 5y^2$
$7x^3y+2x^3y = 9x^3y$
$2a^3b^2c^6+6a^3b^2c^6 = 8a^3b^2c^6$
$4x^3+2x^3+5x^3=6x^3+5x^3=11x^3$

Если вы хотите попрактиковаться в выполнении упражнений на сложение одночленов, вы можете поискать их в поисковой системе справа вверху, потому что у нас есть целая страница, полная решенных упражнений на сложение одночленов.

вычитание одночленов

Два или более монома можно вычесть только в том случае, если они подобны. Таким образом, вычитание двух подобных одночленов равно другому одночлену, составленному из той же буквенной части, и вычитанию коэффициентов этих двух одночленов.

Примеры вычитания мономов

$7x^2-4x^2 = 3x^2$
$5y^3-y^3 = 4y^3$
$8x^6y-4x^6y = 4x^6y$
$10a^3b^4c^2-6a^3b^4c^2 = 4a^3b^4c^2$
$11x^3-4x^3-5x^3=7x^3-5x^3=2x^3$

Вы можете попрактиковаться с решенными пошаговыми упражнениями на вычитание одночлена , которые можно найти на нашем сайте. Найти их можно через поисковик вверху справа.

умножение одночленов

Результатом умножения двух мономов является другой моном, коэффициент которого является произведением коэффициентов мономов и буквенная часть которого получается умножением переменных, имеющих одинаковую основу, то есть сложением их экспонентов.

Итак, чтобы найти произведение двух разных мономов, необходимо перемножить коэффициенты и сложить показатели степеней, имеющих одинаковое основание.

С другой стороны, если мы умножим два монома с разной базовой степенью, нам просто придется умножить их коэффициенты вместе, а степени оставить прежними:

$5x^2\cdot 3y^4 = (5\cdot 3) x^2y^4 = 15x^2y^4$

Примеры умножения одночленов

$6x^4 \cdot 7x^5= (6\cdot 7)x^{4+5} = 42x^9$
$4y \cdot 2y^3 = (4\cdot 2)y^{1+3} = 8 y^4$
$5x^2y^4\cdot (-8x^8y^2)=(5\cdot (-8))x^{2+8}y^{4+2} = -40x^{10}y^6$
$-3x^6y^4 \cdot (-4x^2z)= (-3\cdot (-4)) x^{6+2}y^4z= 12x^8y^4z$
$-3x^8\cdot 4x^5\cdot (-x^2) =-12x^{13}\cdot (-x^2)= 12x^{15}$

Чтобы попрактиковаться в решении пошаговых упражнений на умножение одночленов, вы можете обратиться к статье, которая есть на этом сайте. Вы легко найдете его с помощью поисковой системы в правом верхнем углу.

деление одночленов

Результатом деления мономов является другой моном, коэффициент которого эквивалентен частному коэффициентов мономов и буквенная часть которого получается делением переменных, имеющих одинаковое основание, то есть вычитанием их экспонентов.

Итак, чтобы разделить два разных монома, мы просто разделяем коэффициенты между ними и вычитаем показатели степеней, имеющих одинаковое основание.

Примеры деления одночленов

$7x^6 : 7x^4= (7:7)x^{6-4} = 1x^2=x^2$
$12y^5 : 4y^2= (12:4)y^{5-2} = 3y^3$
$15x^7y^6 :3x^4y^5= (15:3)x^{7-4}y^{6-5} = 5x^3y$
$27x^9y^7 :(-3x^5y^2)= (27:(-3))x^{9-5}y^{7-2}= -9x^4y^5$
$-18x^{13} : 3x^4 : (-2x^7) = -6x^9: (-2x^7) = 3x^2$

Деление одночленов сложнее, чем кажется, поэтому мы рекомендуем вам попробовать пошагово выполнить имеющиеся у нас решенные упражнения по делению одночленов . Самый быстрый способ найти их — через нашу поисковую систему в правом верхнем углу.

степень монома

Чтобы вычислить степень монома, каждый элемент монома необходимо возвести в показатель степени . Другими словами, степень монома состоит из возведения его коэффициента и его переменных (букв) в показатель степени.

Из свойств степеней помните, что когда мы возводим уже возведенный член, два показателя степени перемножаются. По этой причине в степени монома показатель степени каждой буквы всегда умножается на показатель, обозначающий степень .

Примеры степеней одночленов

$\left(5x^6\right)^2 = 5^2\left(x^6\right)^2 = 5^2x^{6\cdot 2} = 25x^{12}$
$\left(2x^5\right)^4 = 2^4\left(x^5\right)^4 = 2^4x^{5\cdot 4} = 16x^{20}$
$\left(-4y^3\right)^2 = (-4)^2\left(y^3\right)^2 = (-4)^2y^{3\cdot 2} = 16y^{6}$
$\left(3x^4y\right)^3 = 3^3\left(x^4y\right)^3 = 3^3x^{4\cdot 3}y^{1\cdot 3} = 27x^{12}y^3$
$\left(-2a^5b^7\right)^3 = (-2)^3\left(a^5b^7\right)^3 = (-2)^3a^{5\cdot 3}b^{7\cdot 3} = -8a^{15}b^{21}$

В такого рода операциях с одночленами довольно легко ошибиться. Вот почему мы рекомендуем вам попрактиковаться с упражнениями, которые мы пошагово решили на нашем сайте. Вы быстро их найдете, выполнив поиск в поисковой системе вверху справа.

Числовое значение монома

Числовое значение монома — это результат, полученный путем замены переменных монома на определенные значения.

Например, если у нас есть следующий моном:

$5x^2$

Если мы хотим найти числовое значение предыдущего монома для

$x=2$

вам нужно заменить букву

$x$

монома на 2 и решаем полученные операции:

$5\cdot 2^2= 5 \cdot 4 = 20$

Значит, числовое значение монома

$5x^2$

Для

$x=2$

равно 20.

Вы также можете определить числовое значение мономиальной многопеременной. Например, если у нас есть следующая бивариантная или, другими словами, моном с двумя переменными:

$3x^4y$

Чтобы вычислить численное значение вышеуказанного монома, когда

$x$

стоит 1 е

$y$

равно -2, мы заменяем буквы на соответствующие значения:

$3\cdot 1^4\cdot (-2)= 3 \cdot 1 \cdot (-2) = -6$

Таким образом, численное значение монома задачи для

$x=1$

$y=-2$

возвращает -6.

Мономы и полиномы

Наконец, знайте, что многочлены можно образовывать из мономов:

Полином — это группа двух или более мономов.

$P(x)= 4x^5+3x^2-7x$

Например, предыдущий многочлен получается в результате сложения (или вычитания) трех разнородных мономов.

Из любопытства, когда многочлен имеет только 2 монома, его называют биномом . А когда многочлен имеет ровно три монома, он называется трехчленом .

Если вы хотите узнать больше о полиномах, вы можете посетить главную страницу Интернета, где мы объясняем все, что вам нужно знать о полиномах.