Вы наверняка слышали о множестве мнимых чисел или мнимой единице измерения. Это математическое понятие, возникающее из математической необходимости выражать числа, не принадлежащие действительным числам .
Что такое мнимые числа?
Мнимые числа – это числа, которые при возведении в квадрат дают отрицательное число . Следовательно, это значения, эквивалентные квадратному корню из отрицательного числа. Например, мнимая единица (число i) равна квадратному корню из -1.
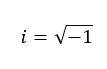
Эти числа не относятся к действительным числам, поскольку в вещественном множестве отрицательные корни не могут быть разрешены. В этом и заключается важность воображаемой обстановки. Этот набор был изобретен для того, чтобы иметь возможность иметь дело с отрицательными корнями и решать все те уравнения и квадратичные задачи, которые «не имеют решения», потому что они дают нам отрицательный корень.
Чтобы избежать путаницы, важно различать мнимые числа и комплексные числа . Комплексы – это числа, состоящие из действительного и мнимого чисел . Следовательно, воображаемые представляют собой подкатегорию комплексов, не имеющих реальной части. В следующей таблице вы сможете лучше оценить различия.
| комплексное число | королевская вечеринка | часть воображения | Описание |
| 4+7и | 4 | 7и | Сложный |
| 3 | 3 | 0 | чистый королевский |
| 2я | 0 | 2я | Чистое воображение |
Чтобы закончить размещение этого цифрового набора, мы можем визуализировать на следующем изображении структуру всех наборов. Как мы видим, комплексные числа охватывают все типы чисел , которые, в свою очередь, можно разделить на действительные числа и чисто мнимые числа (именно с ними мы и имеем дело в этой статье).

Примеры мнимых чисел
Из мнимой единицы (i) мы можем вывести другие мнимые числа. Вам просто нужно применить следующую формулу:
м = ри
Где m — мнимое число, r — действительное число, а i — мнимая единица. На следующем изображении вы можете увидеть, как мы получаем разные образы из отрицательных корней.
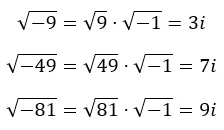
Фактически, мы можем экстраполировать это к следующему выражению:
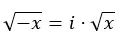
Свойства мнимых чисел
Мнимые числа обладают рядом очень интересных свойств . О некоторых мы уже говорили в начале этой статьи, а о других нет:
- Воображаемые представления не принадлежат к множеству реальностей, поскольку представляют собой числа, которые физически не существуют и не могут быть представлены в нашей реальности.
- Это значения, эквивалентные отрицательным корням.
- Их можно изобразить графически на воображаемой линии.
- Мнимые степени (эту концепцию мы объясним в следующем разделе) очень помогают упростить числовые вычисления с использованием мнимых значений.
- Формула Эйлера — это выражение, позволяющее соотносить мнимые числа с действительными.
Действия с мнимыми числами
Теперь, когда вы знаете все важные характеристики мнимых чисел, пришло время научиться решать действия с ними. Чтобы оперировать мнимыми значениями , вы должны выполнить те же шаги, которые вы выполняете для работы с реальными значениями, за исключением того, что вы должны принять во внимание одно понятие: мнимые силы.
творческие способности
У мнимых чисел есть очень интересное свойство, которое возникает, когда вы умножаете мнимую единицу на себя. То есть это происходит, когда вы создаете силы мнимого единства . Если записать полномочия, как в следующем списке, можно обнаружить закономерность:
я 0 = 1
я 1 = я
я 2 = я · я = ( √ -1) · ( √ -1) = -1
я 3 = я 2 я = (-1) я = -я
я 4 = я 2 я 2 = (-1) (-1) = 1
Знание этого понятия значительно облегчит нам решение операций с мнимыми числами, поскольку мы сможем упростить сложные операции и сделать их немного легче. Кроме того, в этих способностях хорошо то, что они повторяются бесконечно. Мы сможем увидеть это, если добавим еще несколько полномочий:
я 5 = я
я 6 = -1
я 7 = -я
я 8 = 1
и т. д.
И с отрицательными силами то же самое происходит.
Арифметические действия с мнимыми числами
Далее мы дадим вам пример каждой основной арифметической операции, чтобы вы могли увидеть решенные вычисления с мнимыми числами.
- Сложение мнимых чисел: это точно так же, как сложение действительных чисел, только не забудьте добавить i.
4и + 3и = 7и
- Вычитание мнимых чисел: Вычитания также решаются так же, как и в реальном множестве.
4i – 3i = я
- Умножение мнимых чисел: в этом случае мы должны иметь в виду мнимые степени, о которых мы упоминали ранее.
3i 4i = 12 i 2 = 12 (-1) = -12
- Деление мнимых чисел: при этом типе деления мы также должны быть бдительными, на случай, если мы столкнемся с мнимой силой, которая позволяет нам упростить операцию.
12i ÷ 4i = 3
Уравнения с мнимыми числами
Как мы уже говорили, когда мы решаем уравнения вещественного множества, иногда мы получаем отрицательные корни и, следовательно, уравнения «не имеют решения» . Но теперь, когда мы знаем воображаемое, мы можем решить эти уравнения. Давайте посмотрим пример:
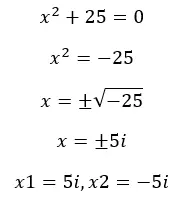
Для чего используются мнимые числа?
Мнимые числа возникают из-за необходимости иметь возможность выражать значения, находящиеся за пределами реального множества. Поэтому на первый взгляд может показаться, что полезных приложений у них не так много . Но правда в том, что все совсем наоборот. Потому что, когда мы объединяем их с действительными, мы получаем комплексные числа.
И у них есть много применений. Их используют для изучения переменного тока (поскольку он имеет отрицательные значения), его применение также очень широко распространено в области волн (что имеет приложения в физике, телекоммуникационной электронике и квантовой механике). Среди многих других применений.
Кроме того, часто случается, что когда вы решаете квадратное уравнение , значение дает вам отрицательный корень, и вы не можете действовать… С помощью воображаемых уравнений вы можете их решить . Итак, в заключение можно сказать, что это набор, который позволяет нам расширить наши более абстрактные знания.