На этой странице вы узнаете, что такое метод Гаусса-Жордана и как решить систему уравнений с помощью метода Гаусса. Кроме того, вы также найдете примеры и решенные упражнения для систем с помощью метода Гаусса, чтобы вы могли в совершенстве попрактиковаться и понять его.
Что такое метод Гаусса?
Метод Гаусса-Жордана — это процедура, используемая для решения систем уравнений с тремя неизвестными, то есть следующим образом:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-088146ef83bbd007e82aca8189434c25_l3.png)
Целью метода Гаусса является преобразование исходной системы уравнений в ступенчатую систему , то есть систему, в которой каждое уравнение имеет на одно неизвестное меньше, чем предыдущее:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10926b0856ae512c737ae924bd9413a1_l3.png)
Однако для этого необходимо сначала знать, как выразить систему уравнений в матричной форме и какие преобразования разрешены в этой матрице. Итак, мы объясним эти две вещи раньше, а затем увидим, как использовать процедуру метода Гаусса .
Системно-расширенная матрица
Прежде чем увидеть, как решается система, вы должны знать, что систему уравнений можно выразить в виде матрицы: коэффициенты
![]()
в первом столбце помещаются коэффициенты
![]()
во втором столбце коэффициенты
![]()
в третьем столбце и числа без неизвестных в четвертом столбце.
Например:
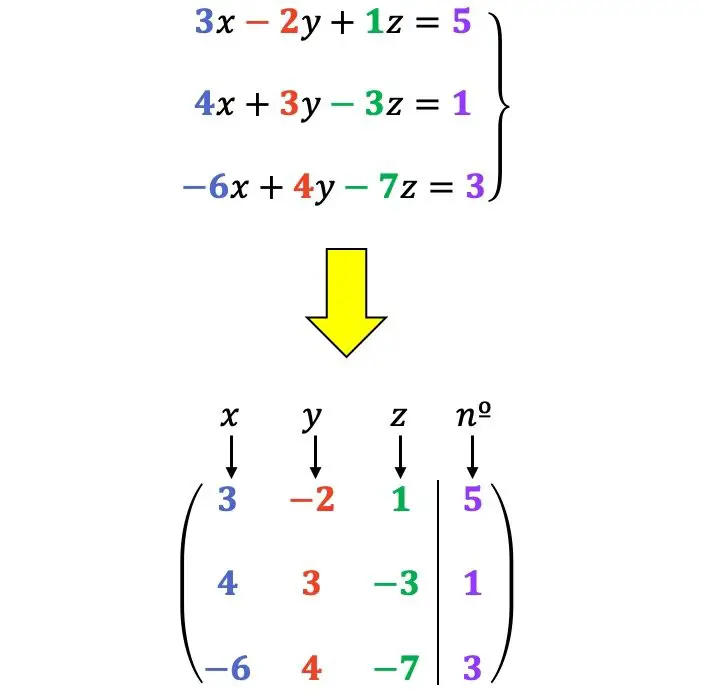
Разрешенные преобразования строк
Чтобы преобразовать систему уравнений в масштабированную систему, над матрицей, связанной с системой, можно выполнить одну из следующих операций:
- Измените порядок строк в матрице.
Например, мы можем изменить порядок строк 2 и 3 матрицы:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ee0e251559ef9dfd02c9b0105f934af8_l3.png)
- Умножьте или разделите все члены подряд на число, отличное от 0.
Например, мы можем умножить строку 1 на 4 и разделить строку 3 на 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e1f081c9056075ede064b2e5c9e4193_l3.png)
- Замените строку суммой той же строки плюс другой строки, умноженной на число.
Например, в следующей матрице мы добавляем строку 2 к строке 3, умноженную на 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-04417e2094ac05c7a374334c55197f36_l3.png)
Как решить систему уравнений методом Гаусса?
Рассмотрим теперь на примере процедуру решения системы уравнений методом Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e6e829301e6730c9e27f9c0a30de2e_l3.png)
Первое, что нужно сделать, это расширенная матрица системы :
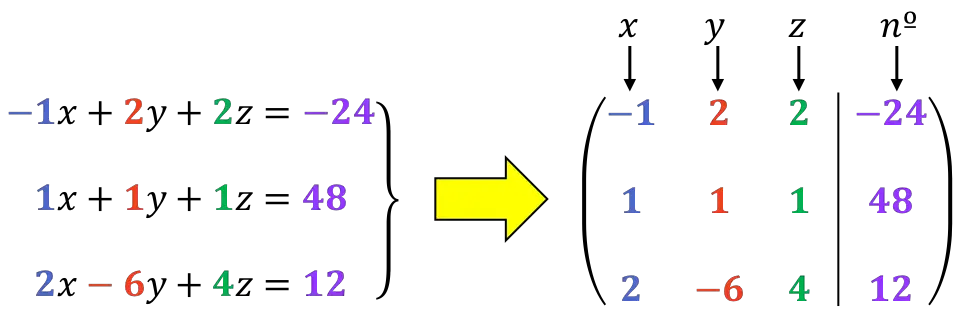
Как мы увидим позже, лучше, чтобы первая цифра первой строки была 1. Поэтому мы изменим порядок строк 1 и 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b45e0f757ca2880442314f6a4800697b_l3.png)
Цель метода Гаусса — сделать числа ниже главной диагонали равными 0 . То есть нам нужно преобразовать красные цифры в 0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-28164ac6b48d32c09b4725548c0633f6_l3.png)
Чтобы исключить эти числа, нам необходимо выполнить соответствующие преобразования строк.
Например, -1, который является первым элементом второй строки, является отрицательным значением 1, первого элемента первой строки. Следовательно, если мы добавим первую строку ко второй строке, -1 будет исключено:

Итак, если мы сделаем эту сумму, мы получим следующую матрицу:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b106306b92bfc3e99d602c22d5198bd_l3.png)
Таким образом нам удалось преобразовать -1 в 0.
Теперь мы собираемся преобразовать цифру 2. Если вы заметили, цифра 2, которая является первым элементом в третьей строке, в два раза больше 1, первого элемента в первой строке. Следовательно, если мы добавим первую строку, умноженную на -2, к третьей строке, 2 будет исключено:
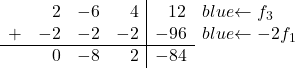
Таким образом, мы получаем следующую матрицу:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-36b2fdf8de855cf35049ecefcf7c1da5_l3.png)
Таким образом нам удалось превратить 2 в 0.
Все, что нам нужно сделать сейчас, это преобразовать -8 в 0. Для этого мы умножаем третью строку на 3 и добавляем вторую строку, умноженную на 8:
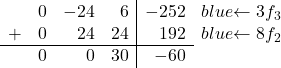
Таким образом, мы получаем следующую матрицу:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e2324629222c746a9021ce05ba7d54d_l3.png)
И с помощью этих преобразований мы получили, что все числа ниже главной диагонали равны 0. Итак, теперь мы можем решить систему уравнений.
Теперь нам необходимо преобразовать матрицу в систему уравнений с неизвестными . Для этого помните, что первый столбец соответствует
![]()
, второй столбец
![]()
, третий столбец
![]()
и последний столбец — числа без неизвестных:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f90de9d9f5a06959a2d4aebf05f4758_l3.png)
И, наконец, для решения системы нам необходимо решить неизвестные уравнений снизу вверх. Поскольку последнее уравнение имеет только одно неизвестное, мы можем его решить и найти его значение:
![]()
![]()
![]()
Теперь, когда мы знаем, что такое z, если подставить его значение во второе уравнение, мы сможем найти значение
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и стираем
![]()
:
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Решаемые задачи систем уравнений методом Гаусса-Жордана
Упражнение 1
Решите следующую систему уравнений методом Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854043b0e7e3e2166593dcf5c645bfa0_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b6369a58b91f31bf4c8bc212ccf68c6_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Поэтому мы выполняем операции со строками, чтобы отменить два последних члена первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd42dcf61aebc4c67de13e09dff72f4b_l3.png)
Теперь удалим последний элемент из второго столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-13945337848a6f1badf6efe249951124_l3.png)
Когда все числа ниже главной диагонали равны 0, мы можем решить систему уравнений. Для этого еще раз выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f068c276aae018a668cc005bcad3e641_l3.png)
И решаем неизвестные уравнения снизу вверх. Сначала решим последнее уравнение:
![]()
![]()
Теперь подставим значение z во второе уравнение, чтобы найти значение y:
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и находим x:
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 2
Найдите решение следующей системы уравнений, используя метод Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0595899b8137f769c74fce1b21286b_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e2a16b6d1451520bd8898675c022dc2_l3.png)
Применить метод Гаусса проще, если первое число в первой строке равно 1. Поэтому мы изменим порядок строк 1 и 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef7e2e42d0eecb0395afb7c8311b2ade_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Итак, мы выполняем операции со строками, чтобы заменить два последних элемента первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-40baaee3bbde9ed1577e00bc1c3b338f_l3.png)
Теперь преобразуем последний элемент второго столбца в ноль:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f328906485bfe6ee77833c04869e1240_l3.png)
Как только все числа ниже главной диагонали равны 0, мы можем решить систему уравнений. Для этого еще раз выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7e129715c720218a5cb25ef07442442_l3.png)
И решаем неизвестные уравнения снизу вверх. Сначала решим последнее уравнение:
![]()
![]()
Теперь подставим значение z во второе уравнение, чтобы найти значение y:
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и находим x:
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 3
Рассчитаем решение следующей системы уравнений методом Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4301eae3179543fbdee7568e8f88aa4c_l3.png)
Первое, что нам нужно сделать, это расширенную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0d96160d6670e817dd39f61816e1e6e_l3.png)
Теперь нам нужно сделать все числа в родительском массиве равными 0.
Итак, мы выполняем операции со строками, чтобы заменить два последних элемента первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-87853177b6be449178c24e414dc0865a_l3.png)
Теперь преобразуем последний элемент второго столбца в ноль:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4105ceb64b201c532109f8639bdefde_l3.png)
Как только все числа ниже главной диагонали равны 0, мы можем решить систему уравнений. Для этого еще раз выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-faae83295a3f7b3d8b6d76f78d56fac6_l3.png)
И решаем неизвестные уравнения снизу вверх. Сначала решим последнее уравнение:
![]()
![]()
Теперь подставим значение z во второе уравнение, чтобы найти значение y:
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и находим x:
![]()
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()
Упражнение 4
Решите следующую систему уравнений с тремя неизвестными методом Гаусса:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b005b2eda0d63c7130f2f5531c2ae4a0_l3.png)
Прежде чем применять метод Гаусса, нам необходимо расположить систему уравнений так, чтобы все неизвестные находились слева от уравнения, а числа — справа:
![Rendered by QuickLaTeX.com \left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0ca77b625e8f9e235ce8da4e4008df_l3.png)
После упорядочения системы строим разработанную матрицу системы:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b88e3ff141b847028a55ba4b46b8e870_l3.png)
Так как все числа в первой строке четные, то перед работой со строками разделим первую строку на 2. Так как это облегчит расчеты:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05235526cd8e44c16749606bfe8976c_l3.png)
Теперь нам нужно сделать все числа ниже основного массива равными 0.
Итак, мы выполняем операции со строками, чтобы заменить два последних элемента первого столбца:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3da82815d14fdfae0f61a8e1747fb9fe_l3.png)
Как и раньше, поскольку все числа в последней строке кратны 9, для облегчения расчетов разделим ее на 9:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-342000d19a7bd19e055a39695c79cb49_l3.png)
Теперь преобразуем последний элемент второго столбца в ноль:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2158e7f439f677617bb8a40695fb5711_l3.png)
Как только все числа ниже главной диагонали равны 0, мы можем решить систему уравнений. Для этого еще раз выразим матрицу в виде системы уравнений с неизвестными:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ea162e98aa70f8d56ffba28438a9de2a_l3.png)
И решаем неизвестные уравнения снизу вверх. Сначала решим последнее уравнение:
![]()
![]()
Теперь подставим значение z во второе уравнение, чтобы найти значение y:
![]()
![]()
![]()
![]()
![]()
И то же самое делаем с первым уравнением: подставляем значения остальных неизвестных и находим x:
![]()
![]()
![]()
![]()
Таким образом, решение системы уравнений имеет вид:
![]()