Magic Squares — это математическая игра-головоломка, которая в увлекательной и увлекательной форме тренирует наши вычислительные навыки. Вот почему это один из лучших ресурсов для преподавания математики юным школьникам.
Что такое магический массив и как он разрешается?
Магический квадрат — это своего рода таблица или матрица, состоящая из различных ячеек, в которых записаны целые числа . Но ни в коем случае их нельзя устанавливать; необходимо соблюдать ряд правил:
- Все магические суммы (суммы всех значений любой горизонтальной, вертикальной или диагональной линии) всегда должны давать значение, эквивалентное магической константе (это единственное значение).
- Ни одно число не может повторяться дважды.
- Вы можете использовать только последовательные числа (например, от 1 до 9) или числа, следующие за определенной серией, например: нечетные числа, кратные 5 и другие.
Также важно подчеркнуть, что мы можем проводить различные классификации квадратов в зависимости от их структуры. Первый соответствует степени квадрата , которая эквивалентна количеству ячеек в строке или столбце. А второй – по типу степени таблицы ( четные или нечетные числа). Исходя из этих различий, мы можем распределить все квадраты по разным категориям, хотя мы подробно остановимся на этом позже.
Как решить магические квадраты?
Чтобы решить эту математическую игру, мы можем использовать два разных метода: использовать геометрию или вычислить магическую константу. Обе процедуры одинаково действенны, хотя одна позволяет быстрее добиться результата, а другая требует больше времени и рассуждений . Далее мы объясним оба метода, чтобы вы могли выбрать тот, который вам больше нравится, и лучше адаптироваться к каждой ситуации.
Какова формула магических квадратов?
Первый метод заключается в вычислении магической константы , для чего мы должны использовать следующую формулу: n(n 2 +1)/2, где n — степень квадрата. И как только мы получим это значение, останется только попробовать разные комбинации чисел, которые позволят нам приравнять магические суммы всего квадрата к константе. Другими словами, нам нужно формировать комбинации чисел, в сумме дающие значение константы, чтобы вся картина была сбалансированной.
Как решить магические квадраты с помощью геометрии?
Во-вторых, мы можем решать магические квадраты, используя геометрию . Хотя следует отметить, что этот метод очень прост и не требует от вас тренировки навыков расчета, так как носит чисто методический характер. При этом мы объясним процедуру решения квадратов четного и нечетного порядка.
Как решить магические квадраты с нечетными числами?
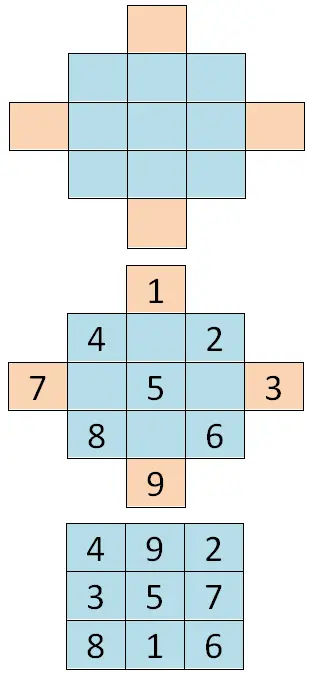
Чтобы решить этот первый случай, вы должны добавить ячейки в исходную таблицу, чтобы получился своего рода ромб. Затем нам нужно написать все последовательные числа, начиная с первой цифры ряда (в нашем случае 1), и мы будем следовать диагоналям ромба . Наконец, нам нужно «удвоить» цифру, поэтому значения внешних ячеек уходят в противоположную сторону. Итак внешние ячейки вертикальной оси пересекаются, затем то же самое происходит и с ячейками горизонтальной оси, ниже вы можете увидеть пример:
Как решить магические квадраты четного порядка?
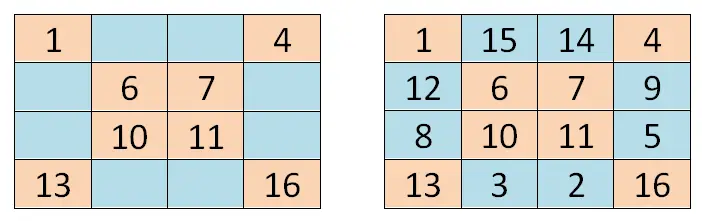
Чтобы решить магический квадрат четного порядка (магические квадраты, имеющие четное количество строк и столбцов), мы можем прибегнуть к методу, несколько отличающемуся от предыдущего, но также основанному на геометрии. Начнем с написания первого номера серии (в нашем случае 1) в верхнем левом углу. Затем мы пройдем две основные диагонали и запишем значения, соответствующие положению каждого прямоугольника.
После того, как мы записали две основные диагонали, нам нужно будет разместиться в первом пустом поле, начиная с правого нижнего угла (в нашем случае это поле 15). Туда же мы запишем второе значение ряда и остальные значения запишем по порядку (от меньшего к большему), заполняя ячейки справа налево и снизу вверх . Чтобы было понятнее, вы можете сориентироваться по изображению, которое мы вам покажем ниже:
Как построить магические квадраты?
Чтобы самостоятельно построить магические квадраты, мы можем выполнить несколько процедур, среди которых выделим две. Следует отметить, что каждый из них будет использоваться для создания квадратов разных типов, поэтому вам придется тщательно выбирать метод в зависимости от квадрата, который вы хотите создать:
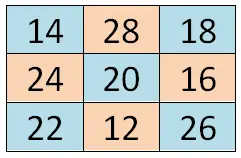
Сиамский метод
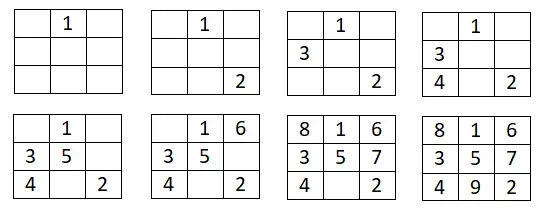
Этот первый метод довольно прост и помогает нам строить нечетные магические квадраты любого размера. Процедура очень проста: по сути, мы пишем первый номер серии в центральном поле первой строки. Отсюда мы вернемся по порядку в выбранной нами арифметической прогрессии, записывая следующее число вверх и вправо . Однако если эта позиция находится за пределами нарисованного квадрата, нам придется перейти к последней строке или столбцу. И если у нас получится полный квадрат, нам придется спуститься на один квадрат вниз от последнего числового квадрата, который мы ввели, и тогда мы продолжим в том же духе.
Ниже вы можете увидеть пример 3х3:
Метод Стрейчи для магических квадратов
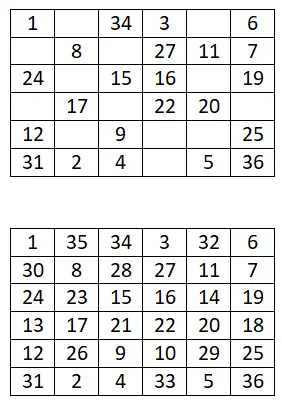
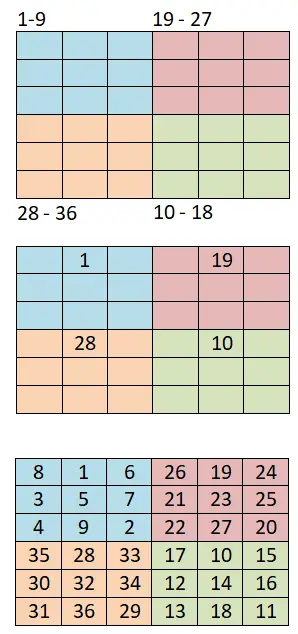
Чтобы сгенерировать магические квадраты порядка 4k + 2 пар , мы будем использовать другой метод, основанный на предыдущем (сиамский метод) и который также очень прост. Ниже вы можете увидеть шаги и рабочий пример магического квадрата 6×6:
- Разделение на меньшие квадраты. Первое, что нам нужно сделать, это разделить доску на более мелкие квадраты. Например, если у нас есть доска 6х6, нам нужно будет сделать четыре равных квадранта из квадратов 3х3.
- Используйте сиамский метод: затем мы назначим диапазон чисел каждому маленькому квадранту, например, если мы начнем последовательность с 1, диапазоны будут такими: 1–9 (первый), 10–18 (четвертый), 19–27. (второй) и 28-36 (третий).
LUX-метод Конвея для магических квадратов
Мы будем использовать последнюю систему, когда хотим сгенерировать магические квадраты порядка 4n + 2 , где n — натуральное число. Итак, процедура, которой мы будем следовать для создания квадратов этого стиля, следующая:
- Создание таблицы или матрицы: начнем с создания матрицы степени 2n + 1, где n — натуральное число. Благодаря этому мы сможем спроектировать стол, учтем его степень, а затем приступим к проектированию.
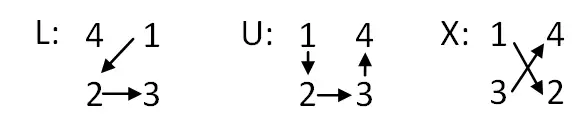
- Расположение букв: как только таблица построена, вам нужно будет написать сверху вниз: n + 1 строка L, 1 строка U и n – 1 строка X. А затем вам придется поменять местами буквы U. посередине с буквой L вверху.
- Поменяйте местами буквы на числовые значения. Теперь нам нужно будет заменить буквы группами из четырех последовательных цифр. В зависимости от буквы мы придадим цифрам тот или иной порядок. Объяснено ниже:
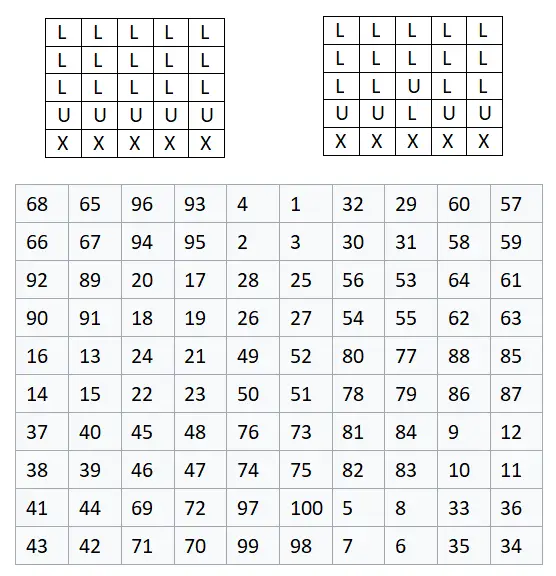
Мы начнем с построения матрицы 5×5 , поэтому n = 2, поскольку: 2n + 1 = 2 · 2 + 1 = 5. Это означает, что в конечном итоге матрица будет иметь размер 10×10, потому что, как мы As как мы уже говорили, каждая ячейка, содержащая букву, эквивалентна группе из четырех чисел, т.е. матрице 2×2. Ниже вы можете увидеть готовый пример, в котором мы заменили каждую букву группой из четырех цифр в порядке, показанном на изображении:
упражнения с магическими квадратами
Далее мы предлагаем вам несколько неполных магических квадратов, которые вам придется заполнить самостоятельно благодаря концепциям, которые мы объяснили в этой статье. Помните, что вы можете использовать любой из описанных методов. Дополнительно нужно учитывать, что 1 может быть не первым числом в серии, хотя в объявлении она будет поставлена. А когда вы закончите одно из упражнений, вы сможете увидеть решение под утверждением.
магический квадрат 3×3
Постройте магический квадрат 3×3 только с нечетными числами:
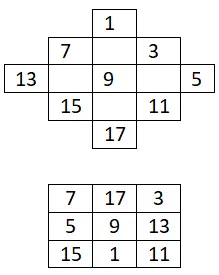
магический квадрат 4×4
Заполните следующий магический квадрат 4×4:
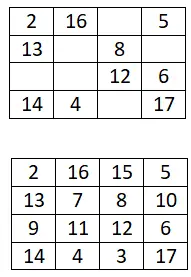
магический квадрат 5×5
Заполните следующий магический квадрат 5×5:
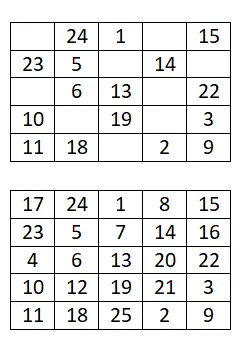
магический квадрат 6×6
Заполните следующий магический квадрат 6×6: