В этой статье вы найдете объяснение аффинной функции и линейной функции, а также различий, существующих между этими двумя типами функций. Кроме того, вы увидите примеры того, как построить график аффинной функции и линейной функции и как вычислить их выражения из двух точек. Наконец, вы сможете тренироваться, выполняя несколько упражнений, решая шаг за шагом.
Что такое аффинная функция и линейная функция?
Определения аффинной функции и линейной функции следующие:
Аффинная функция — это полиномиальная функция первой степени, то есть функция, которая, представленная на графике, представляет собой прямую линию. Сопутствующие функции следующие:
![]()
Золото
![]()
это наклон линии и
![]()
Это точка пересечения по оси Y, то есть точка пересечения функции с вертикальной осью.
В математике аффинные функции также называются линейными преобразованиями в контексте линейной алгебры.
Линейная функция — это аффинная функция, не имеющая независимого члена. Следовательно, формула для линейных функций имеет вид:
![]()
Золото
![]()
это наклон линии.
Область определения и диапазон (или диапазон) линейной функции и аффинной функции являются действительными числами:
![]()
![]()
В чем разница между линейной функцией и аффинной функцией?
Теперь, когда вы познакомились с понятиями линейной функции и аффинной функции, вы заметили, что они очень похожи друг на друга. Однако очень важно следующее различие между ними:
Единственное различие между линейной функцией и аффинной функцией состоит в том, что линейная функция не имеет независимого члена, в то время как аффинная функция всегда имеет коэффициент при пересечении (n), отличный от нуля (0).
Линейная функция
![]()
линейная функция
![]()
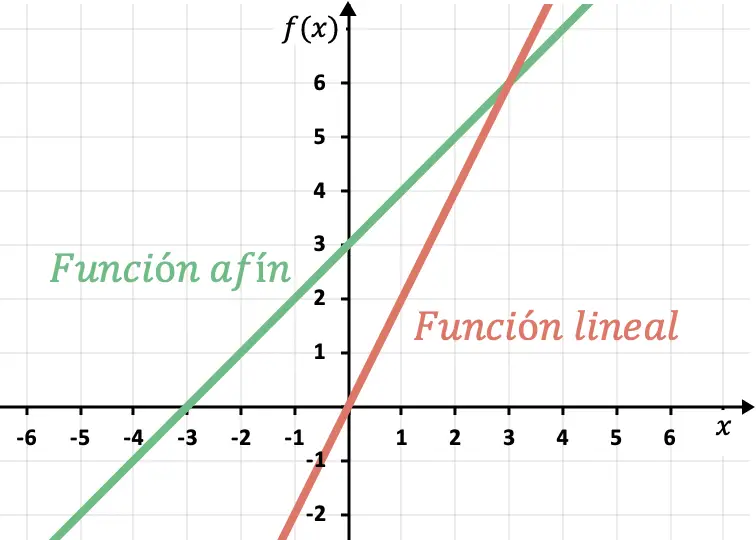
Это означает, что линейная функция всегда проходит через начало координат , точку (0,0). С другой стороны, аффинная функция никогда не пройдет через эту точку, поскольку ее точка пересечения отлична от 0.
Наклон и точка пересечения по оси Y линейной или аффинной функции
В этом разделе мы проанализируем пример аффинной или линейной функции, чтобы понять значение терминов.
![]()
И
![]()
или, другими словами, наклон и точка пересечения по оси Y.
- Определите выражение функции, изображенной на графике, и классифицируйте ее как линейную или аффинную функцию.
Эти типы функций следуют следующему выражению:
![]()
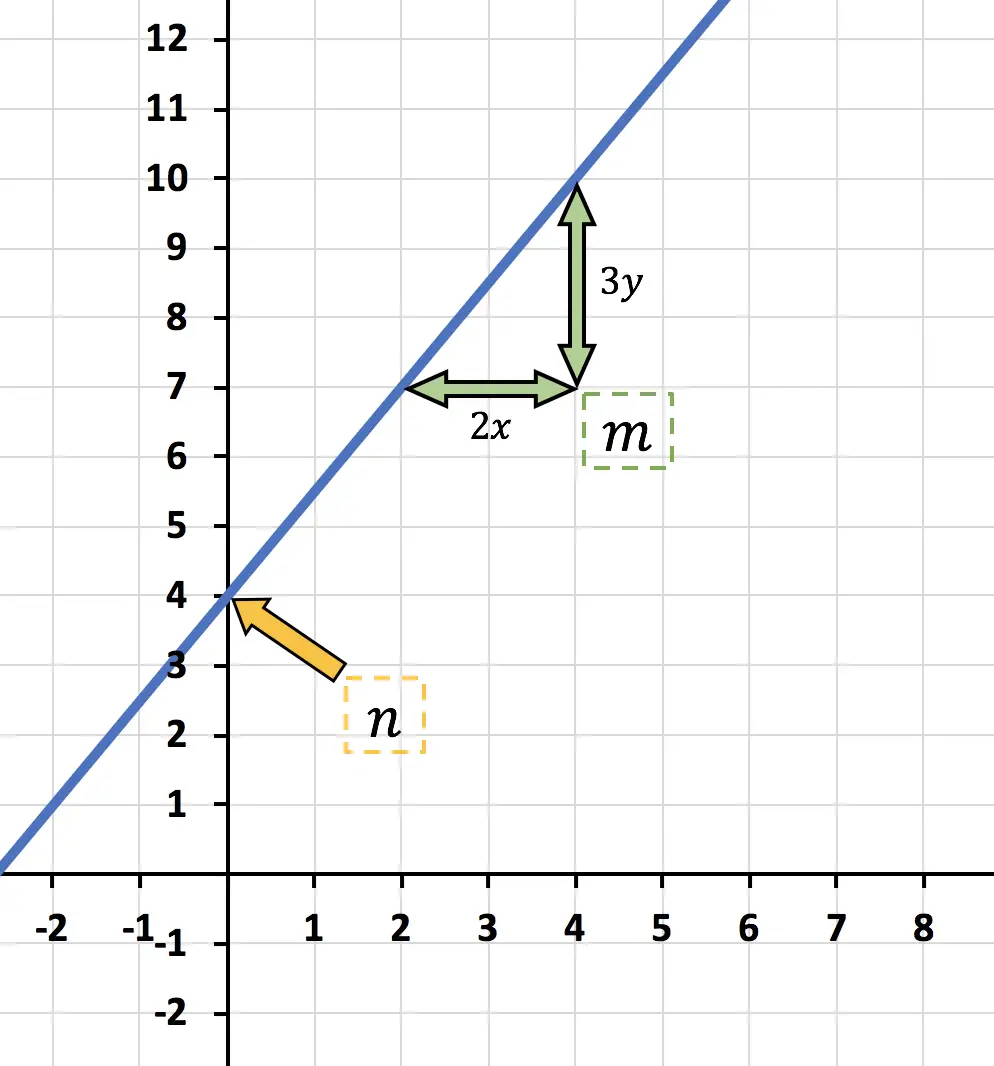
![]()
Это точка пересечения оси Y, т. е. точка пересечения функции с вертикальной осью Y. Итак, в этом случае:
![]()
С другой стороны,
![]()
это наклон линии. Y можно рассчитать, разделив разницу y между двумя точками на разницу х между этими же двумя точками:
![]()
![]()
говорит «на сколько y увеличивается для каждого x» , поэтому в этом случае функция «3y увеличивается для каждых 2x» .
В заключение, выражение для аффинной функции, представленное на графике, имеет вид:
![]()
Кроме того, поскольку точка пересечения по оси Y не равна нулю, это аффинная функция .
Ниже мы покажем вам больше примеров линейных и аффинных функций, чтобы вы лучше поняли:
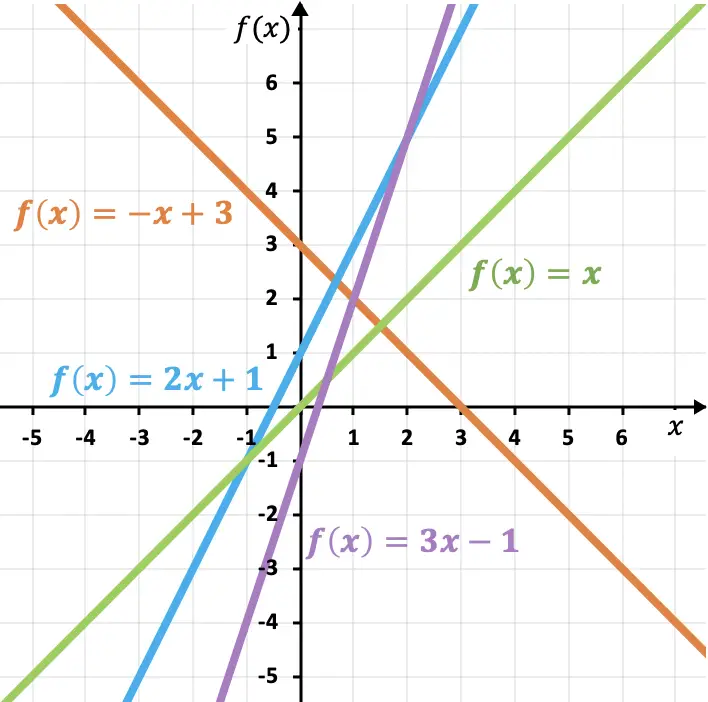
Как видно из этих примеров, чем больше наклон, тем круче линия и, следовательно, тем больше функция. Аналогично коэффициент наклона определяет рост или убывание функции:
- Если наклон положительный, функция возрастает , то есть увеличивается с увеличением x .
- Если наклон отрицательный, функция убывает , то есть уменьшается с увеличением x .
Кроме того, вы также можете определить, параллельны или перпендикулярны две линии по их наклонам:
- Когда две линии имеют одинаковый наклон, они параллельны , то есть не пересекаются ни в одной точке или полностью идентичны.
![]()
- С другой стороны, две линии перпендикулярны , то есть пересекаются под вертикальным углом (90°), если их наклоны соответствуют следующему соотношению:
![]()
Пример представления аффинной или линейной функции
Давайте посмотрим, как построить график функции первой степени на примере.
- Постройте график следующей аффинной функции:
![]()
Первое, что нам нужно сделать, это создать массив значений. Для этого мы предоставляем нужные нам значения
![]()
для получения значений
![]()
:
![]()
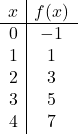
Хотя таблицы значений с двумя точками достаточно, мы можем сделать больше точек, чтобы убедиться в ее правильности.
После того, как мы создали таблицу значений, наносим точки на график:
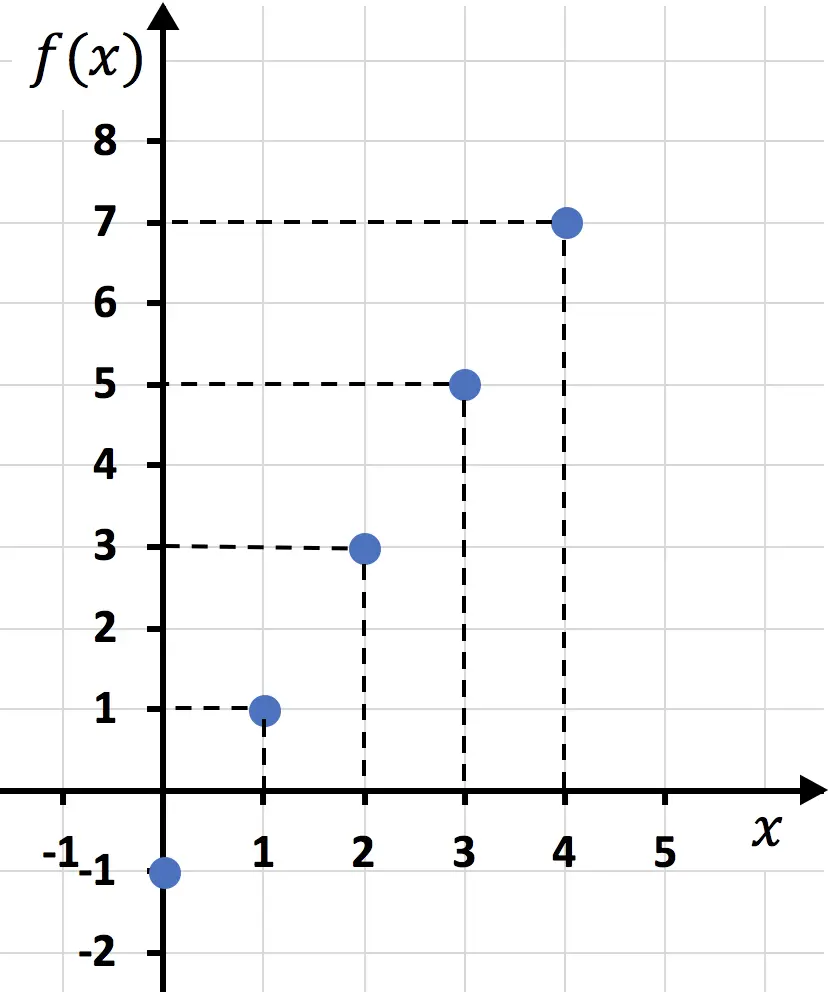
И наконец, соединяем точки и проводим линию:
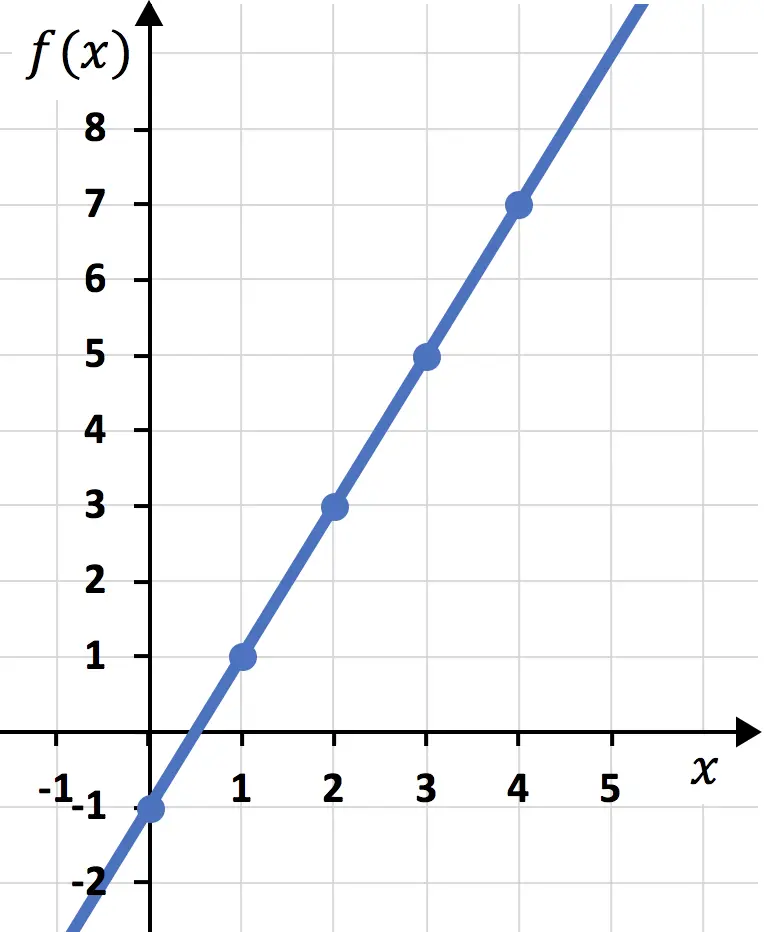
Таким образом, мы уже представили функцию на графике. Как видите, это не сложно, просто нужно сначала составить таблицу значений, а затем нанести точки на график.
Как вычислить линейную или аффинную функцию по двум точкам
Теперь посмотрим, как найти линейную или аффинную функцию из двух точек на примере:
- Вычислите линейную функцию, удовлетворяющую условию
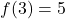
и пройти через точку
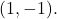
Прежде всего,
![]()
Это означает, что функция проходит через точку
![]()
.
Следовательно, поскольку у нас есть две точки, через которые проходит функция, мы можем вычислить наклон
![]()
функция:
Учитывая два момента,
![]()
И
![]()
, склон
![]()
функции вычисляется:
![]()
В нашем случае функция проходит через точки
![]()
И
![]()
. Итак, наклон
![]()
функции:
![]()
Таким образом, функция будет иметь вид:
![]()
Как только мы узнаем
![]()
мы можем разгадать тайну
![]()
. Для этого подставим в уравнение координаты точки, принадлежащей функции. Например пункт (3.5):
![]()
Решаем полученное уравнение:
![]()
![]()
![]()
![]()
Таким образом, линейная функция:
![]()
Решенные упражнения на линейные и аффинные функции
Упражнение 1
Определите наклон и начало координат следующей аффинной функции:
![]()
Линейная функция имеет вид
![]()
Таким образом, наклон функции — это число, которое сопровождает x , которое в данном случае равно -5:
![]()
А точка пересечения по оси Y — это независимый член, который в данном случае равен -2:
![]()
Упражнение 2
Постройте график следующей аффинной функции:
![]()
Сначала мы придаем значения
![]()
создать таблицу значений:
![]()
![]()
![]()
![]()
![]()
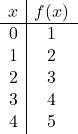
А затем представляем точки из таблицы значений на графике и проводим линию:

Упражнение 3
Постройте на графике следующую аффинную функцию:
![]()
Сначала мы придаем значения
![]()
создать таблицу значений:
![]()
![]()
![]()
![]()
![]()
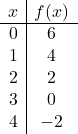
И наконец, представляем точки из таблицы значений на графике и проводим линию:
Упражнение 4
Найдите выражение для аффинной функции, проходящей через точки (2,3) и (0,1).
Функция проходит через точки (2,3) и (0,1), поэтому наклон функции равен:
![]()
И функция будет иметь вид:
![]()
Зная m, мы можем вычислить n . Для этого нам необходимо подставить в уравнение координаты точки, принадлежащей функции. Например пункт (2,3):
![]()
![]()
Теперь нам необходимо решить полученное уравнение:
![]()
![]()
Таким образом, функция соответствует следующему выражению:
![]()
Упражнение 5
Постройте график следующей аффинной функции:
![]()
Сначала мы придаем значения
![]()
создать таблицу значений:
![]()
![]()
![]()
![]()
![]()

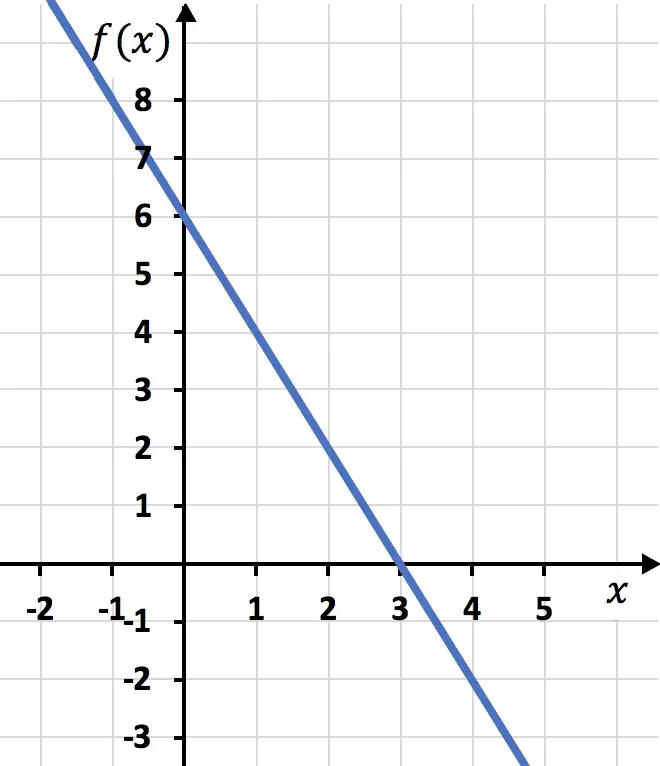
А затем представляем точки из таблицы значений на графике и проводим линию:

Упражнение 6
Вычислите линейную функцию, удовлетворяющую следующим двум условиям:
![Rendered by QuickLaTeX.com \begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3d1692f49f622f3167c7b58da6553eb_l3.png)
Пусть это сбудется
![]()
Это означает, что функция проходит через точку (3,-2). И таким же образом,
![]()
Это означает, что функция проходит через точку (-1,6).
Итак, функция проходит через точки (3,-2) и (-1,6), поэтому ее наклон равен:
![]()
Таким образом, функция будет иметь вид:
![]()
И как только мы узнаем m, мы сможем вычислить n . Для этого подставим в уравнение координаты точки, принадлежащей функции. Например точка (3,-2):
![]()
И решаем полученное уравнение:
![]()
![]()
![]()
Таким образом, функция такова:
![]()
Упражнение 7
Найдите аффинную функцию, которую он выполняет.
![]()
и проходит через точку (3.5).
Пусть это сбудется
![]()
Это означает, что функция проходит через точку (1,6).
Таким образом, функция проходит через точки (1.6) и (3.5), и поэтому ее наклон равен:
![]()
Таким образом, функция будет иметь вид:
![]()
Зная термин m, мы можем вычислить коэффициент n . Для этого подставим в уравнение координаты точки, принадлежащей функции. Например точка (1,6):
![]()
Решаем полученное уравнение:
![]()
![]()
Помните, что для сложения дробей необходимо сначала привести их к общему знаменателю, а затем сложить числители:
![]()
![]()
![]()
Таким образом, функция такова:
![]()
Упражнение 8
Решите следующую задачу, связанную с линейными и аффинными функциями:
Магазин продает 40 единиц товара при цене 15 евро за единицу и 65 единиц при цене 10 евро за единицу.
- Рассчитайте функцию спроса на продукт, предполагая, что это аффинная функция.
- Сколько единиц будет продано, если цена будет установлена на уровне 12 евро за единицу?
Поскольку это аффинная функция, она будет иметь тип
![]()
Золото
![]()
будет цена за единицу продукции и
![]()
будут проданы единицы.
В пресс-релизе сообщается, что при цене 15 евро за единицу продается 40 единиц. Поэтому, как
![]()
это цена и
![]()
проданных единиц, должно соблюдаться следующее равенство:
![]()
А когда цена составляет 10 евро за единицу, продается 65 единиц. Итак, используя те же рассуждения:
![]()
Пусть это сбудется
![]()
Это означает, что функция проходит через точку (15.40). И
![]()
Это означает, что функция проходит через точку (10.65).
Таким образом, наклон функции равен:
![]()
Таким образом, функция будет иметь вид:
![]()
Зная m, мы можем вычислить n . Для этого подставим в уравнение координаты точки, принадлежащей функции. Например, точка (15:40):
![]()
И решаем полученное уравнение:
![]()
![]()
![]()
Таким образом, функция, которая связывает объем продаж с ценой, имеет вид:
![]()
С другой стороны, в функции
![]()
представляет цену. Следовательно, чтобы узнать, сколько единиц будет продано при цене 12 евро за единицу, мы должны рассчитать
![]()
![]()
![]()
![]()
Таким образом, если цена составит 12 евро за единицу , будет продано 55 единиц.