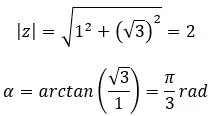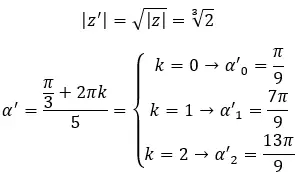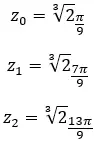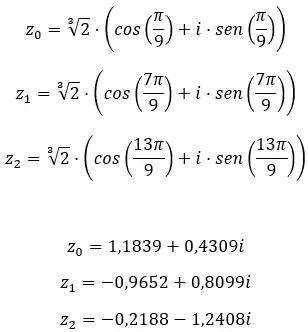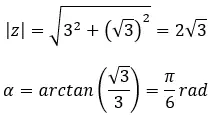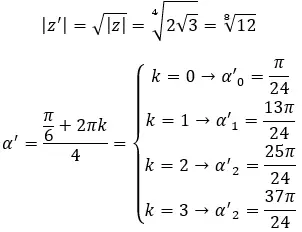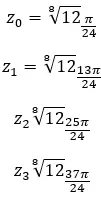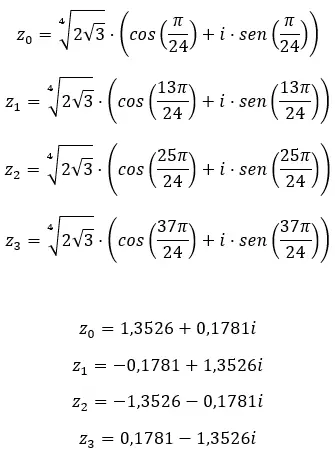Вычислить корни комплексных чисел довольно просто. Что ж, как только вы поймете процедуру, она станет довольно повторяющейся. Далее мы объясним это и приведем пример, чтобы вы могли научиться применять его в реальных упражнениях.
корни n-й степени из комплексных чисел
Понятие корня n-й степени эквивалентно произнесению корня порядка n, поэтому тот же метод используется для вычисления квадратного корня и корня пятой степени из комплексного числа. Конечно, количество решений будет меняться в зависимости от этого порядка.
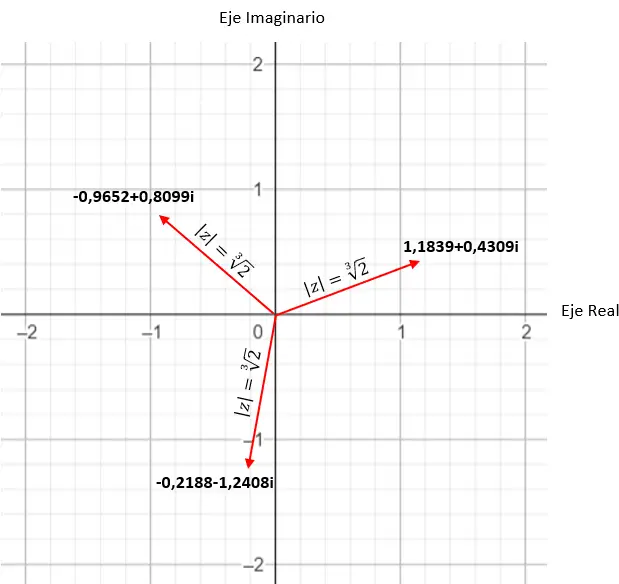
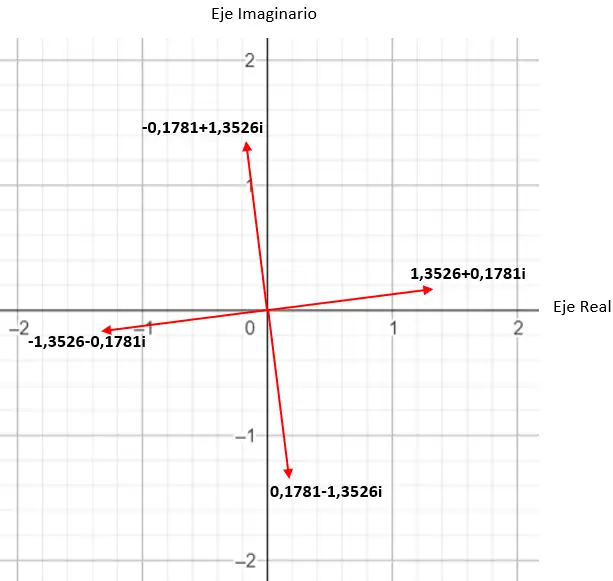
Например, если мы вычислим корень четвертой степени комплекса, мы получим 4 разных решения. А если выразить это в комплексной плоскости , то мы увидим, что образуется правильный многоугольник с 4 сторонами, с центром в начале координат плоскости. Это очень интересное свойство, которое мы подробно рассмотрим позже (в разделе примеров).
Теперь, когда мы разъяснили это понятие, мы увидим, как вычислить корень комплексного числа в полярной форме (использование таких обозначений наиболее удобно для решения корня.). Проще говоря, вам нужно вычислить корень модуля и выразить аргумент через n. Другими словами, корень следующего комплексного числа (z):
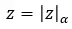
Эти суммы для расчета:
- Модуль: корень n-й степени исходного модуля.
- Аргумент: прибавьте к аргументу 2πk в радианах или 360k в градусах и разделите на n.
Математически для расчета модуля и аргумента мы используем следующие две формулы:
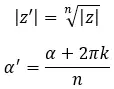
Где k = 0, 1, 2, …, n-1.
И, следовательно, выразим результат следующим образом:
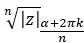
Чтобы внести ясность, n решений, которые мы получим в результате решения этого корня, будут сформированы одним и тем же модулем и n разными аргументами.
Примеры вычисления корней комплексов n-й степени
Теперь мы увидим несколько примеров по вычислению корней n-й степени из комплексных чисел. Мы рекомендуем вам попытаться решить их самостоятельно, а когда вы закончите, посмотрите исправление. Не забывайте, что метод описан чуть выше.
Найдите третий корень комплексного числа: 1 + i √3 .
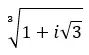
Найдите корень четвертой степени комплексного числа: 3+i √ 3 .
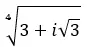
Узнайте о корнях комплексных чисел
- Комплексные числа
- Операции над комплексными числами
- сложные полномочия
- Свойства комплексных чисел