На этой странице мы объясняем, что такое квадратная матрица, и вы найдете примеры квадратных матриц. Кроме того, вы увидите, какими свойствами обладают квадратные матрицы, какие операции с ними можно производить и какие существуют различные типы.
Что такое квадратная матрица?
Квадратная матрица – это матрица, имеющая такое же количество строк, что и столбцов.
Примеры квадратных матриц
квадратная матрица второго порядка
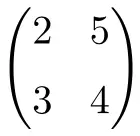
квадратная матрица третьего порядка
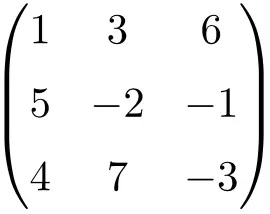
квадратная матрица 4-го порядка
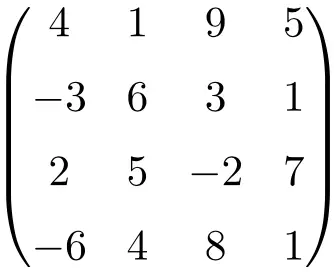
Как видите, квадратные матрицы обычно называются по их порядку, т.е. квадратная матрица порядка 2 означает, что это матрица размерности 2×2 (2 строки и 2 столбца), или мы говорим о квадратной матрице порядка 3. что указывает на то, что он имеет размер 3×3 (3 строки и 3 столбца).
Диагонали квадратной матрицы
Диагонали квадратных матриц имеют особые названия, есть главная диагональ и второстепенная диагональ:
- Основная диагональ квадратной матрицы состоит из элементов, идущих из левого верхнего угла в правый нижний угол:

- Вторичная диагональ квадратной матрицы соответствует элементам, идущим из левого нижнего угла в правый верхний угол:

Свойства квадратной матрицы
Квадратные матрицы широко используются в линейной алгебре, поэтому они так важны. Итак, давайте посмотрим, какие характеристики делают этот класс матриц настолько актуальным:
- Любую квадратную матрицу можно разложить в сумму симметричной и антисимметричной матриц .
- Если две квадратные матрицы одного порядка, их можно складывать или вычитать друг из друга:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- Две квадратные матрицы можно умножать в обоих возможных направлениях. Однако произведение квадратных матриц не является коммутативным, то есть результат умножения будет меняться в зависимости от того, на какую сторону оно умножается. Обратите внимание в следующем примере, как результат зависит от положения матриц:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Квадратные матрицы — единственные, которые могут вычислить определитель. Следовательно, определитель может быть решен только в том случае, если он является квадратной матрицей. Например, чтобы найти определитель квадратной матрицы 3×3, необходимо применить правило Сарруса:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Также помните, что если определитель матрицы отличен от 0, это означает, что это правильная матрица , то есть она обратима. С другой стороны, если определитель равен нулю, это сингулярная матрица (которая не имеет обратной).
- Наконец, квадратные матрицы можно диагонализировать . Таким образом, смену базы можно провести для вычисления собственных значений (или собственных значений) и собственных векторов (или собственных векторов) квадратной матрицы.
Операции с квадратными матрицами
Как мы видели, определитель матрицы можно вычислить только в том случае, если матрица квадратная. Аналогично, существуют определенные операции, которые можно выполнить только в том случае, если матрица имеет квадратную размерность:
след матрицы
След матрицы — это сумма элементов, образующих главную диагональ квадратной матрицы.
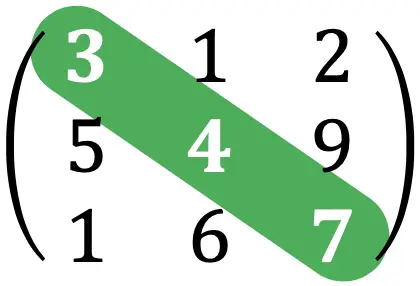
Например, трассировка матрицы из приведенного выше упражнения будет такой:
![]()
Виды квадратных штампов
Тогда у вас есть наиболее важные типы существующих квадратных матриц. Нажмите на тип кубика, чтобы узнать, что в нем особенного.

Треугольная матрица

диагональная матрица

Матричная идентичность

Симметричная матрица
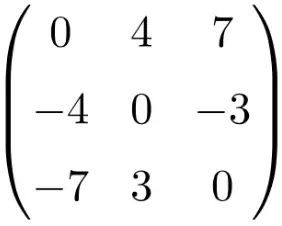
Антисимметричная матрица
Как видите, существует множество типов квадратных матриц, и каждая по разным причинам имеет свое название.