На этой странице вы найдете формулу квадрата суммы, то есть примечательное тождество (a+b) 2 . Вы также сможете увидеть примеры и решенные упражнения на суммы в квадрате. И более того, вы откроете для себя геометрические свойства, скрытые в этом замечательном изделии.
Чему равен квадрат суммы?
Квадрат суммы — одно из примечательных тождеств (или примечательных произведений), поэтому это математическое правило, позволяющее быстро вычислить степень бинома с двумя возведенными в квадрат положительными членами.
Таким образом, квадрат суммы состоит из двух разных слагаемых, сложенных вместе и возведенных в квадрат, то есть алгебраическое выражение квадрата суммы равно (a+b) 2 .
Формула квадрата суммы
Учитывая математическое определение этого замечательного типа тождества, мы теперь увидим, какова формула квадрата суммы :

Так что квадрат суммы равен квадрату первого члена плюс удвоенное произведение первого на второе плюс квадрат второго.
Таким образом, чтобы решить квадрат суммы, недостаточно возвести каждое сложение в два, но, кроме того, два сложения необходимо умножить вместе и на 2.
Это важно помнить, поскольку очень распространенной ошибкой при сложении квадратов является забывание произведения между двумя членами и вычисление только квадратов:

Помните, что нельзя исключать какие-либо члены из формулы!
С другой стороны, помните, что формула квадрата вычитания (или квадрата вычитания) очень похожа на ту, которую мы только что видели, но в ней есть отличие, которое полностью меняет результат. Если вы не уверены, как это выглядит, вы можете узнать здесь, что такое формула вычитания в квадрате и как она применяется.
Примеры сумм квадратов
Вот несколько практических примеров, чтобы вы могли понять, как возводить сумму в квадрат:
Пример 1
- Вычислите следующую сумму в квадрате, применив формулу:
![]()
Формула квадрата суммы:
![]()
Сначала нам необходимо определить параметры
![]()
И
![]()
формулы. В этом случае,
![]()
представляет собой
![]()
пары и
![]()
соответствуют номеру 5:
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Ну, поскольку теперь мы знаем значения
![]()
и из
![]()
Мы можем применить формулу, чтобы найти результат квадрата суммы:

Пример 2
- Решите следующее выражение для квадрата суммы:
![]()
Формула квадрата суммы:
![]()
Итак, в этой задаче
![]()
это моном
![]()
И с другой стороны,
![]()
является независимым членом 4:
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
Наконец, как только мы определили значения
![]()
и из
![]()
, мы применяем формулу суммы в квадрате для решения примечательного произведения:
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
Доказательство формулы квадрата суммы
Затем мы выведем только что увиденную формулу из квадрата суммы, чтобы вы поняли, откуда она берется.
Начиная с положительного бинома, повышенного до 2:
![]()
Приведенная выше степень, очевидно, эквивалентна множителю
![]()
умноженное само на себя:
![]()
Итак, умножаем две скобки, используя распределительное свойство:
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Наконец, из полученных слагаемых группируем схожие:
![]()
И мы уже пришли к полиномиальному выражению формулы, значит, она доказана:
![]()
Хотя в это может быть трудно поверить, квадрат формулы суммы также работает для факторизации квадратичных многочленов . Если вы не знаете, что это такое, разложение полинома — это процедура, часто используемая в математике для упрощения выражения многочлена. Узнайте, как это сделать, перейдя по ссылке выше.
Геометрическая интерпретация квадрата суммы
До сих пор мы видели, как математически вычисляется квадрат суммы, но это замечательное произведение можно интерпретировать и геометрически.
Посмотрите на следующий квадрат, стороны которого равны
![]()
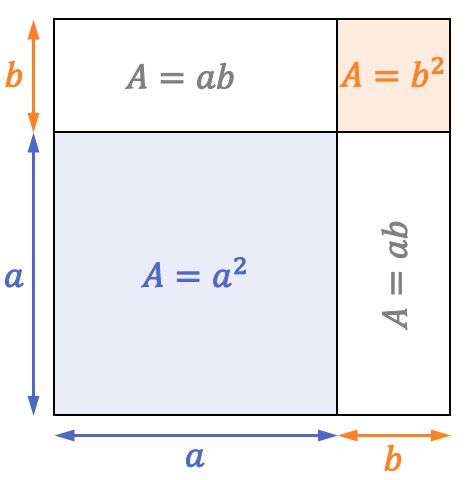
Площадь квадрата равна длине одной из его сторон в квадрате. Следовательно, поскольку сторона предыдущего квадрата равна
![]()
его площадь (или поверхность) равна
![]()
Ну, как вы можете видеть на квадратном изображении, квадрат площадью
![]()
прямоугольники с двумя областями
![]()
и еще один квадрат поверхности
![]()
Следовательно, формула суммы квадрата выполняется и с геометрической точки зрения:
![]()
Решенные задачи о квадрате суммы
Затем мы оставляем вам несколько пошаговых упражнений на решение сумм квадратов, чтобы вы могли попрактиковаться и, таким образом, завершить понимание концепции. Все свои вопросы вы можете написать нам в комментариях, и мы с радостью на них ответим. 💭💭💭
Упражнение 1
Определите следующие суммы в квадрате:
![]()
![]()
![]()
![]()
Для решения всех заметных тождеств задачи достаточно применить формулу квадрата суммы:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Упражнение 2
Решите следующие квадраты суммы двух членов, применив формулу:
![]()
![]()
![]()
Чтобы вычислить все значимые продукты задачи, необходимо использовать формулу квадрата суммы:
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
В разделе Б) нужно помнить, что если корень возведен в квадрат, то он упрощается:
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
Мономы последней суммы, возведенной в квадрат, имеют дробные коэффициенты, поэтому для ее решения также необходимо использовать свойства дробей:
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Упражнение 3
Найдите следующую степень, применив формулу квадрата суммы и не используя калькулятор:
![]()
Прежде всего, число семнадцать можно разложить на сумму 10 плюс 7:
![]()
Итак, мы преобразовали степень в квадрат суммы. Поэтому теперь мы можем применить соответствующую формулу:
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
Короче говоря, результат потенцирования таков:
![]()
Как вы видели в этом упражнении, формула суммы квадратов также полезна для вычисления степеней больших чисел без использования калькулятора.
Квадрат суммы трех слагаемых
Иногда мы можем обнаружить, что нам нужно решить квадрат трех добавленных членов, т.е. (a+b+c) 2 . По логике вещей, в этих случаях мы не можем использовать объясненную нами формулу, потому что внутри круглых скобок вместо бинома стоит трехчлен. Поэтому необходимо использовать другую формулу.
Формула квадрата суммы трех слагаемых выглядит следующим образом:
![]()
Давайте посмотрим, как эта формула применяется на примере:
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
Как видите, добавление в формулу одного элемента значительно усложняет результат.