Квадрат разности (или вычитания)

Здесь мы объясняем, что такое примечательная формула тождества квадрата разности (или вычитания), то есть мы покажем вам, как решается выражение (ab) ² . Кроме того, вы сможете увидеть примеры и потренироваться на упражнениях, решенных на квадрате разности. И, наконец, мы покажем демонстрацию формулы и геометрическую интерпретацию этого замечательного типа продукта.

Чему равен квадрат разности (или вычитания)?

Квадрат разности , или квадрат вычитания , является одним из примечательных тождеств (или примечательных произведений), то есть состоит из математического правила, облегчающего вычисление квадратуры «бинома с двумя членами: одним положительным и другой отрицательный.

Следовательно, алгебраическое выражение квадрата разности равно (ab) ² .

Формула квадрата разности (или вычитания)

Увидев определение этого типа замечательного тождества, мы увидим, как решить квадрат разности с помощью его формулы:

Так что квадрат разности равен квадрату первого слагаемого минус удвоенное произведение первого на второе плюс квадрат второго.

Итак, чтобы вычислить разность или вычитание в квадрате, необходимо не только возвести каждое слагаемое до двух, но и умножить их вместе и на 2.

Это важно помнить, потому что очень распространенная ошибка при вычитании квадратов заключается в том, что не помещают произведение между двумя членами, а решают только квадрат уменьшения и вычитание вычитания:

Не забудьте произведение между a и b!

Примеры квадратов разности (или вычитания)

Теперь, когда мы знаем формулу квадрата разности, мы можем производить с ее помощью расчеты. И чтобы вы могли увидеть, как это делается, мы подготовили несколько примеров решения квадрата разности (или вычитания).

Пример 1

Решите следующую разность в квадрате:

$(x-3)^2$

Это вычитание в квадрате, поэтому вам придется применить его формулу:

$(a-b)^2=a^2-2ab+b^2$

Итак, мы должны определить, каковы значения неизвестных

$a$

$b$

формулы. В этом случае,

$a$

это переменная

$x$

$b$

соответствуют номеру 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Обратите внимание, что отрицательный знак не является частью

$b,$

но для правильного применения формулы всегда нужно брать число без знака.

Таким образом, мы уже знаем значения

$a$

и из

$b$

Поэтому нам нужно только подставить эти значения в формулу:

бином квадрата упражнения на вычитание решены

Пример 2

Вычислите следующий бином квадрата вычитания:

$(5x-2)^2$

Формула квадрата разности:

$(a-b)^2=a^2-2ab+b^2$

Итак, сначала нам необходимо определить значения

$a$

и из

$b$

формулы. В этой проблеме

$a$

представляет собой моном

$5x$

$b$

эквивалентно независимому члену бинома, т.е. 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

Наконец, как только мы узнаем значения параметров

$a$

$b$

, мы просто применяем биномиальную формулу для вычитания в квадрате:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

Доказательство формулы квадрата разности

Затем мы выясним, откуда взялась формула квадрата вычитания. Хотя вам не обязательно запоминать доказательство, все равно приятно понять лежащую в его основе математику.

Если мы начнем с выражения бинома всех вычитаний:

$(a-b)^2$

Очевидно, предыдущая степень равна произведению множителя

$(a-b)$

умноженное само на себя:

$(a-b)^2= (a-b)\cdot (a-b)$

Теперь умножим две скобки, применив распределительное свойство:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

И нам просто нужно сгруппировать похожие члены вместе, чтобы закончить доказательство формулы:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Чтобы формула квадрата вычитания была математически доказана:

$(a-b)^2=a^2-2ab+b^2$

Любопытно, что разложение биномиального выражения вычитания в квадрате также известно как идеальный квадратный трехчлен.

Геометрическая интерпретация квадрата разности

Чтобы завершить понимание понятия квадрата разности, мы увидим, как геометрически интерпретировать это замечательное равенство.

Посмотрите на следующий квадрат со сторонами длиной

$a:$

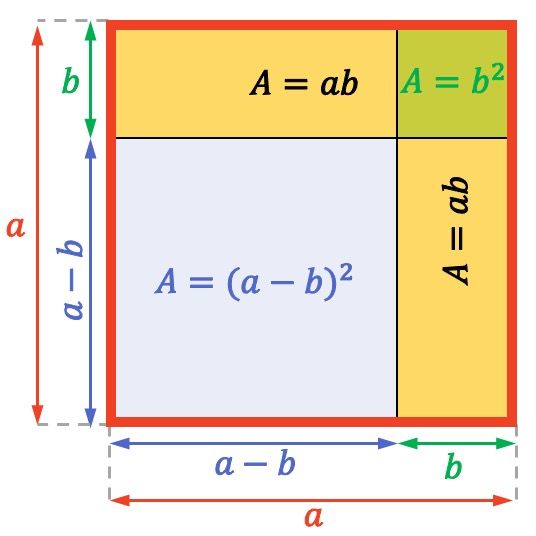
геометрическая интерпретация квадрата разности

Площадь (или площадь поверхности) квадрата или прямоугольника вычисляется путем умножения двух соседних сторон. Следовательно, площадь всего целочисленного квадрата выше равна

$a\cdot a = a^2.$

Аналогично площадь каждого желтого прямоугольника равна

$a\cdot b = ab.$

И, наконец, маленький квадрат, показанный вверху справа, имеет площадь

$b\cdot b =b^2.$

Это означает, что квадрат со стороной

$(a-b),$

поверхность которого

$(a-b)^2,$

можно разложить на площадь квадрата размером

$a,$

минус 2 раза площадь прямоугольника размеров

$a$

$b$

, плюс площадь бокового квадрата

$b.$

Короче говоря, формулу квадрата разности можно проверить и геометрически:

$(a-b)^2=a^2-2ab+b^2$

Решенные задачи о квадрате разности (или вычитания)

Чтобы вы могли попрактиковаться, мы оставляем вам несколько упражнений, решаемых шаг за шагом на заметное произведение квадрата разности. Помните, что вы можете написать нам любые вопросы, которые у вас есть ниже в комментариях.

Упражнение 1

Решите следующие вычитания в квадрате:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

посмотреть решение

Чтобы найти все замечательные тождества задачи, достаточно применить формулу квадрата разности, которая имеет вид:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

Упражнение 2

Определите следующие квадраты разностей двух величин, применив формулу:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

посмотреть решение

Для определения всех значимых произведений задачи необходимо воспользоваться формулой вычитания в квадрате:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

Для решения раздела Б) нужно помнить, что если корень возведен в квадрат, то он упрощается:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

Мономы последнего квадрата вычитания имеют дробные коэффициенты, поэтому для его решения нужно использовать свойства дробей:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

Чему равен квадрат разности (или вычитания)?

Формула квадрата разности (или вычитания)

Примеры квадратов разности (или вычитания)

Пример 1

Пример 2

Доказательство формулы квадрата разности

Геометрическая интерпретация квадрата разности

Решенные задачи о квадрате разности (или вычитания)

Упражнение 1

Упражнение 2

Оставьте комментарий Отменить ответ