На этой странице мы объясняем, что такое система координат, и, кроме того, вы найдете все о декартовой системе координат. Вы также увидите другие типы систем координат (полярные, цилиндрические, сферические и т. д.) и реальные применения систем координат.
Что такое система координат?
Хотя на первый взгляд эту концепцию немного сложно понять, определение системы координат следующее:
Система координат — это система, которая позволяет нам определять положение точки. То есть это набор значений, используемый для определения местоположения любого геометрического объекта.
Например, положение, в котором летит следующий самолет, можно описать системой координат:
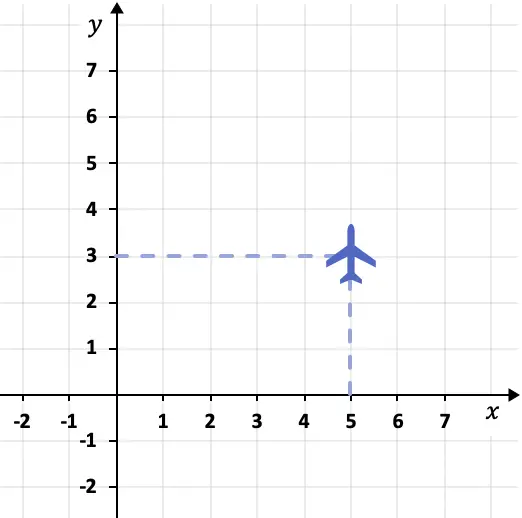
В этом случае плоскость находится в точке (5.3). Потому что его координата X равна 5, а координата Y равна 3.
![]()
С другой стороны, точка (0,0) называется началом координат , поскольку именно здесь начинаются оси координат и она является опорной точкой системы координат.
Из любопытства считается, что математиком, придумавшим систему координат, был француз Рене Декарт. Именно поэтому ее еще называют декартовой системой координат.
Декартова система координат на плоскости
График, который мы видели в предыдущем разделе, принадлежит декартовой системе координат на плоскости. Мы говорим, что он находится в плоскости, потому что это двумерная система, то есть у нее есть только две оси: ось X и ось Y.
Ось X соответствует горизонтальным координатам, а ось Y представляет вертикальные координаты. Ниже вы можете увидеть несколько точек, представленных графически с их координатами:
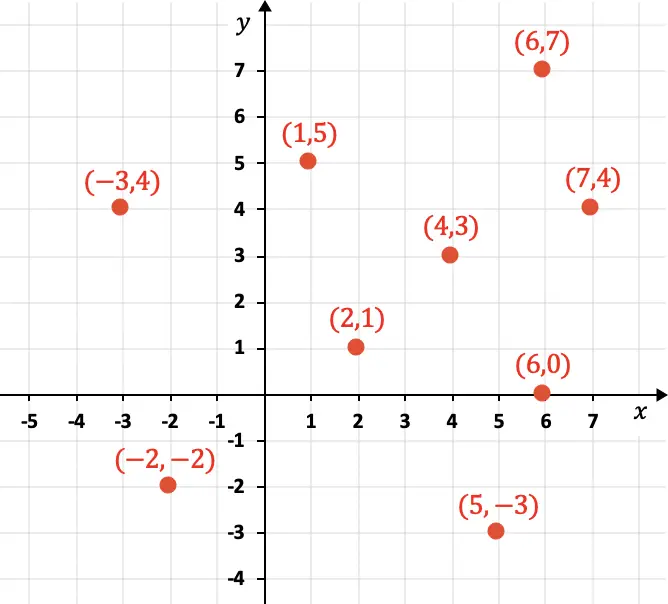
Как видно на графике, координаты представлены численно в круглых скобках, кроме того, сначала ставится компонент X, а затем компонент Y: (4,3). Кроме того, координаты могут быть положительными, отрицательными или нулевыми.
С другой стороны, этот тип системы координат также называют декартовой плоскостью.
Наконец, вы должны знать, что оси координат можно обозначить по-разному, хотя все они означают одно и то же:
- Ось X также называется осью абсцисс или осью OX.
- Ось Y также называется осью y или осью OY.
Декартова система координат в пространстве
Мы только что увидели, как представить точку на плоскости, то есть в системе координат с двумя осями (2 измерения). Однако реальность состоит из трех измерений (высота, ширина и глубина).
Таким образом, в евклидовой геометрии трехмерное пространство обычно представляется системой координат с тремя осями, перпендикулярными друг другу:
- Ось X представляет глубину.
- Ось Y указывает ширину.
- Ось Z соответствует высоте.
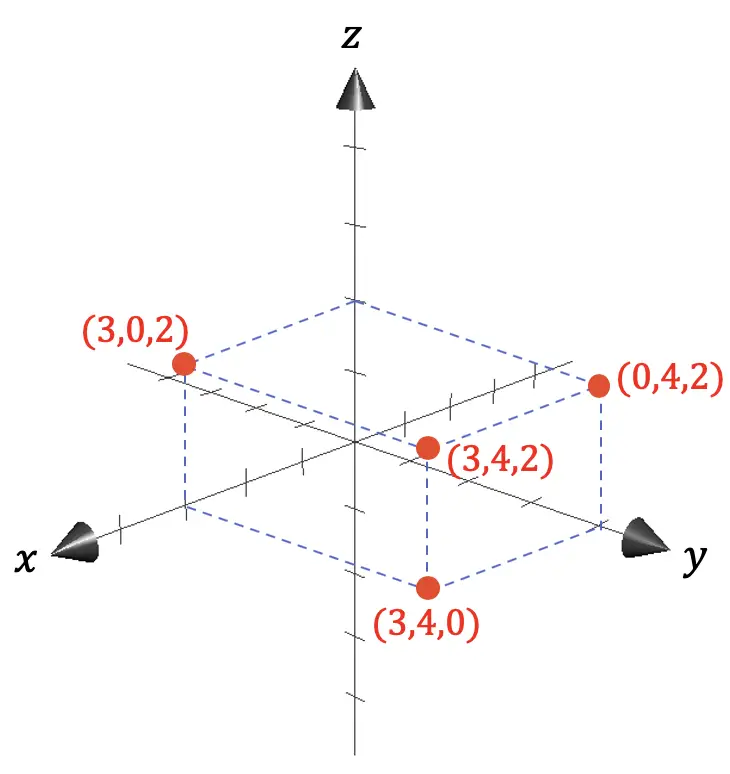
Как видно из предыдущего графического представления, координаты любой точки задаются проекциями на оси расстояний между рассматриваемой точкой и началом координат (0,0,0).
полярная система координат
Наиболее широко используются декартовы системы координат, 2D или 3D. Но в некоторых случаях нам может быть удобно использовать другой тип системы координат.
Полярная система координат — это двумерная система отсчета, координаты которой:
-

— расстояние между началом координат и точкой. Это называется радиальной координатой.
-

— это угол, который ось X образует с линией, проходящей через точку и начало координат. Это называется угловой или азимутальной координатой.
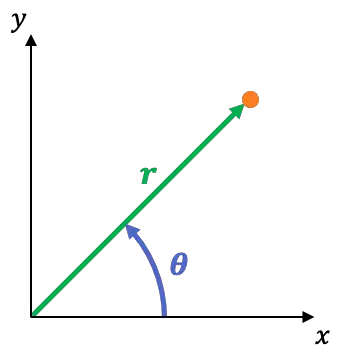
Вы можете легко переключиться с прямоугольной системы координат на полярную систему координат, используя следующие уравнения:
Преобразование полярных координат в декартовы координаты
![]()
![]()
Переход от декартовых координат к полярным координатам
![]()
![]()
Цилиндрическая система координат
Цилиндрическая система координат очень похожа на полярную систему координат. По сути, это то же самое, но с еще одной координатой: высотой.
Таким образом, цилиндрическая рамка является трехмерной, то есть с тремя координатами:
-

— это ортогональная проекция точки на плоскость XY или, другими словами, расстояние точки от оси Z.
-

— угол, под которым положительная полуось

-

— высота точки, — та же координата декартовой системы координат в пространстве.
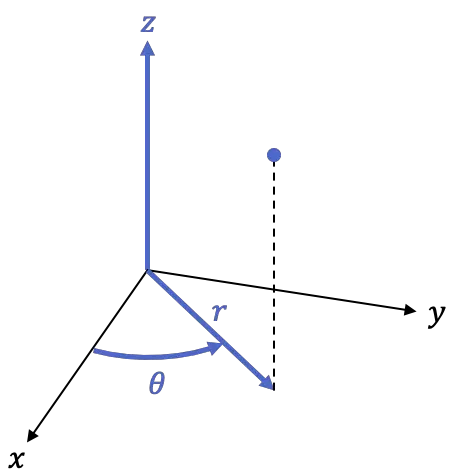
Следующие формулы используются для преобразования декартовой системы координат в цилиндрические координаты:
Преобразование цилиндрических координат в декартовы координаты
![]()
![]()
![]()
Преобразование декартовых координат в цилиндрические координаты
![]()
![]()
![]()
Сферическая система координат
Наконец, у нас есть сферическая система координат. Этот тип системы координат также весьма похож на полярные координаты и цилиндрические координаты, хотя, очевидно, имеет от них некоторые отличия.
Сферическая система координат является системой описания трехмерных евклидовых пространств, поэтому имеет три координаты:
-

— расстояние (в R3) от начала координат до точки.
-

— это угол, который положительная часть оси X составляет с линией

проецируется в плоскость XY.
-
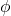
— угол между положительной частью оси Z и линией

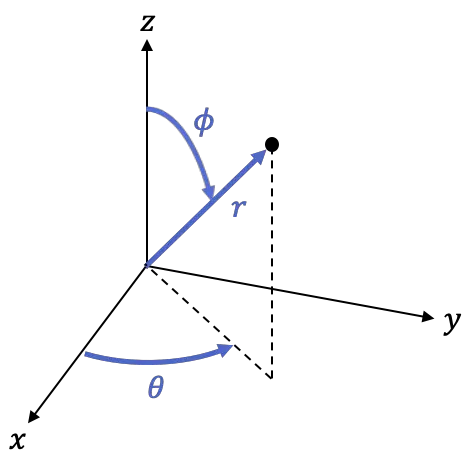
Вы можете переключаться между сферическими и декартовыми координатами, используя следующие формулы:
Преобразование сферических координат в декартовы координаты
![]()
![]()
![]()
Преобразование декартовых координат в сферические координаты
![]()
![]()
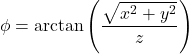
Реальные применения системы координат
Системы координат так важны в математике, потому что они также используются в реальной жизни. Например, они полезны для определения местоположения объектов, людей или даже мест на карте. Фактически, GPS существует благодаря системам координат, поскольку именно с их помощью можно узнать ваше положение на Земле.
Точнее, географические координаты GPS состоят из двух элементов: широты и долготы. Широта (север или юг) и долгота (восток или запад) — это две угловые координаты, которые измеряют угол между центром Земли и вашим местоположением. Оба выражаются в градусах, в десятичных или шестидесятеричных координатах.