Здесь вы найдете все о функции гиперболического косинуса: какова ее формула, ее графическое представление, ее характеристики, математические связи с другими функциями и т. д.
Формула гиперболического косинуса
Функция гиперболического косинуса является одной из основных гиперболических функций и обозначается символом cosh(x) . Гиперболический косинус равен сумме e x плюс e -x , разделенной на 2.
Следовательно, формула гиперболического косинуса имеет вид:
![]()
Таким образом, гиперболический косинус математически связан с показательной функцией. По следующей ссылке вы можете увидеть свойства этого типа функции:
➤ См.: свойства показательной функции.
Графическое изображение гиперболического косинуса
Графическое представление функции гиперболического косинуса имеет форму квадратичной функции (или параболы):

➤ См.: Графическое представление квадратичной функции .
На этом графике мы ясно видим, что гиперболический косинус является четной функцией, поскольку он симметричен относительно оси Y.
С другой стороны, график гиперболического косинуса сильно отличается от графика косинуса (тригонометрической функции), который является периодической функцией. Графическое представление косинуса и все различия с гиперболическим косинусом вы можете увидеть по следующей ссылке:
➤ См.: графическое представление функции косинуса.
Характеристики гиперболического косинуса
Гиперболический косинус обладает следующими свойствами:
- Областью определения функции гиперболического косинуса являются все действительные числа:
![]()
- Вместо этого диапазон (или диапазон) функции гиперболического косинуса равен 1 и все числа больше 1:
![]()
- Гиперболический косинус — непрерывная и четная функция.
![]()
- Функция пересекает ось Y в точке x=0.
![]()
- С другой стороны, функция не имеет точки пересечения с осью X.
- Два предела бесконечности (положительный и отрицательный) гиперболической функции косинуса дают плюс бесконечность.
![]()
![]()
- Гиперболический косинус уменьшается до тех пор, пока x = 0, а затем бесконечно увеличивается, поэтому функция имеет минимум при x = 0.
![]()
- Функция выпукла во всей своей области определения, поэтому у нее нет точки перегиба.
- Производной функции гиперболического косинуса является гиперболический синус:
![]()
- Интеграл от функции гиперболического косинуса представляет собой гиперболический синус:
![]()
- Полином Тейлора (или ряд Маклорена) гиперболической функции косинуса выглядит следующим образом:
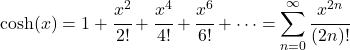
- Преобразование Лапласа функции гиперболического косинуса выглядит следующим образом:
![]()
Математические соотношения гиперболического косинуса
Далее мы увидим, как гиперболический косинус можно вычислить из других гиперболических функций, поскольку все они математически связаны.
Фундаментальное уравнение связывает гиперболический косинус с гиперболическим синусом:
![]()
➤ См.: гиперболический синус.
Три основные гиперболические функции (гиперболический синус, косинус и тангенс) могут быть связаны следующим уравнением:
![]()
С другой стороны, гиперболический косинус сложения (или вычитания) двух разных чисел можно определить по следующим формулам:
![]()
![]()
Гиперболический косинус удвоенного числа равен сумме квадратов гиперболического косинуса и гиперболического синуса этого числа:
![]()
Сложение или вычитание двух гиперболических косинусов можно рассчитать, применяя следующие формулы:
![]()
![]()
Наконец, квадрат гиперболического косинуса можно вычислить по следующей формуле:
![]()