Здесь вы узнаете, что такое вертикальные асимптоты функции (с примерами). Мы также объясним, как найти вертикальные асимптоты функции, и, кроме того, вы сможете попрактиковаться в упражнениях, решаемых шаг за шагом.
Что такое вертикальная асимптота?
Вертикальная асимптота функции — это вертикальная линия, график которой неограниченно приближается, ни разу не пересекая ее. Следовательно, уравнение вертикальной асимптоты имеет вид x=k , где k — значение вертикальной асимптоты.
То есть k является вертикальной асимптотой, если предел функции при приближении x к k бесконечен.
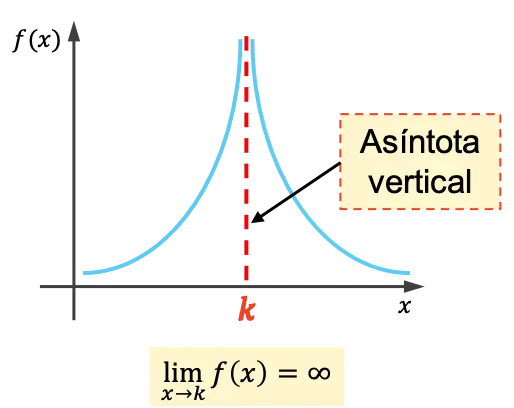
Как вычислить вертикальную асимптоту функции
Чтобы вычислить вертикальную асимптоту функции, необходимо выполнить следующие шаги:
- Найдите область определения функции. Если все точки находятся в области определения, функция не имеет вертикальных асимптот.
- Вычислите предел функции в точках, не входящих в область определения.
- Вертикальными асимптотами функции будут все значения, при которых предел дает бесконечность.
Обратите внимание, что функция может иметь более одной вертикальной асимптоты. Например, график касательной функции имеет бесконечное количество вертикальных асимптот.
➤ См.: характеристики функции тангенса.
Пример вертикальной асимптоты
В качестве примера мы найдем все асимптоты следующей рациональной функции, чтобы вы могли увидеть, как это делается:
![]()
В общем случае точки, в которых существуют вертикальные асимптоты, не принадлежат области определения функции. Поэтому сначала вычислим область определения функции.
Это рациональная функция, поэтому мы смотрим на то, когда знаменатель обращается в нуль, чтобы определить точки, которые не принадлежат области определения:
![]()
![]()
Следовательно, областью определения функции являются все действительные числа, кроме x=2:
![]()
Таким образом , x=2 может быть вертикальной асимптотой функции. Чтобы убедиться в этом, мы должны вычислить предел функции в этой точке:
![]()
В этом случае мы получили неопределенность числа между нулем и, следовательно, для решения предела мы должны вычислить боковые пределы, чтобы узнать, равно ли оно плюс бесконечности, минус бесконечности или предел не существует. Однако, когда мы вычисляем вертикальные асимптоты, нам не нужно делать боковые пределы, но получения этой неопределенности достаточно, чтобы сказать, что это вертикальная асимптота.
Короче говоря, поскольку предел функции при приближении x к 2 дает бесконечность, x=2 является вертикальной асимптотой.
Ниже функция представлена графически. Как видите, она очень близко подходит к линии x=2 (как слева, так и справа), но никогда не пересекает ее, поскольку является вертикальной асимптотой:

Кроме того, по графику можно вывести боковые пределы функции в точке x=2:
![]()
Решенные задачи о вертикальных асимптотах
Упражнение 1
Вычислите вертикальную асимптоту следующей рациональной функции:
![]()
Не существует формулы для расчета вертикальных асимптот функции, но вам нужно найти область определения функции и посмотреть, в каких точках, где функция не определена, предел дает бесконечность.
Поэтому положим знаменатель рациональной функции равным 0, чтобы найти точки, не принадлежащие области определения:
![]()
![]()
![]()
Таким образом, областью определения функции являются все действительные числа, кроме x=1/2:
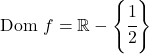
Таким образом, x=1/2 может быть вертикальной асимптотой. Чтобы это проверить, вычислим предел функции в этой точке:
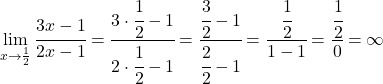
Итак , x=1/2 является вертикальной асимптотой , поскольку предел функции в этой точке дает бесконечность.
Упражнение 2
Найдите все вертикальные асимптоты следующей дробной функции:
![]()
Сначала устанавливаем знаменатель дроби равным нулю, чтобы увидеть, какие значения не входят в область определения функции:
![]()
Решаем неполное квадратное уравнение:
![]()
![]()
Таким образом, областью определения рациональной функции является:
![]()
Итак, чтобы определить, какое из этих двух значений является вертикальными асимптотами, мы находим предел функции в каждой точке:
![]()
![]()
Два предела дают бесконечность, поэтому x=3 и x=-3 — две вертикальные асимптоты проблемной функции .
Упражнение 3
Найдите, если они у вас есть, все вертикальные асимптоты следующей рациональной функции:
![]()
➤ См.: неопределенность ноль между нулем.
Сначала решаем квадратное уравнение знаменателя, чтобы найти значения, сокращающие знаменатель дроби:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Итак, область определения функции:
![]()
Итак, сначала вычисляем предел функции при x=1:
![]()
И, с другой стороны, мы решаем предел функции, когда x стремится к -3:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
Предыдущий предел дает неопределенную форму от нуля до нуля, поэтому для его решения нам нужно факторизовать полиномы. Если у вас есть какие-либо сомнения относительно того, как мы решили предел, вы можете увидеть полное объяснение того, как решить этот тип неопределенности, по ссылке на оператор упражнения.
В этом случае только предел функции в точке x=1 дает бесконечность, поэтому x=1 — единственная вертикальная асимптота функции .