Антиэрмитова (или антиэрмитова) матрица

На этой странице вы увидите, что такое антиэрмитова матрица, также называемая антиэрмитовой матрицей. Вы найдете примеры антиэрмитовых матриц, все их свойства и форму этого типа комплексных квадратных матриц. Наконец, вы найдете объяснение того, как разложить любую комплексную матрицу на сумму антиэрмитовой матрицы и еще одной эрмитовой матрицы.

Что такое антиэрмитова или антиэрмитова матрица?

Антиэрмитова матрица , или также называемая антиэрмитовой матрицей, представляет собой квадратную матрицу с комплексными числами, сопряженное транспонирование которых равно той же матрице, но другого знака.

A^*=-A

Золото

A^*

— транспонированная сопряженная матрица

A

.

Из любопытства этот тип матрицы назван так потому, что он выполняет условие, противоположное эрмитовой матрице , имя которой происходит от имени выдающегося французского математика Шарля Эрмита, профессора и исследователя математики XIX века, который провел важные исследования, в том числе в область линейной алгебры.

Примеры антиэрмитовых матриц

После того, как мы увидели определение антиэрмитовой матрицы (или антиэрмитовой матрицы), мы увидим несколько примеров антиэрмитовых матриц разных размерностей:

Пример антиэрмитовой матрицы порядка 2×2

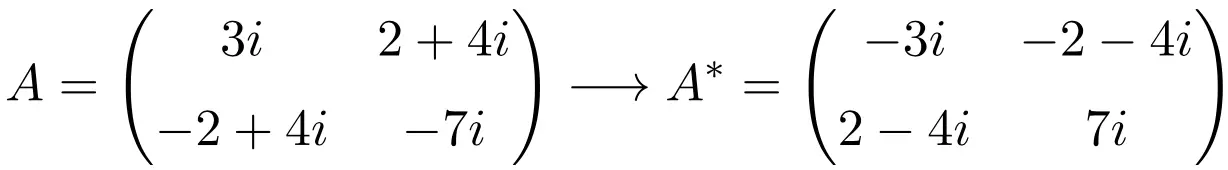
антиэрмитова или антиэрмитова матрица размерности 2x2

Пример антиэрмитовой матрицы размерности 3×3

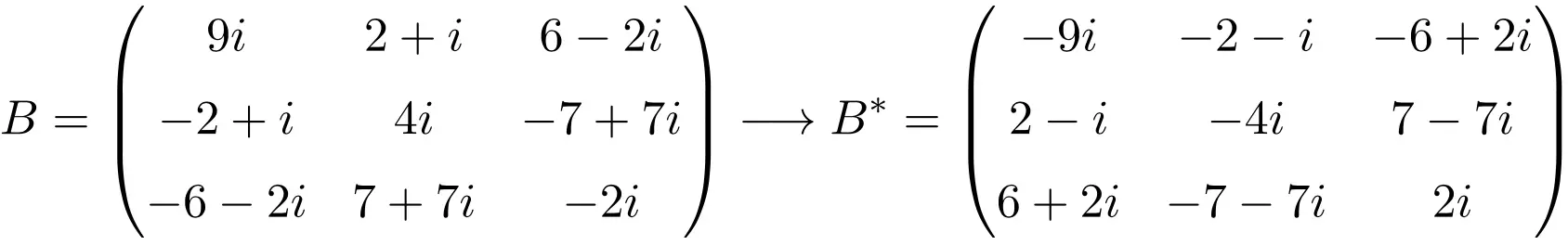
антиэрмитова или антиэрмитова матрица размерности 3x3

Пример антиэрмитовой матрицы размером 4×4

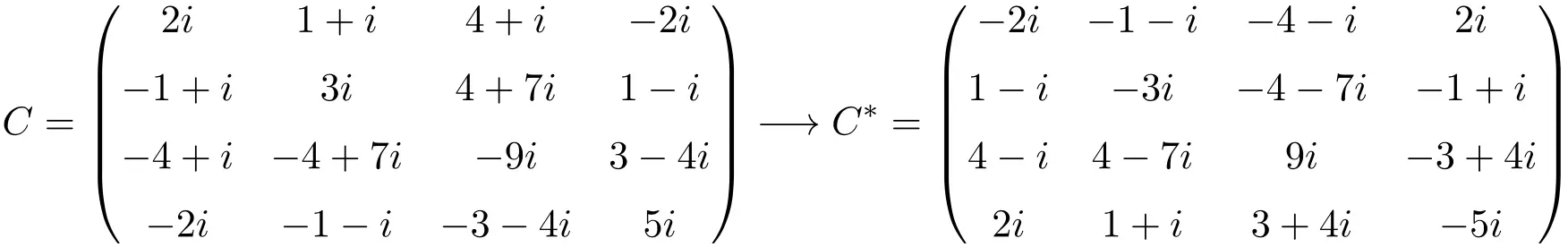
антиэрмитова или антиэрмитова матрица размерности 4x4

Как видите, матрицы A, B и C являются антиэрмитовыми, поскольку сопряженная транспонированная матрица каждой из них равна самой матрице, но со всеми элементами, изменившими знак.

Структура антиэрмитовой матрицы

Если вы уже рассмотрели предыдущие примеры, антиэрмитовы матрицы всегда имеют одинаковую структуру: они состоят из мнимых чисел (без вещественной части) на главной диагонали и комплексного элемента, расположенного на i-й строке и j-й линия. Столбец должен иметь ту же мнимую часть и ту же действительную часть, но с измененным знаком, что и элемент j-й строки и i-го столбца.

Хотя это может показаться немного сложным, лучше это понять на следующем примере:

Структура антиэрмитовой матрицы размерности 2×2

\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}

Как видим, элементы главной диагонали антиэрмитовой матрицы полностью мнимые, а элементы второстепенной диагонали имеют ту же мнимую часть, а действительная часть изменила знак.

Следовательно, действительная часть антиэрмитовой матрицы должна быть антисимметричной, а мнимая часть симметричной.

Свойства антиэрмитовой матрицы

Теперь мы увидим, каковы свойства этого типа квадратной комплексной матрицы:

  • Каждая антиэрмитова матрица является примером нормальной матрицы . Хотя не все нормальные матрицы являются антиэрмитными.
  • Любая антиэрмитова матрица диагонализуема. Более того, полученная диагональная матрица содержит только чисто мнимые элементы.
  • Следовательно, собственные значения (или собственные значения) антиэрмитовой матрицы всегда являются мнимыми числами.
  • Аналогично, собственные векторы (или собственные векторы) разных собственных значений антиэрмитовой матрицы ортогональны.
  • Матрица действительных чисел, то есть ни один элемент не имеет мнимой части, является антиэрмитовой тогда и только тогда, когда она является антисимметричной матрицей .
  • Антиэрмитова матрица может быть выражена как сумма действительной антисимметричной матрицы и мнимой симметричной матрицы .

A =B+Ci

  • Сумма (или вычитание) двух антиэрмитовых матриц равна другой антиэрмитовой матрице.
  • Результатом произведения антиэрмитовой матрицы и скаляра является другая антиэрмитова матрица, если скаляр является действительным числом.
  • Степень антиэрмитовой матрицы равна антиэрмитовой матрице, если показатель степени нечетный; с другой стороны, если ее возвести в четный показатель, результатом будет эрмитова матрица.
  • Ага

    A

    является антиэрмитовой матрицей, то произведение

    iA

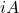
    является эрмитовой матрицей.

Разложение комплексной матрицы на антиэрмитову матрицу и эрмитову матрицу

Любую матрицу, содержащую комплексные числа, можно разложить на сумму антиэрмитовой матрицы плюс еще одну эрмитову матрицу . Но для этого необходимо знать следующие характеристики данных типов матриц:

  • Сумма квадратной комплексной матрицы плюс ее транспонированная сопряженная эквивалентна эрмитовой (или эрмитовой) матрице:

C + C^* = \text{Matriz Hermitiana}

  • Разница между квадратной комплексной матрицей и ее транспонированной сопряженной равна антиэрмитовой матрице:

C - C^* = \text{Matriz Antihermitiana}

  • Следовательно, все комплексные матрицы можно разложить в сумму эрмитовой и антиэрмитовой матриц. Эта теорема известна как разложение Теоплица :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Где C — комплексная матрица, которую мы хотим разложить, C* — ее транспонированная сопряженная матрица, и, наконец, A и B — соответственно эрмитова и антиэрмитова матрицы, на которые разлагается матрица C.

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх