Алгебраические дроби: упрощение, операции, решенные упражнения и т.д. -

На этой странице мы объясняем, что такое алгебраические дроби, когда они эквивалентны, как их упростить и как выполнять операции с алгебраическими дробями (сложение, вычитание, умножение и деление). Кроме того, вы сможете увидеть решенные пошаговые упражнения на алгебраические дроби. Короче говоря, здесь вы найдете все об алгебраических дробях.

Что такое алгебраические дроби?

В математике алгебраическая дробь — это дробь, у которой в числителе один полином, а в знаменателе — еще один полином.

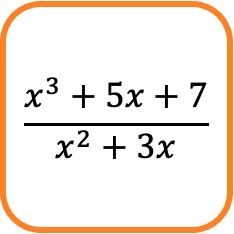
Например, приведенное выше дробное выражение представляет собой алгебраическую дробь, поскольку ее числитель и знаменатель состоят из многочленов.

Эквивалент алгебраической дроби

Зная определение алгебраических дробей, давайте посмотрим, когда две такие дроби равны.

Математически две алгебраические дроби эквивалентны , если выполняется следующее условие:

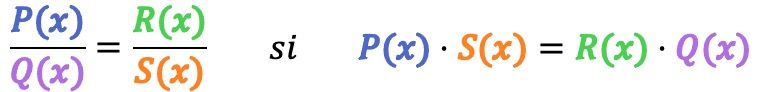
В качестве примера проверим, эквивалентны ли следующие 2 алгебраические дроби:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Чтобы определить, равны ли дроби алгебраически, умножим их члены поперечно:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Теперь посчитаем умножения многочленов:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Мы получили одно и то же выражение для обеих частей уравнения, поэтому фактически это две эквивалентные алгебраические дроби.

Упрощение алгебраических дробей

Чтобы упростить алгебраическую дробь, необходимо сначала разложить многочлены в числителе и знаменателе, а затем исключить общие для них множители.

Очевидно, что для упрощения алгебраических дробей важно знать , что такое полиномиальный факторинг и как он выполняется. Если вы все еще не знаете, как факторизуются многочлены, или не помните этого полностью, я рекомендую перейти на связанную страницу, прежде чем продолжить, иначе вы едва поймете эту процедуру. Он шаг за шагом объясняет, как факторизовать многочлены, и, кроме того, вы сможете увидеть несколько примеров и попрактиковаться в решенных упражнениях.

Теперь посмотрим, как упрощается алгебраическая дробь, применяя метод факторизации многочленов на примере:

Упростите следующую алгебраическую дробь:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Сначала факторизуем многочлены числителя и знаменателя дроби:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Если вы не знаете, как факторизовались многочлены, посмотрите ссылку выше)⬆

И как только мы факторизовали многочлены, мы устраняем общие делители между числителем и знаменателем, то есть удаляем все повторяющиеся члены:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

Таким образом, упрощенная алгебраическая дробь выглядит так:

$\cfrac{(x+1)(x+2)}{x-1}$

В этой задаче многочлены алгебраической дроби факторизовались путем нахождения их корней; однако иногда полином можно факторизовать напрямую, взяв общий множитель (гораздо более быстрый метод). По этой ссылке вы увидите, что значит взять общий множитель из многочлена, и узнаете , как упростить алгебраическую дробь, используя общий множитель.

Операции с алгебраическими дробями

Как и с любыми дробями, с алгебраическими дробями можно производить операции. В частности, алгебраические дроби можно складывать, вычитать, умножать и делить. Ниже мы шаг за шагом на примерах объясним, как рассчитывается каждый тип операции.

Сложение и вычитание алгебраических дробей

Процедура сложения и вычитания алгебраических дробей практически одинакова, поэтому разберем их вместе. Сначала мы увидим пример сложения двух алгебраических дробей, а ниже изучим разницу метода вычитания алгебраических дробей.

Сложение алгебраических дробей

Сложение алгебраических дробей производится так же, как и обычных дробей: сначала приводим дроби к общему знаменателю, а затем складываем числители.

Давайте посмотрим, как складывают алгебраические дроби на примере:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Сначала факторизуем знаменатели дробей:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Теперь нам нужно найти 1см (наименьшее общее кратное) знаменателей , чтобы привести дроби к общему знаменателю.

Совет: lcm знаменателей всегда формируется из произведения общих для них факторов, возведенных в наибольшую степень, умноженных на необщие множители .

Например, в нашем случае

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Общий делитель знаменателей, возведенных в наибольшую степень, равен

$(x+1)^2.$

А необщий множитель между знаменателями равен

$x.$

Следовательно, НЦМ знаменателей в данном случае составит:

$(x+1)^2 \cdot x$

Таким образом, lcm знаменателей равно

$(x+1)^2 \cdot x,$

следовательно, это будет новый знаменатель двух дробей.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Как только мы нашли общий знаменатель, мы должны изменить числители. Для этого проделаем тот же процесс, что и для сложения обычных дробей: для каждой дроби разделим жкм

$\bigl( \ x(x+1)^2 \ \bigr)$

между исходным знаменателем и умножить результат на числитель:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Итак, теперь мы можем сложить две дроби вместе, потому что у них одинаковый знаменатель:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Наконец, мы работаем с числителем. Сначала мы производим произведение монома и многочлена:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Далее добавляем аналогичные члены в числитель:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Обычно мы бы уже были там, но если мы внимательно посмотрим на эту проблему, мы сможем еще больше упростить алгебраическую дробь, удалив общий делитель из числителя. Еще:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

И вот мы уже завершили сумму двух алгебраических дробей.

Вычитание алгебраических дробей

Чтобы вычесть алгебраические дроби, мы должны выполнить процедуру, аналогичную сложению алгебраических дробей: сначала привести дроби к общему знаменателю, затем вычесть числители.

Давайте посмотрим, как вычитаются алгебраические дроби на примере:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Сначала нам нужно факторизовать знаменатели двух дробей:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Как и при вычитании обычных дробей, теперь нам нужно вычислить 1см (наименьшее общее кратное) знаменателей , чтобы привести дроби к общему знаменателю. В этом случае lcm знаменателей равно

$(x+2)^2(x-3) ,$

следовательно, это будет новый знаменатель двух дробей.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Теперь применим тот же процесс, что и для вычитания нормальных дробей: для каждой дроби делим lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

между исходным знаменателем и умножить результат на числитель:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Теперь соединим две алгебраические дроби, поскольку у них одинаковый знаменатель:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

И мы оперируем числителем. Сначала решаем полиномиальные умножения:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Очень распространенная ошибка при вычитании алгебраических дробей – забывание поставить круглые скобки после выполнения этого умножения. Это было бы ошибкой, поскольку отрицательный знак влияет на все результирующие элементы произведения, а не только на первый член.

Выполняем действия в скобках:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Таким образом, благодаря отрицательному знаку мы меняем знак всех слагаемых в скобках:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

И, наконец, группируем подобные одночлены:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Умножение алгебраических дробей

Для умножения алгебраических дробей сначала факторизуем все многочлены указанных дробей, затем умножаем между собой числители и знаменатели между собой и, наконец, упрощаем полученную дробь.

Поэтому произведение алгебраических дробей фактически вычисляется так же, как и произведение обычных дробей.

Далее посмотрим, как умножить две алгебраические дроби на примере:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Прежде всего вам нужно факторизовать все многочлены дробей, как числители, так и знаменатели:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Теперь перемножим дроби. Для этого перемножим числители и знаменатели между собой:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

И, наконец, упростим множители, которые повторяются в знаменателе и числителе:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Таким образом, результат умножения:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

Дробь не может быть упрощена дальше. Вот мы и закончили умножать алгебраические дроби.

Деление алгебраических дробей

Чтобы вычислить деление алгебраических дробей , мы сначала факторизуем все многочлены, затем умножаем дроби поперечно (первый числитель на второй знаменатель и первый знаменатель на второй числитель) и, наконец, упрощаем алгебраическую дробь.

Итак, давайте лучше разберемся, как делятся две алгебраические дроби, на примере:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

Первым шагом в делении двух алгебраических дробей является факторизация всех многочленов, участвующих в операции:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Теперь нам нужно разделить дроби. Для этого умножаем дроби поперечно, то есть первый числитель умножается на второй знаменатель и результатом будет числитель новой дроби, и точно так же первый знаменатель умножается на второй числитель. и результат будет знаменателем новой дроби:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Упростим множители, которые повторяются в знаменателе и числителе:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

И мы можем упростить дробь еще больше, поскольку

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

Дробь не может быть упрощена дальше. Поэтому мы уже разделили алгебраические дроби.

Решенные упражнения на алгебраические дроби

Ниже мы предлагаем вам несколько пошагово решенных упражнений по алгебраическим дробям, чтобы вы могли попрактиковаться и, таким образом, завершить понимание концепции. Не забывайте, что вы можете задать нам любые вопросы ниже в комментариях! 💬💬💬

Упражнение 1

Определите, эквивалентны ли следующие алгебраические дроби:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Посмотреть решение

Чтобы проверить, эквивалентны ли две алгебраические дроби, необходимо перемножить их поперечно и посмотреть, получится ли равенство. Итак, сначала проверим первую и вторую дробь:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Решим примечательное тождество в левой части уравнения:

$x^2-9=x^2-9$

✅

В данном случае мы получили равенство, поэтому первая и вторая дроби алгебраически равны.

Теперь применим ту же процедуру с первой и третьей алгебраической дробью:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Однако на этот раз алгебраические дроби не удовлетворяют уравнению, поэтому первая и третья дроби математически различны.

В заключение отметим, что третья дробь отличается от первой дроби и, следовательно, также не равна второй дроби, поскольку первая и вторая дроби эквивалентны.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Упражнение 2

Упростите следующие алгебраические дроби:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Посмотреть решение

Чтобы упростить алгебраическую дробь, нам нужно факторизовать многочлены в числителе и знаменателе, а затем исключить повторяющиеся множители. Еще:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Упражнение 3

Вычислите следующие сложения и вычитания алгебраических дробей:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Посмотреть решение

Чтобы сложить (или вычесть) алгебраические дроби, нужно сначала привести дроби к общему знаменателю, а затем сложить (или вычесть) числители. ТАК:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Упражнение 4

Решите следующие операции умножения и деления алгебраических дробей:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Посмотреть решение

Чтобы умножить алгебраические дроби, мы должны сначала факторизовать все многочлены, затем перемножить числители и знаменатели вместе и, наконец, упростить полученную дробь.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

С другой стороны, чтобы разделить алгебраические дроби, мы сначала факторизуем все многочлены, затем умножаем дроби поперечно (первый числитель на второй знаменатель и первый знаменатель на второй числитель) и, наконец, упрощаем найденную алгебраическую дробь.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Что вы думаете об объяснении? Тебе понравилось? Или у вас есть предложения? 💬 Расскажите нам, что вы думаете об этой странице в комментариях! Мы вас всех читаем! 👀 И не забывайте, что вы также можете задать нам все интересующие вас вопросы! ❔👇❔👇

Алгебраические дроби: упрощение, действия, решенные упражнения,…

Что такое алгебраические дроби?

Эквивалент алгебраической дроби

Упрощение алгебраических дробей

Операции с алгебраическими дробями

Сложение и вычитание алгебраических дробей

Сложение алгебраических дробей

Вычитание алгебраических дробей

Умножение алгебраических дробей

Деление алгебраических дробей

Решенные упражнения на алгебраические дроби

Упражнение 1

Упражнение 2

Упражнение 3

Упражнение 4

Оставьте комментарий Отменить ответ