▷ Всё об аналитической геометрии в пространстве ✅

На этой странице вы найдете объяснение всего, что касается аналитической геометрии в пространстве (и формул): уравнения прямой и плоскости, взаимное расположение плоскостей и линий, способы вычисления расстояний и углов в пространстве,…

Что такое геометрия в пространстве?

Геометрия пространства — раздел геометрии, отвечающий за изучение трёхмерных (3D) геометрических фигур, то есть тех, которые занимают определенное место в пространстве. Такие как конус, куб, пирамида, сфера, цилиндр, призмы, многогранники и т. д.

Однако на этой странице мы сосредоточимся на аналитической геометрии в пространстве , части космической геометрии, которая фокусируется на анализе точек, линий, плоскостей, расстояний между двумя геометрическими фигурами, угла, который они образуют, точек пересечения между различными геометрическими фигурами. цифры. элементы и т. д.

Уравнения линии в пространстве

Напомним, что математическое определение линии — это набор последовательных точек, представленных в одном направлении без кривых и углов.

Таким образом, для математического выражения любой линии в трехмерном пространстве (в R3) мы используем уравнения линии, и для их нахождения нам нужна только точка, принадлежащая линии, и вектор направления этой линии.

С помощью всего лишь этих двух геометрических элементов можно найти абсолютно все различные уравнения линии, а именно:

Уравнениями линии являются векторное уравнение , параметрические уравнения , непрерывное уравнение и неявное (или общее) уравнение .

Ниже вы найдете объяснение различных типов уравнений линии.

Векторное уравнение линии в пространстве

Ага

$\vv{\text{v}}$

— вектор направления линии и

$P$

точка, принадлежащая правому:

$\vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z) \qquad P(P_x,P_y,P_z)$

Формула векторного уравнения линии :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=(P_x,P_y,P_z)+t\cdot (\text{v}_x,\text{v}_y,\text{v}_z) \end{empheq}$

Параметрические уравнения линии в пространстве

Формулу параметрического уравнения линии можно получить из ее векторного уравнения, приравняв компонент к компоненту:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_x+t\cdot\text{v}_x \\[1.7ex] y=P_y+t\cdot\text{v}_y \\[1.7ex] z=P_z+t\cdot\text{v}_z\end{cases} \end{empheq}$

Непрерывное уравнение линии в пространстве

Формула непрерывного уравнения линии :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_x}{\text{v}_x}=\cfrac{y-P_y}{\text{v}_y}= \cfrac{z-P_z}{\text{v}_z} \end{empheq}$

Этот тип уравнения линии также можно получить из параметрических уравнений, вы можете увидеть демонстрацию на нашей странице непрерывного уравнения , кроме того, вы также сможете увидеть примеры и попрактиковаться с решением уравнений справа.

Общие (или неявные) уравнения линии в пространстве

Наконец, умножив дроби непрерывного уравнения линии два на два, получим общие (или неявные) уравнения линии :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} A_1x+B_1y+C_1z+D_1=0 \\[1.7ex] A_2x+B_2y+C_2z+D_2=0\end{cases} \end{empheq}$

Этот тип уравнения линии также называют декартовым уравнением.

Мы только что рассмотрели 4 наиболее важных уравнения линии (векторное, параметрическое, непрерывное и общее), однако есть еще одно, несколько частное уравнение, и поэтому его объяснение занимает целую страницу. Это каноническое уравнение , по этой ссылке вы можете увидеть все его объяснение, почему оно такое особенное и чем оно отличается от всех остальных.

Плоские уравнения в пространстве

В аналитической геометрии уравнение плоскости — это уравнение, позволяющее аналитически выразить любую плоскость. Итак, чтобы найти уравнение плоскости, нужна только точка и два линейно независимых вектора, принадлежащих этой плоскости.

Таким образом, всеми типами уравнений плоскости являются: векторное уравнение , параметрические уравнения , неявное (или общее) уравнение и каноническое (или сегментное) уравнение плоскости.

Далее мы увидим объяснение и формулы всех уравнений плана.

Векторное уравнение плоскости

Дана точка и два направляющих вектора плоскости:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Формула векторного уравнения плоскости :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y,z)=P+\lambda \vv{\text{u}} + \mu \vv{\text{v}} \end{empheq}$

Или эквивалент:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Золото

$\lambda$

$\mu$

Это два скаляра, то есть два действительных числа.

Параметрические уравнения плоскости

С другой стороны, формула параметрического уравнения плоскости имеет вид:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases} \end{empheq}$

Неявное или общее уравнение плоскости

Неявное уравнение плана, также называемое общим уравнением, получается путем решения следующего определителя и присвоения результату значения 0:

$\displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0$

Таким образом , неявное или общее уравнение результирующего плана будет иметь следующий вид:

Этот тип уравнения плоскости также называется декартовым уравнением плоскости.

Каноническое или сегментное уравнение плоскости

Формула канонического или сегментного уравнения плоскости имеет следующий вид:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cfrac{x}{a}+\cfrac{y}{b} + \cfrac{z}{c} = 1 \end{empheq}$

Золото:

$a$

Это точка пересечения плоскости и оси X.
$b$

Это точка пересечения плоскости и оси Y.
$c$

Здесь плоскость пересекает ось Z.

Вектор нормали к плоскости

Вектор нормали к плоскости — это вектор, перпендикулярный всем прямым, содержащимся в этой плоскости. Следовательно, вектор, нормальный к плоскости, означает, что он перпендикулярен плоскости.

Многие метрические задачи пространственной аналитической геометрии касаются плоскостей и векторов нормалей к ним. Для решения этих упражнений вам просто нужно знать математическую связь между плоскостью и ее вектором нормали:

Компоненты X, Y, Z вектора нормали к плоскости совпадают соответственно с коэффициентами A, B, C неявного (или общего) уравнения этой плоскости.

$\displaystyle \color{orange} \boxed{ \color{black} \quad \pi : \ Ax+By+C+D = 0 \quad \iff \quad \vv{n} = (A,B,C) \quad \vphantom{\Bigl(}}$

Золото

$\vv{n}$

вектор, ортогональный плоскости

$\pi.$

Взаимное положение двух геометрических элементов в пространстве.

Очевидно, что линия или плоскость не обязательно должны быть одни в пространстве, а наоборот, они обычно взаимодействуют друг с другом: пересекаются, параллельны, перпендикулярны и т. д. Что ж, в этом разделе мы увидим различные относительные положения линий и плоскостей и то, как они определяются.

Взаимное положение двух линий в пространстве

В аналитической геометрии при работе в трёхмерном пространстве (в R3) существует 4 возможных относительных положения между двумя прямыми: две прямые могут быть совпадающими , параллельными , секущими или секущими .

Параллельные линии

относительное положение двух параллельных прямых

Две прямые параллельны, если они имеют одно и то же направление, но не имеют общей точки. Кроме того, параллельные линии всегда находятся на одинаковом расстоянии друг от друга.

Совпадающие линии

относительное положение двух совпадающих линий

Две прямые совпадают, если они имеют одинаковое направление и все их точки общие.

Линии пересечения

относительное положение двух пересекающихся линий

Две пересекающиеся прямые имеют разные направления, но соприкасаются в одной точке.

Линии пересечения

Две пересекающиеся прямые имеют разные направления и не пересекаются ни в одной точке. Следовательно, две пересекающиеся линии не лежат в одной плоскости. Например, в графическом представлении над линией

$s$

всегда находится перед прямой линией

$r$

, поэтому они никогда не будут касаться друг друга.

Как найти взаимное положение двух линий по диапазонам

Один из способов найти относительное положение двух строк — вычислить диапазоны двух конкретных матриц, как мы увидим ниже. Этот метод очень полезен, когда две линии выражены в форме неявного (или общего) уравнения.

Таким образом, если у нас есть две линии, выраженные своими неявными (или общими) уравнениями в трехмерном пространстве (в R3):

$\displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0 \end{cases}$

$\displaystyle s: \ \begin{cases}A_3x+B_3y+C_3z+D_3=0 \\[2ex] A_4x+B_4y+C_4z+D_4=0 \end{cases}$

Пусть A — матрица, составленная из коэффициентов двух строк:

$\displaystyle A=\begin{pmatrix}A_1 & B_1 & C_1\\[1.1ex]A_2 & B_2 & C_2\\[1.1ex]A_3 & B_3 & C_3\\[1.1ex]A_4 & B_4 & C_4 \end{pmatrix}$

И учитывая расширенную матрицу A’, которая представляет собой матрицу, сформированную из всех параметров двух строк:

$\displaystyle A'=\begin{pmatrix}A_1 & B_1 & C_1&D_1\\[1.1ex]A_2 & B_2 & C_2&D_2\\[1.1ex]A_3 & B_3 & C_3&D_3\\[1.1ex]A_4 & B_4 & C_4&D_4 \end{pmatrix}$

Затем относительное положение двух строк можно определить по размеру двух предыдущих матриц согласно следующей таблице:

относительные положения двух линий по диапазонам

Следовательно, чтобы найти относительное положение между двумя строками, нам придется вычислить диапазоны обеих матриц, и в зависимости от диапазона каждой матрицы это будет тот или иной случай.

Эту теорему можно доказать с помощью теоремы Руше-Фробениуса (метода, используемого для решения систем линейных уравнений), однако на этой странице мы не будем проводить доказательство, поскольку оно довольно громоздкое и мало что добавляет. .

Взаимное положение двух плоскостей в пространстве

В аналитической геометрии существует только три возможных относительных положения между двумя плоскостями: пересекающиеся плоскости, параллельные плоскости и совпадающие плоскости.

Пересекающиеся плоскости : две плоскости пересекаются, если они пересекаются только по одной прямой.
Параллельные плоскости : Две плоскости параллельны, если они не пересекаются ни в одной точке.
Совпадающие плоскости : две плоскости совпадают, если все точки у них общие.

Пересекающиеся кадры

относительное положение двух пересекающихся плоскостей

параллельные плоскости

относительное положение двух параллельных плоскостей

Соответствующие планы

относительное положение двух совпадающих плоскостей

Как определить взаимное расположение двух плоскостей по коэффициентам

Один из способов узнать относительное положение между двумя плоскостями — использовать коэффициенты их общих (или неявных) уравнений.

Рассмотрим тогда общее (или неявное) уравнение двух разных плоскостей:

$\pi_1 : \ Ax+By+Cz+D=0$

$\pi_2 : \ A'x+B'y+C'z+D'=0$

Относительное положение двух плоскостей в трехмерном пространстве зависит от пропорциональности их коэффициентов или параметров:

взаимное положение двух плоскостей с параметрами

Таким образом, две плоскости пересекутся, когда один из коэффициентов A, B или C не пропорционален остальным. С другой стороны, две плоскости будут параллельны, если только независимые члены не пропорциональны. И наконец, планы совпадут, когда все коэффициенты двух уравнений будут пропорциональны.

Расстояния в космосе

Ниже приведены формулы для расчета расстояния между различными геометрическими элементами: между точкой и линией, между двумя плоскостями, между плоскостью и линией…

Расстояние между двумя точками

Расстояние между двумя точками соответствует норме вектора, определяемого этими двумя точками.

Итак, если у нас есть две общие точки:

$A(a_x,a_y,a_z) \qquad \qquad B(b_x,b_y,b_z)$

Формула расстояния между двумя точками:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(A,B) = \vert \vv{AB} \rvert = \sqrt{(b_x-a_x)^2+(b_y-a_y)^2+(b_z-a_z)^2} \end{empheq}$

Расстояние от точки до линии

Формула расчета расстояния от точки до линии в пространстве:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert} \end{empheq}$

Золото:

$\lvert \vv{\text{v}}_r \rvert$

— модуль вектора направления линии

$r.$
$Q$

это точка справа

$r,$

$P$

точка на линии

$s$

И

$\vv{QP}$

вектор, определенный двумя точками
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

— модуль векторного произведения векторов

$\vv{QP}$

И

$\vv{\text{v}}_r$

Расстояние между двумя линиями

Расстояние между двумя линиями зависит от их взаимного положения:

Если две линии совпадают или пересекаются , расстояние между двумя линиями равно нулю, поскольку они пересекаются (по крайней мере) в одной точке.
Когда две линии параллельны или пересекаются, в зависимости от случая необходимо применить формулу (оба объяснения доступны ниже).

Расстояние между двумя параллельными линиями

Две параллельные прямые всегда находятся на одинаковом расстоянии друг от друга. Итак, чтобы вычислить расстояние между двумя параллельными прямыми в пространстве (в R3) это делается так же, как и в плоскости (в R2): вам просто нужно взять точку на одной из двух прямых и найти расстояние там. это от этой точки до другой линии.

Итак, чтобы определить расстояние между двумя параллельными прямыми, необходимо использовать формулу расстояния между точкой и прямой.

Расстояние между двумя пересекающимися линиями

Пусть вектор направления и любая точка двух пересекающихся прямых будут:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

Формула расстояния между двумя пересекающимися линиями:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} \end{empheq}$

Золото:

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

— абсолютное значение смешанного произведения векторов

$\vv{\text{u}}, \vv{\text{v}}$

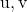
и вектор, определяемый точками

$A$

И

$B$

.
$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

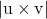
— модуль векторного произведения между векторами направления двух пересекающихся линий.

Хотя у вас есть формула, определить расстояние между двумя пересекающимися линиями сложнее, чем кажется. Итак, если вы хотите потренироваться, по следующей ссылке вы можете увидеть примеры и решенные упражнения на расстояние между двумя пересекающимися линиями.

Расстояние от точки до плоскости

Дана точка и общее (или неявное) уравнение плоскости:

$P(x_0,y_0,z_0) \qquad \qquad \pi: \ Ax+By+Cz+D=0$

Формула расстояния от точки до плоскости:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle d(P,\pi) = \cfrac{\lvert A\cdot x_0+B\cdot y_0+C\cdot z_0+D\rvert}{\sqrt{A^2+B^2+C^2}} \end{empheq}$

Если, применив формулу, мы получим результат, равный нулю, это, очевидно, означает, что расстояние между точкой и плоскостью равно нулю и, следовательно, точка является частью этой плоскости.

Расстояние между двумя плоскостями

Расстояние между двумя плоскостями в пространстве зависит от взаимного положения этих двух плоскостей:

Если две плоскости пересекаются или совпадают , расстояние между ними равно нулю, поскольку они пересекаются в определенной точке.
Если две плоскости параллельны , расстояние между двумя плоскостями рассчитывается путем взятия точки на одной из двух плоскостей и вычисления расстояния между этой точкой и другой плоскостью.

Расстояние между двумя параллельными плоскостями

Две параллельные плоскости всегда находятся на одинаковом расстоянии друг от друга, поэтому, чтобы найти расстояние между двумя параллельными плоскостями, мы можем взять точку на одной из двух плоскостей и вычислить расстояние от этой точки до другой плоскости.

Итак, чтобы вычислить расстояние между двумя параллельными плоскостями, вы должны найти точку на одной из двух плоскостей, а затем использовать формулу расстояния между точкой и плоскостью.

Углы в пространстве

Как и в случае с расстояниями, определение угла между двумя геометрическими объектами в пространстве зависит от их геометрических характеристик. Потому что вычисление угла, образованного двумя прямыми, — это не то же самое, что вычисление угла, образованного двумя плоскостями. Ниже приведены формулы для нахождения углов между прямыми и плоскостями.

Угол между двумя линиями

Чтобы узнать угол между двумя линиями в евклидовом пространстве, мы должны вычислить угол, образованный их векторами направления, поэтому:

Учитывая векторы направления двух разных линий:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y,\text{u}_z)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

Угол, образованный этими двумя линиями, можно рассчитать по следующей формуле:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

Золото

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

являются модулями векторов

$\vv{\text{u}}$

$\vv{\text{v}}$

соответственно.

Напомним, что формула модуля вектора имеет вид:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Угол между двумя плоскостями

Угол между двумя плоскостями равен углу, образованному векторами нормалей к указанным плоскостям. Поэтому, чтобы найти угол между двумя плоскостями, мы вычисляем угол, образованный их векторами нормалей, так как они эквивалентны .

Учитывая общее (или неявное) уравнение двух разных плоскостей:

$\pi_1 : \ A_1x+B_1y+C_1z+D_1=0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2=0$

Нормальный вектор каждой плоскости:

$\vv{n}_1=(A_1,B_1,C_1)$

$\vv{n}_2=(A_2,B_2,C_2)$

А угол, образованный этими двумя плоскостями, определяется путем вычисления угла, образованного их векторами нормалей, по следующей формуле:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \cos(\alpha) =\cfrac{\lvert \vv{n}_1 \cdot \vv{n}_2\rvert}{\lvert \vv{n}_1 \rvert \cdot \lvert \vv{n}_2 \rvert} \end{empheq}$

Угол между линией и плоскостью

Угол, образованный линией и плоскостью, определяется как меньший из двух дополнительных углов, образованных вектором направления линии и вектором нормали к плоскости.

Следовательно, если

$\vv{\text{v}}$

— вектор направления линии и

$\vv{n}$

– вектор, нормаль к плоскости:

$\vv{\text{v}} = (\text{v}_x,\text{v}_y,\text{v}_z)$

$\vv{n}=(n_x,n_y,n_z)$

Формула, используемая для расчета угла, образованного линией и плоскостью:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \text{sen}(\alpha)=\cfrac{\lvert \vv{\text{v}} \cdot \vv{n}\rvert}{\lvert \vv{\text{v}} \rvert \cdot \lvert \vv{n} \rvert} \end{empheq}$

Аналитическая геометрия в пространстве (формулы)

Что такое геометрия в пространстве?

Уравнения линии в пространстве

Векторное уравнение линии в пространстве

Параметрические уравнения линии в пространстве

Непрерывное уравнение линии в пространстве

Общие (или неявные) уравнения линии в пространстве

Плоские уравнения в пространстве

Векторное уравнение плоскости

Параметрические уравнения плоскости

Неявное или общее уравнение плоскости

Каноническое или сегментное уравнение плоскости

Вектор нормали к плоскости

Взаимное положение двух геометрических элементов в пространстве.

Взаимное положение двух линий в пространстве

Как найти взаимное положение двух линий по диапазонам

Взаимное положение двух плоскостей в пространстве

Как определить взаимное расположение двух плоскостей по коэффициентам

Расстояния в космосе

Расстояние между двумя точками

Расстояние от точки до линии

Расстояние между двумя линиями

Расстояние между двумя параллельными линиями

Расстояние между двумя пересекающимися линиями

Расстояние от точки до плоскости

Расстояние между двумя плоскостями

Расстояние между двумя параллельными плоскостями

Углы в пространстве

Угол между двумя линиями

Угол между двумя плоскостями

Угол между линией и плоскостью

Оставьте комментарий Отменить ответ