▷ Как узнать, совпали ли 3 (или более) точки? ✅

На этой странице вы найдете объяснение того, что такое выровненные точки. Вы также увидите все доступные методы, позволяющие определить, совмещены ли 3 (или более) точки. Более того, вы найдете несколько примеров и даже решенных упражнений, чтобы можно было попрактиковаться.

Что значит, что точки совпадают?

В аналитической геометрии три или более точки считаются выровненными, если все они лежат на одной линии, то есть если их можно соединить, проведя между ними прямую линию.

Очевидно, что 2 точки всегда будут совмещены, поскольку между двумя точками всегда можно провести линию. Однако три точки не обязательно должны находиться на одной линии. В основном существует два способа узнать, совпадают ли 3 или более точки:

Векторный метод : состоит в проверке того, пропорциональны ли векторы, образующие точки.
Метод уравнения линии : он заключается в определении принадлежности точек одной линии.

Ниже приводится объяснение каждой процедуры и примеры, чтобы вы могли решить, какая из них лучше для вас.

Как определить, выровнены ли 3 (или более) точки с помощью векторного метода

Учитывая три момента:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Три точки совпадают, если векторы

$\vv{AB}$

$\vv{BC}$

они имеют одинаковое направление, то есть пропорциональны ли их компоненты.

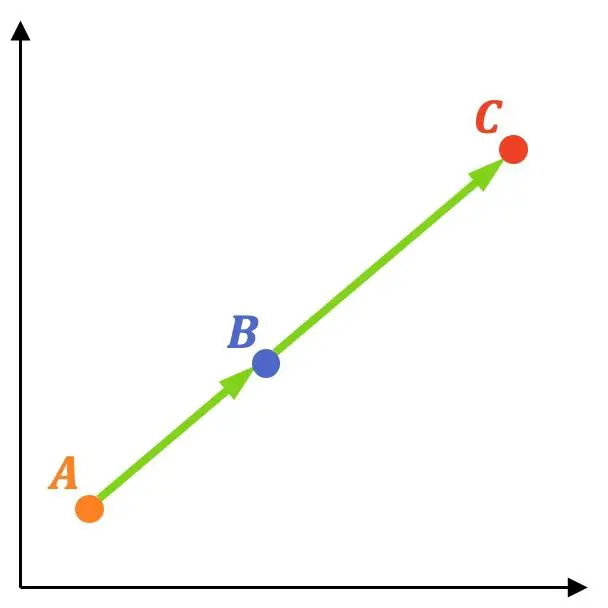
Давайте посмотрим на примере, как это делается:

Определите, совпадают ли следующие 3 точки:

$A(1,2) \quad B(4,4) \quad C(-2,0)$

Сначала вычисляем векторы между точками. Достаточно рассчитать два разных вектора:

$\vv{AB} = B - A = (4,4)- (1,2) = (3,2)$

$\vv{BC} = C-B =(-2,0)- (4,4)= (-6,-4)$

А затем проверяем, пропорциональны ли координаты векторов:

$\cfrac{-6}{3} = \cfrac{-4}{2} = -2$

Разделив компоненты X и компоненты Y двух векторов, мы получаем один и тот же результат (-2), поэтому векторы имеют одинаковое направление и, следовательно, точки выровнены .

Этот метод также можно использовать, чтобы узнать, выровнены ли три или более точки в пространстве (в R3), единственное, что нужно добавить, это проверить, что третья компонента двух векторов (компонент Z) также пропорциональна.

Если эта статья вам полезна, вам, вероятно, также будет интересно узнать, как вычислить среднюю точку между двумя точками , поскольку, очевидно, нахождение средней точки из двух точек — это способ определить третью точку, совмещенную с двумя другими точками. Вы можете увидеть, как это делается, на связанной странице, кроме того, вы также сможете увидеть примеры и упражнения, решаемые шаг за шагом.

Как определить, выровнены ли 3 (или более) точки, с помощью метода уравнения прямой линии

Как мы только что видели в предыдущем разделе, один из способов изучить выравнивание трех или более точек — использовать векторы, которые могут образовываться между ними. Ну, другой метод — начать с уравнения прямой:

Учитывая три момента:

$A(x_1,y_1) \quad B(x_2,y_2) \quad C(x_3,y_3)$

Три точки совпадают, если все они принадлежат одной линии. Поэтому, чтобы узнать, совпадают ли три или более точки, необходимо выполнить следующие шаги:

Найдите уравнение прямой, проходящей через две из трех точек.
Проверьте, принадлежит ли третьей точке линия. В данном случае это означает, что три точки выровнены, однако если условие не выполняется, это означает, что точки не выровнены.

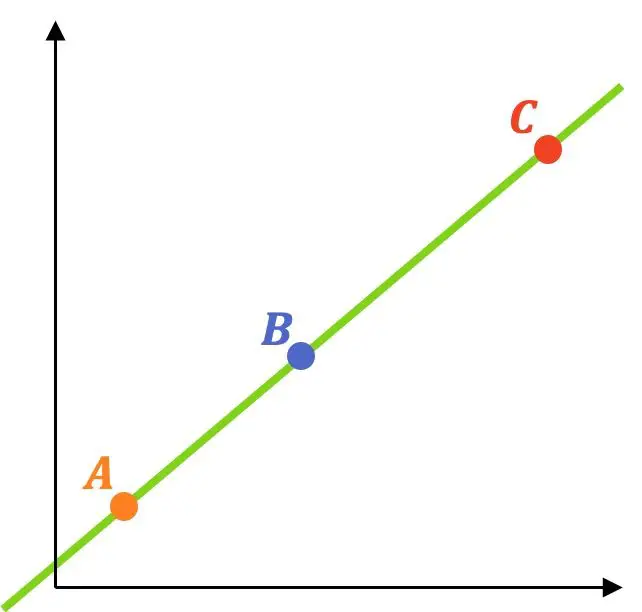
В качестве примера решим упражнение таким методом:

Убедитесь, что следующие 3 точки совпадают:

$A(3,1) \quad B(1,4) \quad C(5,-2)$

Прежде всего, мы должны вычислить уравнение линии, проходящей через точки A и B. Таким образом, мы находим вектор направления линии:

$\vv{AB} = B-A = (1,4) - (3,1) = (-2,3)$

Теперь вам предстоит построить уравнение линии, вы можете выбрать нужный вам тип: параметрическое, неявное, общее и т.д. Но в данном случае мы будем использовать непрерывное уравнение. Таким образом, непрерывное уравнение прямой, проходящей через точку А и точку В, будет иметь вид:

$\cfrac{x-3}{-2}=\cfrac{y-1}{3}$

Получив уравнение линии, мы должны проверить, принадлежит ли другая точка той же прямой. Для этого подставим координаты точки С в уравнение линии:

$\cfrac{5-3}{-2}=\cfrac{-2-1}{3}$

$\cfrac{2}{-2}=\cfrac{-3}{3}$

$-1=-1$

У нас ничья, значит, точка удовлетворяет уравнению прямой. Следовательно, эти 3 точки лежат на одной прямой .

Следует отметить, что набор совмещенных точек не обязательно должен быть равноудаленным, то есть расстояние между несколькими совмещенными точками может быть разным. Разницу между двумя понятиями вы можете увидеть в объяснении расстояния между двумя точками (геометрия) , где также можно увидеть примеры и упражнения, решаемые шаг за шагом.

Решенные упражнения с выровненными точками

Упражнение 1

Определите, совпадают ли следующие 3 точки:

$A(1,1) \quad B(2,-1) \quad C(-2,7)$

Посмотреть решение

Мы можем выбрать один из двух рассмотренных нами методов решения проблемы. В данном случае мы будем использовать векторный метод.

Сначала вычисляем векторы между точками:

$\vv{AB} = B - A = (2,-1)- (1,1) = (1,-2)$

$\vv{BC} = C-B =(-2,7)- (2,-1)= (-4,8)$

А теперь проверим, пропорциональны ли декартовы координаты векторов:

$\cfrac{-4}{1} = \cfrac{8}{-2} = -4$

Разделив компоненты X и компоненты Y двух векторов друг на друга, мы получаем один и тот же результат (-4), поэтому векторы имеют одинаковое направление. Факт, который указывает на то, что точки совпадают .