Совершенный квадратный трехчлен

На этой странице мы объясним, что такое идеальный квадратный трехчлен и как он рассчитывается. Кроме того, вы сможете увидеть несколько примеров и попрактиковаться с пошаговыми упражнениями для идеального квадратного трехчлена.

Что такое идеальный квадратный трехчлен?

Очевидно, что прежде чем понять значение идеального квадратного трехчлена, вам необходимо знать, что такое трехчлены , поэтому я рекомендую взглянуть на эту связанную страницу (где это подробно объяснено), прежде чем продолжить.

Итак, определение идеального квадратного трехчлена выглядит следующим образом:

В математике идеальный квадратный трёхчлен , также известный как TCP , — это трёхчлен, полученный возведением в квадрат бинома.

Следовательно, идеальный квадратный трехчлен состоит из многочлена с двумя точными квадратами и еще одним членом, который представляет собой двойное произведение оснований этих квадратов.

Как видно из двух приведенных выше формул, идеальный квадратный трехчлен получается из двух известных тождеств (или известных произведений), поэтому он так важен. В частности, идеальный квадратный трехчлен находится при решении квадрата сложения или квадрата вычитания .

Примеры идеального квадратного трехчлена

Чтобы завершить понимание концепции идеального квадратного трехчлена, мы шаг за шагом объясним два примера:

Пример 1

Этот пример представляет собой идеальный квадратный трехчлен, поскольку в его алгебраическом выражении имеются два совершенных квадрата (т. е. они имеют точный квадратный корень), поскольку

и 9 эквивалентны

и 3, возведенные соответственно в степень двойки:

И еще, последний оставшийся член трехчлена

Его получают умножением оснований двух предыдущих квадратов вместе и на 2:

Таким образом, вся примечательная идентичность в этом упражнении будет такой:

Пример 2

Этот другой пример также является идеальным квадратным трехчленом, поскольку соблюдены 3 необходимых условия: два члена соответствуют двум идеальным квадратам, а другой член является результатом умножения оснований этих квадратов друг на друга и на 2.

В этом случае идеальный квадратный трехчлен имеет отрицательный моном, поэтому он соответствует развитию заметного равенства квадрата разности:

Как факторизовать идеальный квадратный трехчлен

В алгебре очень распространенной проблемой является факторизация совершенного квадратного трехчлена (PCT). Если вы не знаете, что это значит, факторизация многочлена означает преобразование его выражения в произведение множителей.

Таким образом, чтобы факторизовать этот тип алгебраического трехчлена, необходимо соблюдать следующие правила:

1. Трехчлен должен иметь два полных квадрата, которые мы будем называть

   

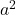
   И

   

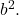
2. Третий оставшийся член трехчлена должен быть равен двойному произведению оснований двух полных квадратов, что математически соответствует выражению

   

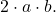
3. Факторизованный трехчлен будет

   

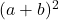
   если все члены идеального квадратного трехчлена положительны, в противном случае, если двойное произведение оснований квадратов имеет отрицательный знак, факторизованный трехчлен будет равен

   

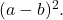
Чтобы закончить понимание процедуры, шаг за шагом решим упражнение:

• Разложите на множители следующий идеальный квадратный трехчлен:

Первое, что нам нужно сделать, это определить, есть ли в трехчлене два элемента, которые являются точными квадратами, или, другими словами, не дает ли его квадратный корень десятичное число. В этой проблеме

— квадрат переменной

а 36 — это квадрат 6:

Таким образом, трехчлен имеет два полных квадрата.

Во-вторых, мы должны проверить, эквивалентен ли промежуточный член двойному произведению двух корней, вычисленному на предыдущем шаге:

Это правило также соблюдается.

Тогда все условия соблюдены. Следовательно, факторизованный совершенно квадратный трехчлен — это бином, образованный двумя найденными корнями (

и число 6) в квадрате:

Так как промежуточный член отрицательный, то в скобках тоже надо поставить знак минус. С другой стороны, если бы оно было положительным, нам пришлось бы добавить сумму:

С логической точки зрения факторизация — это сложная процедура, поэтому в дополнение к попыткам выполнить приведенное ниже упражнение я рекомендую взглянуть на эти примеры факторизации полиномов . По этой ссылке мы также объясняем метод, который используется не только для факторизации трехчленов, но и для полиномов любого типа, и так же быстро.

Решенные упражнения идеального квадратного трёхчлена

Преобразуйте следующие трехчлены в квадратные биномы, применив соответствующую формулу:

Чтобы преобразовать идеальный квадратный трехчлен в степень квадратного бинома, вы должны использовать формулы для примечательных тождеств квадрата суммы и квадрата разности, а именно:

Еще:

⬇⬇⬇ Не забывайте, что все свои вопросы вы можете написать нам ниже в комментариях! ⬇⬇⬇