Полиномиальное разложение (или выражение) числа

На этой странице мы объясняем, как выполнить полиномиальное разложение (или выражение) числа. Здесь вы можете увидеть примеры полиномиальных разложений, а также найти решенные пошаговые упражнения для практики.

Что такое полиномиальное разложение числа?

В математике полиномиальное разложение числа состоит из выражения этого числа в сумме, так что каждый член суммы является произведением каждой цифры числа на степень по основанию 10.

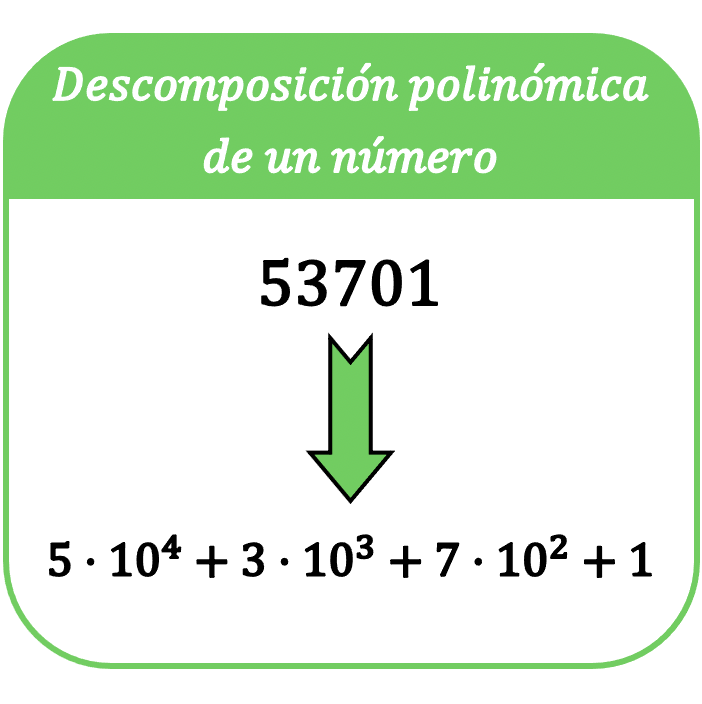
Термин полиномиальное разложение числа также известен как полиномиальное выражение числа .

Как выполнить полиномиальное разложение

Чтобы выполнить полиномиальное разложение числа, необходимо каждую цифру числа умножить на 10, возведенную в число цифр справа .

Например, если мы хотим вычислить полиномиальное разложение следующего числа:

В данном случае число 8 занимает пятую позицию, поэтому справа от него есть 4 цифры. Поэтому нам нужно умножить восемь на десять в четвёртой степени:

Таким образом, чтобы полиномиально разложить число 86293 необходимо проделать то же самое со всеми цифрами числа, а все умножения выразить в виде суммы:

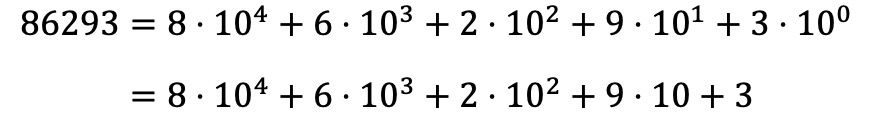
Обратите внимание, что степень 10 ⁰ исчезает, поскольку по свойствам степеней любое число, возведенное в 0, равно 1, поэтому 10 ⁰ =1.

С другой стороны, найти полиномиальное разложение числа можно и из его мультипликативного разложения:

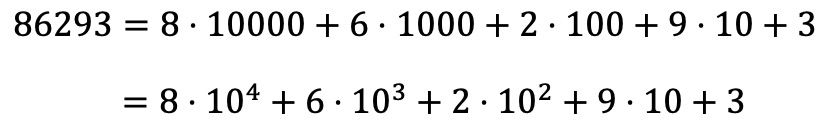
Примеры полиномиальных разложений чисел

Увидев, как осуществляется полиномиальное разложение числа, мы увидим различные примеры операций этого типа, чтобы полностью понять эту концепцию.

• Полиномиальное разложение 3641:

• Полиномиальное разложение 56912:

• Полиномиальное разложение 27084:

В этом последнем примере мы можем упростить третье умножение, поскольку любое число, умноженное на ноль, сокращается.

Полиномиальное разложение десятичных чисел

Мы только что увидели, как выполнять полиномиальное разложение натуральных чисел. Но… как разложить десятичное число полиномиально?

Ну, разложение многочлена с десятичными числами выполняется так же, как и с целыми числами, но, кроме того, мы складываем произведение каждой десятичной цифры, умноженное на степень по основанию 10, показатель которой — это десятичная позиция, занимаемая указанной цифрой с отрицательным знаком. знак.

Объяснение на словах может показаться очень сложным, но вы увидите, что на примере это будет лучше понятно:

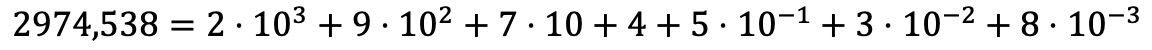
Решенные упражнения на полиномиальное разложение

Чтобы вы могли попрактиковаться в разложении полиномов, мы подготовили несколько упражнений, решаемых шаг за шагом.

Не забывайте, что любые вопросы вы можете задать нам в комментариях! 🤔🤔🤔

Упражнение 1

Выполните полиномиальное разложение следующих чисел:

Чтобы найти полиномиальное разложение любого числа, умножьте каждую цифру этого числа на 10 на количество цифр справа, а затем сложите все умножения. Еще:

Упражнение 2

Найдите полиномиальное разложение следующих чисел:

Чтобы полиномиально разложить число, необходимо каждую цифру указанного числа умножить на десять на количество цифр справа от нее, а затем сложить все произведения. Еще:

Упражнение 3

Вычислите полиномиальное разложение следующих десятичных чисел:

В этой задаче все числа десятичные, поэтому для их разложения вы должны умножить каждую недесятичную цифру на 10, возведя ее до количества цифр, которые она имеет до десятичной точки, и умножить каждую десятичную цифру на 10, возведенную в десятичную позицию, с помощью отрицательный знак.