Бином ньютона (биномиальная теорема)

На этой странице вы найдете объяснение того, что такое бином Ньютона (или биномиальная теорема) и какова его формула. Вы также можете увидеть, как это можно упростить с помощью треугольника Тартальи (или Паскаля). Кроме того, вы найдете пошаговые решения упражнений для бинома Ньютона и всех его свойств. Наконец, мы объясним курьезы, лежащие в основе происхождения этой очень конкретной теоремы.

Что такое бином Ньютона?

В математике бином Ньютона , также известный как теорема о биноме , представляет собой формулу, позволяющую легко вычислить степень бинома. Другими словами, бином Ньютона состоит из формулы, с помощью которой можно решить алгебраические выражения вида (a+b).

Очевидно, эта теорема названа в честь физика, математика и философа сэра Исаака Ньютона. Однако в этом отношении существуют некоторые разногласия, поскольку были найдены ближневосточные тексты, в которых эта теорема уже использовалась. Ниже мы подробно обсудим происхождение этой математической формулы.

Биномиальная формула Ньютона

Как мы видели в определении бинома Ньютона, эта теорема используется для решения степеней биномов. Но… как применяется бином Ньютона? Или, другими словами, что такое биномиальная формула Ньютона?

Математическая формула бинома Ньютона выглядит следующим образом:

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

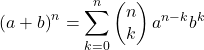
Или эквивалент:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

Формула немного сложна для понимания концепции бинома Ньютона, поэтому мы представили ниже степени биномов низшей степени, чтобы вы могли ее лучше понять:

формула биномиальной теоремы Ньютона

Как видите, при разложении бинома показатели первого слагаемого (а) уменьшаются, а показатели второго слагаемого (б) увеличиваются , так же, как увеличивается младший элемент комбинаторных чисел.

Следовательно, чтобы использовать биномиальную теорему, нужно уметь решать комбинаторное число, то есть алгебраическое выражение вида

\begin{pmatrix} 4 \\ 2 \end{pmatrix}

. Итак, прежде чем мы рассмотрим примеры расчета бинома Ньютона, давайте кратко рассмотрим комбинаторные числа.

комбинаторное число

Для определения комбинаторного числа (или биномиального коэффициента) необходимо применить следующую формулу:

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

Золото

n!

И

k!

Это факториалы . Давайте также вспомним, что факториал вычисляется путем умножения всех натуральных чисел, равных 1, на указанное число:

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

В качестве примера мы найдем комбинаторное число, чтобы вы могли увидеть, как это делается:

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

Комбинаторные числа можно определить и через калькулятор с помощью клавиши

\boxed{nCr}.

Биномиальные примеры Ньютона

Теперь, когда мы знаем, что такое биномиальная теорема, давайте посмотрим, как применить биномиальную формулу Ньютона, на двух числовых примерах.

Пример 1

  • Примените бином Ньютона, чтобы вычислить степень следующего бинома:

(x+3)^2

Очевидно, что, поскольку этот бином возведен в квадрат, его также можно решить с помощью формул для примечательных тождеств ( как решить примечательные тождества ), но мы вычислим его на примере биномиальной теоремы.

Прежде всего, мы должны применить биномиальную формулу Ньютона:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

В данном случае n=2, следовательно:

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

Посмотрите внимательно, вначале мы поднимаем первое слагаемое (x) до максимально возможного, что в данном случае равно 2. С другой стороны, мы поднимаем второе слагаемое (3) до минимально возможного, которое всегда равно 0. Но по мере того, как мы движемся вправо, нам нужно увеличить первый член до меньшего числа, чем раньше, а второй член до большего числа, чем раньше.

Теперь посчитаем комбинаторные числа:

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

Решаем для полномочий:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

И наконец, посчитаем умножения:

\left( x+3\right)^2 =x^2 + 6x + 9

Пример 2

Теперь мы собираемся решить немного более сложную задачу.

  • Примените формулу бинома Ньютона, чтобы найти степень следующего бинома:

(2x+1)^3

Формула биномиальной теоремы:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

В данном случае n=3, следовательно:

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

Вычисляем комбинаторные числа:

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

Теперь решаем степени, для этого важно запомнить следующие два свойства:

• Когда моном возводится в степень, коэффициент и переменная возводятся в одну и ту же степень →

(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• Любой член, доведенный до 0, дает 1 →

(2x)^0=1

Таким образом, мы находим степени через эти два свойства:

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

И, наконец, умножаем слагаемые:

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

Бином Ньютона и треугольник Тартальи (или Паскаля)

Как вы видели в приведенных выше примерах, вычисление комбинаторных чисел немного утомительно. Именно поэтому мы собираемся научить вас трюку, чтобы вам не приходилось решать комбинаторные числа, поскольку вы можете напрямую узнать, сколько они стоят, используя треугольник Тартальи, также известный как треугольник Паскаля.

Если вы не знаете, что это такое, треугольник Тартальи , также называемый треугольником Паскаля , представляет собой математическое представление чисел, расположенных в форме треугольника.

Чтобы построить треугольник Тартальи или Паскаля, мы должны начать с вершины треугольника, которая всегда равна 1, а затем определить номера строк ниже. Каждое число в следующих строках равно сумме двух чисел, находящихся непосредственно над ним, за исключением концов строк, которые всегда равны 1.

Ньютон пара 1 средняя школа онлайн

Итак, каждое из этих чисел в треугольнике Тартальи соответствует результату комбинаторного числа, посмотрите на следующий рисунок:

Например, биномиальный коэффициент

\begin{pmatrix} 3 \\ 1 \end{pmatrix}

эквивалентно 3, поскольку в треугольнике Тартальи на его позиции стоит цифра 3.

Поэтому мы можем использовать треугольник Тартальи (или Паскаля) для решения бинома Ньютона гораздо быстрее, поскольку он избавляет нас от вычислений комбинаторных чисел.

Например, если мы хотим выполнить следующее потенцирование бинома:

(x+5)^3

Применяя биномиальное правило Ньютона, мы получаем следующее алгебраическое выражение:

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

Что ж, вместо того, чтобы вычислять комбинаторные числа одно за другим, мы можем просто заменить каждое комбинаторное число соответствующим коэффициентом треугольника Тартальи. В этом случае бином поднимается до 3-го уровня, следовательно, он соответствует третьему уровню треугольника:

Тарталья или треугольник Паскаля и бином Ньютона

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

И теперь нам остаётся только проделать оставшиеся операции:

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

Как видите, треугольник Тартальи (или Паскаля) используется для вычисления бинома Ньютона более простым и быстрым способом, как мы показали. Именно поэтому мы рекомендуем его использовать.

Подводя итог всему, что мы видели до сих пор, мы оставляем вам изображение, показывающее, как выглядят выражения биномов Ньютона с числами треугольника Тартальи (или Паскаля):

Бином Ньютона и треугольник Паскаля или Тарталья

Отрицательный бином Ньютона: степень вычитания

До сих пор все примеры бинома Ньютона, которые мы решили, были сложением. С другой стороны, когда один из двух членов бинома имеет отрицательный знак, процедура остается аналогичной, но немного меняется.

Когда один из членов бинома Ньютона отрицателен, то есть представляет собой вычитание типа (ab) n , знаки разложения бинома Ньютона должны чередоваться в виде + – + – + – + – …

Ниже мы развили степени отрицательных биномов первых 5 степеней с помощью биномиальной теоремы и уже имеющихся коэффициентов треугольника Тартальи, чтобы вы могли напрямую найти нужное вам биномиальное выражение:

отрицательная биномиальная степень Ньютона вычитания 2

Свойства бинома Ньютона

Биномиальные выражения Ньютона имеют следующие характеристики:

  • Разложение бинома Ньютона всегда дает на один член больше, чем степень бинома. Или, другими словами, для пары

    (a+b)^n

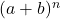
    они затронуты

    n+1

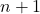
    условия.

  • Силы стихии

    a

    Начните с

    n

    и они уменьшаются, пока не достигнут 0 в последнем квартале.

  • Силы стихии

    b

    они идут в другом направлении: начинаются с 0 и увеличиваются, пока не достигнут

    n

    в последний срок.

  • Для каждого элемента бинома Ньютона сумма показателей степени

    a

    И

    b

    равно

    n.

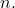
  • Коэффициент при первом члене биномиального выражения Ньютона всегда равен 1 (положительный), а второй коэффициент эквивалентен показателю бинома (положительному или отрицательному).

Вычислите k-й член бинома Ньютона.

Хотя это необычно, иногда мы можем столкнуться с проблемами, в которых вместо биномиального разложения Ньютона нас просят определить k-й член бинома Ньютона, то есть член, который занимает позицию k.

Таким образом, чтобы вычислить член, занимающий место k в биноме Ньютона, мы должны использовать формулу, которая зависит от того, является ли бином сложением или вычитанием:

  • Если бином Ньютона положителен, значение k-го члена рассчитывается по следующей формуле:

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • Если бином Ньютона отрицательный, значение k-го члена определяется по следующей формуле:

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

В качестве примера найдем четвертый член следующего бинома 5-й степени:

(x+3)^5

Поскольку это бином, состоящий из суммы, применим первую формулу:

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

Заменим переменные в формуле соответствующими значениями:

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

И делаем операции:

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

Таким образом, мы вычислили четвертый член биномиального разложения Ньютона без необходимости вычисления всех остальных членов.

Решенные упражнения для бинома Ньютона

Теперь, когда мы объяснили, что такое биномиальная теорема, мы оставляем вам несколько решенных пошаговых упражнений с биномом Ньютона, чтобы вы могли попрактиковаться. Также помните, что любые вопросы и предложения вы можете оставить нам в комментариях.

Упражнение 1

Разложите следующую биномиальную степень, используя биномиальную теорему:

(x+4)^3

Сначала воспользуемся биномиальной формулой Ньютона:

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

Поскольку бином возведен в степень 3, мы смотрим на третий уровень треугольника Тартальи, чтобы непосредственно найти комбинаторные числа:

Упражнения по биномиальной теореме Ньютона решены шаг за шагом 1 средняя школа

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

Мы осуществляем полномочия:

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

И, наконец, умножаем:

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

Упражнение 2

Рассчитайте следующую степень по биномиальной формуле Ньютона:

(3x+2)^3

Сначала применим биномиальную формулу Ньютона:

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

Поскольку бином возведен в куб, мы смотрим на третий уровень треугольника Паскаля, чтобы непосредственно узнать значения комбинаторных чисел:

Упражнения по биномиальной теореме Ньютона решены шаг за шагом 1 средняя школа

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

Вычисляем степени мономов:

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

И, наконец, делаем умножения:

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

Упражнение 3

Разверните следующее полиномиальное выражение, используя биномиальную формулу Ньютона:

(2x-2)^3

Сначала воспользуемся биномиальной формулой Ньютона. Но так как внутри скобок у нас идет вычитание, то надо чередовать знаки коэффициентов каждого слагаемого:

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

Поскольку бином возведен в степень тройки, мы смотрим на третий уровень треугольника Тартальи, чтобы непосредственно вычислить комбинаторные числа:

Упражнения по биномиальной теореме Ньютона решены шаг за шагом 1 средняя школа

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

Мы осуществляем полномочия:

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

И решаем умножение:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

Упражнение 4

Найдите расширенное выражение следующего бинома Ньютона по формуле:

(4x-3y)^4

Надо применить общую формулу бинома Ньютона, но так как в данном случае в скобках стоит вычитание, то надо чередовать знаки каждого слагаемого:

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

Поскольку бином возведен в четвертую ступень, мы смотрим на уровень 4 треугольника Тартальи, чтобы напрямую найти комбинаторные числа:

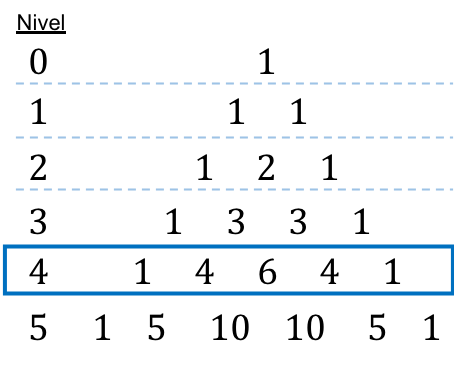
Биномиальная пирамида Ньютона

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

Мы реализуем все возможности:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

И, наконец, решаем умножение:

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

Упражнение 5

Определите седьмой член разложения следующего биномиального выражения:

(2x-5y)^{10}

Поскольку это отрицательный бином, мы должны использовать следующую формулу:

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Мы хотим определить член 7, и бином возводится в степень 10, поэтому, подставив значения в формулу, получится:

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

Поэтому для работы достаточно знать термин:

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

История бинома Ньютона

Хотя происхождение биномиальной теоремы приписывают известному английскому учёному Исааку Ньютону (1642-1727), на самом деле первая формулировка теоремы была впервые открыта персидским инженером Аль-Кариджи около 1000 года. И даже было обнаружено, что В XIII веке китайские математики Ян Хуэй и Чу Ши-Чье уже знали биномиальные разложения малых степеней.

Позже, в 17 веке, Ньютон на основе фундамента, заложенного предыдущими математиками, расширил биномиальную теорему. Используя методы интерполяции и экстраполяции математика Джона Уоллса, а также концепции обобщенных показателей, он смог преобразовать полиномиальное выражение в бесконечный ряд.

Примерно в 1665 году Ньютону удалось продемонстрировать, что показатель n биномиальной теоремы также может быть рациональным показателем, то есть, что степень бинома также может быть решена, если показатель степени является дробью. С другой стороны, это было доказано и в случае отрицательного показателя. И, что удивительно, он обнаружил, что развитие этих двух выражений представляет собой бесконечный ряд членов.

Именно с этим открытием Ньютон начал подвергать сомнению связь между бесконечными рядами и конечными полиномиальными выражениями и пришел к выводу, что математические операции могут выполняться с бесконечными рядами так же, как и с конечными полиномиальными выражениями. Хотя Ньютон никогда не публиковал эту теорему, Джон Уоллс в конце концов сделал это в 1685 году, приписав это открытие Ньютону.

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх