На этой странице вы узнаете, что это такое и как вычислить числовое значение многочлена. Кроме того, вы сможете увидеть примеры и упражнения, пошагово решающие числовое значение многочлена.
Каково числовое значение многочлена?
В математике числовое значение многочлена P(x) для значения x=a, то есть P(a), представляет собой результат, полученный заменой переменной x многочлена на число a и выполнением указанных вычислений. в полиномиальном выражении.
Чтобы вы могли лучше понять понятие числового значения многочлена, ниже покажем, как оно рассчитывается на примере:
Как вычислить числовое значение многочлена
Теперь, когда мы знаем математическое определение числового значения многочлена, давайте посмотрим, как определить числовое значение многочлена на примере:
- Каково числовое значение следующего многочлена для x=2?
![]()
Чтобы найти числовое значение многочлена, необходимо оценить этот многочлен в значении, заданном задачей, то есть необходимо подставить переменную
![]()
полинома по значению утверждения. Поэтому в данном случае нам нужно заменить букву
![]()
Для двоих:
![]()
И как только мы подставим значение в алгебраическое выражение многочлена, мы выполняем операции. Итак, сначала находим степени:
![]()
Теперь посчитаем умножения:
![]()
И, наконец, складываем и вычитаем слагаемые:
![]()
В заключение, численное значение полинома при x=2 равно 21.
Как видите, найти числовое значение многочлена не очень сложно, но оно имеет несколько очень полезных приложений. Например, знание того, как найти числовое значение многочлена, необходимо для использования теоремы об остатках, очень важной теоремы о многочленах. Нажмите на эту ссылку и узнайте , что такое теорема об остатках , вы найдете ее объяснение, примеры использования и пошагово решенные упражнения.
Примеры числовых значений полиномов
Чтобы вы поняли, как получить числовое значение многочлена, мы оставляем вам другие решенные примеры:
Пример 1
- Вычислить числовое значение многочлена
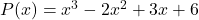
Для

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
В этом случае числовое значение многочлена равно 0. Это имеет последствия, обусловленные свойствами многочленов, поскольку благодаря факторной теореме мы можем знать, каким будет остаток от определенных делений между многочленами. Чтобы узнать больше, нажмите на предыдущую ссылку, где мы объясняем, что это за теорема и для чего она нужна.
Пример 2
- Определить числовое значение многочлена
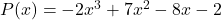
Для
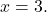
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
Пока мы рассмотрели только то, как определить числовое значение многочлена классическим способом, но следует знать, что существует и другой метод. Более конкретно, вы также можете вычислить числовое значение полинома с помощью метода Руффини . Вы также должны знать, как использовать эту процедуру, поэтому мы рекомендуем ознакомиться с ее подробным объяснением по ссылке.
Числовое значение полинома с двумя или более переменными
Мы только что увидели, как найти числовое значение многочлена, если он имеет только одну переменную. Но… как получить числовое значение многочлена, если у него более одной переменной?
Ну а если в многочлене 2 и более букв, то его числовое значение должно быть вычислено таким же образом, т.е. сначала заменить каждую переменную в многочлене соответствующим значением, а затем решать полиномиальные операции .
Например, у вас есть проблема такого типа, решенная ниже:
- Найдите числовое значение многомерного полинома
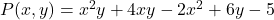
для ценностей
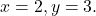
Сначала мы заменяем каждую переменную соответствующим ей значением, т.е. заменяем букву
![]()
на 2 и меняем букву
![]()
на 3:
![]()
Решаем для полномочий:
![]()
Теперь посчитаем продукты:
![]()
И, наконец, делаем сложение и вычитание:
![]()
Таким образом, числовое значение полинома для данных инструкции эквивалентно 41.
Решенные упражнения на числовое значение многочлена
Упражнение 1
Каково числовое значение многочлена P(x) при x=-2?
![]()
Чтобы найти числовое значение многочлена, нам просто нужно подставить значение, данное в операторе, в полиномиальное выражение и решить полученные операции:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
Упражнение 2
Вычислите числовое значение следующего многочлена с дробями для x=4.
![]()
Независимо от того, есть ли у многочлена дроби, процедура нахождения числового значения многочлена всегда одинакова. Поэтому мы должны заменить переменную x на 4 и решить вычисления:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
Упражнение 3
Определить числовое значение многочлена для значений x=3, y=5 и z=-2.
![]()
Для определения численного значения многомерного полинома достаточно подставить данные в задаче значения в алгебраическое выражение и решить полученные операции:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
Упражнение 4
Учитывая полином
![]()
рассчитать значение параметра
![]()
так что
![]()
В этой задаче найти значение неизвестного
![]()
нам нужно решить уравнение
![]()
![]()
Поэтому сначала попытаемся вычислить значение P(-2):
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
Теперь приравняем полученное выражение к 5:
![]()
![]()
И, наконец, решаем полученное уравнение:
![]()
![]()