На этой странице вы узнаете, что такое корни многочлена и как они вычисляются. Кроме того, вы сможете увидеть примеры и упражнения, пошагово решаемые на корнях многочлена.
Каковы корни многочлена?
В математике корни (или нули) многочлена — это значения, сокращающие многочлен. То есть корнями полинома являются все те значения, которые при вычислении в полиноме имеют числовое значение, равное 0.
В конце концов,
![]()
является корнем многочлена
![]()
Ага
![]()
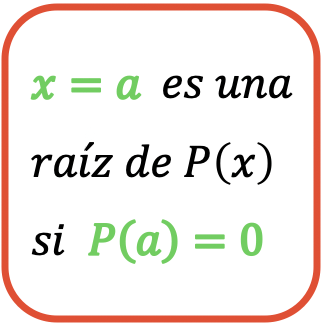
Например, если у нас есть следующий полином:
![]()
Мы можем проверить, что один из корней многочлена равен 1, поскольку числовое значение многочлена при x=1 равно нулю:
![]()
С другой стороны, 3 не является корнем многочлена, потому что это не значение, которое отменяет многочлен, или, другими словами, числовое значение многочлена при x = 3 отличается от нуля:
![]()
Вероятно, теперь вы лучше понимаете, что такое корень многочлена, но разве вам не хотелось бы узнать, сколько корней имеет многочлен? Или как найти все корни многочлена? Что ж, именно это мы и увидим в следующем разделе.
Как вычислить все корни многочлена?
Чтобы найти все корни многочлена, необходимо выполнить следующие действия:
- Сначала вычисляются все делители независимого члена многочлена.
- Во-вторых, все значения, найденные на предыдущем шаге, оцениваются в полиноме.
- Наконец, если при вычислении числа в многочлене его числовое значение равно нулю, указанное число является корнем многочлена. В противном случае указанное число не соответствует корню многочлена.
Эта процедура выводится из теоремы об остатках . Щелкните эту ссылку, чтобы узнать причину использования этой конкретной процедуры.
Пример вычисления корней многочлена
Ниже мы поэтапно решим пример, чтобы вы могли лучше понять, как извлечь корни многочлена.
- Каковы все корни следующего многочлена?
![]()
Прежде всего, мы должны найти делители независимого члена, поскольку каждый корень многочлена также является делителем независимого члена. Итак, делители числа 6:
Делители 6: +1, -1, +2, -2, +3, -3.
Помните, что если число является делителем, то его отрицательное число также является делителем. Так как число делится на положительные и отрицательные числа.
Таким образом, возможные корни или нули многочлена: ±1, ±2, ±3. Поэтому нам необходимо определить числовое значение полинома для всех этих значений. И, для этого, подставим эти значения в выражение многочлена, где есть х:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, полином исчезает только тогда, когда переменная x равна +2 или +3, поэтому вот корни многочлена:
Корни или нули полинома : +2 и +3.
С другой стороны, обратите внимание, что многочлен имеет столько же корней, сколько и его степень, то есть, поскольку многочлен имеет вторую степень, у него два корня. Из свойств корней многочлена (ниже) мы увидим, почему эта характеристика всегда справедлива для любого многочлена.
Мы только что рассмотрели способ нахождения корней многочлена. Однако есть и другие способы добиться этого, например, вы также можете найти корни многочлена с помощью правила Руффини. Нажмите на следующую ссылку, чтобы увидеть примеры правила Руффини. Здесь вы узнаете, из чего состоит этот известный метод, а также каковы различия между двумя процедурами.
Свойства корней многочлена
Корни или нули многочлена имеют следующие характеристики:
- Как мы видели ранее, целые корни (или нули) многочлена являются делителями независимого члена многочлена.
- Если мы знаем все корни многочлена, мы можем выразить этот многочлен в виде произведений биномов типа
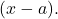
Например, полином
![]()
Имеет 3 корня, которые
![]()
И
![]()
Поэтому мы можем переписать полином в виде трех умножений множителей, каждый из которых образован переменной
![]()
и корень поменял знак:
![Rendered by QuickLaTeX.com \displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce071610927d2723c8ac2e7b299c1c5d_l3.png)
![]()
Это называется полиномиальным факторингом. Фактически, одно из основных применений определения корней многочлена заключается в том, что они используются для его факторизации. По следующей ссылке вы можете узнать, из чего состоит эта особенная операция, а также попрактиковаться с решенными упражнениями на факторизацию полинома .
- Многочлен имеет столько корней, сколько указывает его степень. Таким образом, многочлен второй степени будет иметь 2 корня, многочлен третьей степени — 3 корня, многочлен четвертой степени — 4 корня и так далее.
- Если у многочлена нет независимого члена, это означает, что один из его корней равен 0. Тогда остальные корни должны быть делителями коэффициента монома низшей степени.
Например, следующий полином не имеет независимого члена:
![]()
Таким образом, один корень многочлена обязательно должен быть равен 0. А остальные корни являются делителями коэффициента члена низшей степени, т. е. -2. Точнее, остальные корни
![]()
И
![]()
поэтому все корни многочлена:
Корни или нули полинома: 0, +1 и -2.
- Если корни многочлена не могут быть определены, его называют неприводимым многочленом.
Например, мы попробуем вычислить корни следующего многочлена:
![]()
Единственно возможные корни многочлена — это делители -1, то есть -1 и +1. Поэтому мы оцениваем полином по этим значениям:
![]()
![]()
Ни в коем случае многочлен не сокращается, поэтому он не имеет корней и, следовательно, является неприводимым многочленом.
- Когда многочлен состоит из произведения нескольких многочленов, нет необходимости производить это произведение для вычисления корней, но корни многочлена представляют собой умноженные корни каждого множителя.
Например, если у нас есть следующий полином:
![]()
Из второго свойства корней многочленов мы можем сделать вывод, что корень левого многочлена равен +2, а корень правого многочлена равен -1.
![]()
![]()
Таким образом, корни многочлена, полученные в результате умножения двух множителей, являются соответствующими корнями, т.е. +2 и -1.
![Rendered by QuickLaTeX.com \displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-416399918b5a2a051a6bfc7343ef7960_l3.png)
Решенные упражнения на корни многочленов
Упражнение 1
Определите, если
![]()
является корнем следующего многочлена:
![]()
Чтобы узнать, если
![]()
является корнем полинома, нам нужно оценить его до этого значения. Еще:
![Rendered by QuickLaTeX.com \begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c88c4456693b0c57d55aba68287414c_l3.png)
Числовое значение полинома в
![]()
равно нулю, поэтому фактически является корнем многочлена.
Упражнение 2
Вычислите все корни следующего многочлена:
![]()
Во-первых, чтобы найти возможные корни многочлена, мы должны найти делители независимого члена. Итак, делители числа 2:
Делители 2: +1, -1, +2, -2.
Таким образом, возможные корни или нули многочлена равны ±1 и ±2. Следовательно, нам нужно посчитать, сколько полинома находится во всех этих значениях:
![]()
![]()
![]()
![]()
Таким образом, полином исчезает, когда x равен +1 или +2, поэтому вот корни многочлена:
Корни или нули многочлена : +1 и +2.
Упражнение 3
Найдите корни следующего многочлена:
![]()
Сначала мы должны найти делители независимого члена, поскольку корень многочлена также является делителем независимого члена. Итак, делители числа 4:
Делители 4: +1, -1, +2, -2, +4, -4.
Таким образом, возможные корни или нули многочлена равны ±1, ±2 и ±4. Поэтому мы должны найти числовое значение многочлена во всех этих значениях:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, полином исчезает только тогда, когда x равен +1, +2 или -2, поэтому вот корни многочлена:
Корни или нули полинома : +1, +2 и -2.
Упражнение 4
Найдите корни следующего многочлена:
![]()
В этом случае полином не имеет независимого члена. Следовательно, согласно четвертому свойству корней, объясненному выше, мы знаем, что один из корней многочлена должен быть равен 0.
Корни многочлена:
![]()
Кроме того, в этом случае возможными корнями являются не делители независимого члена, а скорее корни коэффициента члена низшей степени, т. е. 8:
Делители 8: +1, -1, +2, -2, +4, -4, +8, -8.
Таким образом, возможные корни или нули многочлена равны ±1, ±2, ±4 и ±8. Поэтому мы должны вычислить численное значение полинома для всех этих значений:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, полином исчезает, когда x равен +2 или +4, поэтому эти значения являются корнями многочлена. Однако нам также нужно добавить корень 0, который мы нашли в начале задачи. В заключение, все корни многочлена:
Корни или нули многочлена : 0, +2 и +4.
Упражнение 5
Используйте свойства корней многочленов, чтобы вычислить корни следующего многочлена:
![]()
Как мы видели в шестом свойстве корней, когда многочлен образуется произведением множителей, нет необходимости вычислять все корни, поскольку корни всего многочлена являются корнями каждого множителя.
Кроме того, из второго свойства корней многочленов мы можем сделать вывод, что корень первого сомножителя равен +1, а корень второго сомножителя равен -3.
![]()
![]()
Так что нам просто нужно найти корни последнего фактора. Для этого найдем делители независимого члена (-2):
Делители -2: +1, -1, +2, -2.
Таким образом, возможные корни или нули последнего многочлена равны ±1 и ±2. С помощью чего мы должны вычислить числовое значение указанного многочлена во всех этих значениях:
![]()
![]()
![]()
![]()
![]()
Таким образом, корни многочлена справа равны -1 и 2.
Следовательно, корнями всего многочлена являются все найденные корни:
Корни или нули многочлена : +1, -1, +2, -3.