На этой странице вы узнаете, как умножаются многочлены. Вы также сможете увидеть примеры умножения многочленов и, кроме того, пошагово решаемые упражнения. Наконец, вы узнаете, каковы свойства умножения многочленов.

Однако, чтобы полностью понять концепцию умножения многочленов, мы продвинемся от самого простого к самому сложному, то есть начнем с того, как умножить многочлен на число, а затем увидим, как умножить многочлен на число. моном и, наконец, мы объясним, как умножать два или более многочленов вместе.
Советую следовать такому порядку, но если вы считаете, что уже освоили действия с предыдущими многочленами, то можете перейти непосредственно к умножению между многочленами, нажав на индекс:
Умножить многочлен на число
Произведение скаляра (или числа) и многочлена решить довольно просто, достаточно умножить число на коэффициент каждого члена многочлена .
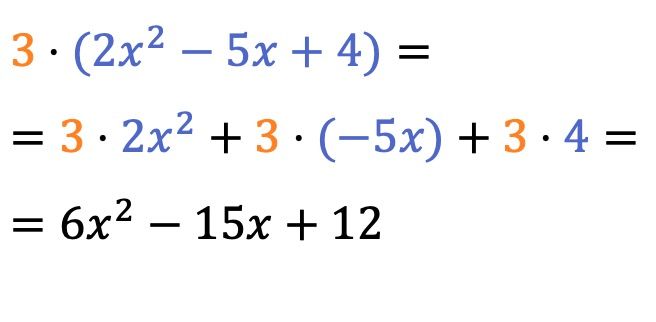
Знак умножения перед круглыми скобками можно опустить.
![Rendered by QuickLaTeX.com \begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-794a3972ecb155b810fc6833caa7d1a1_l3.png)
Умножение многочлена на моном
Прежде чем увидеть, как умножить многочлен на моном, мы сначала вспомним, как мономы умножаются друг на друга, потому что вам нужно знать это, чтобы иметь возможность выполнять этот тип полиномиальной операции.
Произведение двух мономов состоит из умножения их коэффициентов друг на друга и их буквенных частей друг на друга, т. е. умножаются коэффициенты мономов и складываются показатели степеней переменных, имеющих одинаковые основания. Посмотрите на следующий пример:
![]()
Теперь посмотрим, как умножить моном на многочлен:
В математике, чтобы решить задачу умножения монома на многочлен, моном умножается на каждый член многочлена.

Как и раньше, знак умножения можно опустить:
![Rendered by QuickLaTeX.com \begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f3c8bf0b635315032c46506aee223e29_l3.png)
Обратите внимание в предыдущем примере, что при умножении одночленов или многочленов также необходимо учитывать правило знаков. Фактически, очень распространенная ошибка при умножении мономов и многочленов — это неверный знак члена.
Наверняка в какой-то момент, когда вы увидели что-то новое в математике, вы спросили себя: для чего это нужно ? Ну, этот тип умножения используется для получения общего делителя многочлена , операции, которая позволяет упростить многочлены (очень полезно). Посмотреть, что это такое и как рассчитывается общий множитель многочлена, можно по этой ссылке.
Умножение двух многочленов
Как только мы узнаем, как умножать многочлены на числа и на мономы, давайте посмотрим, что это такое и как умножать многочлены на многочлены.
Чтобы умножить многочлены, выполните следующие действия:
- Умножьте каждый член первого многочлена на все члены второго многочлена.
- Сложите (или вычтите) одночлены одной степени (подобные одночлены).
Чтобы вы могли точно понять, что это за метод, мы шаг за шагом решим следующее умножение полиномов:
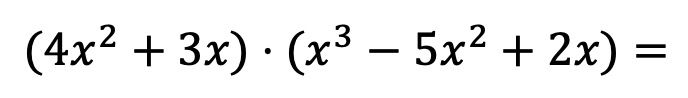
Прежде всего, мы должны умножить каждый элемент первого умножающего многочлена на каждый член второго многочлена:
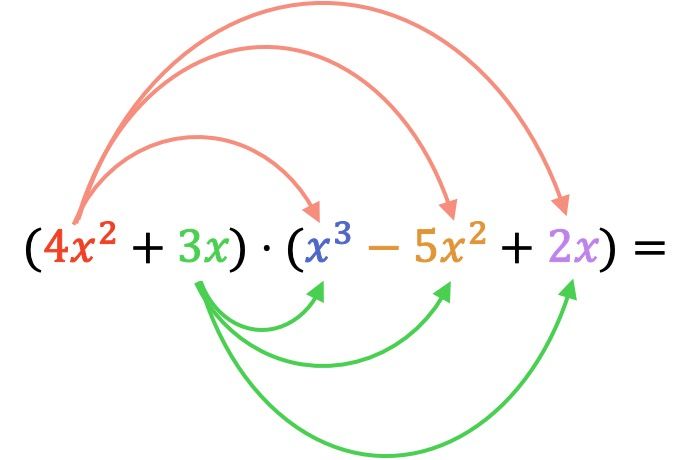
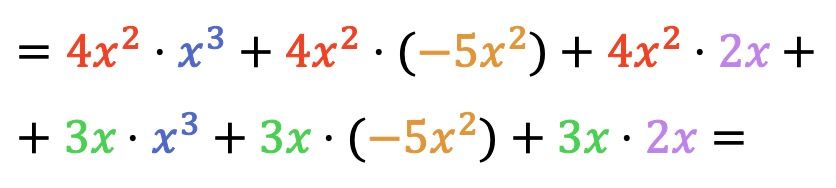
Теперь делаем все умножения одночленов:
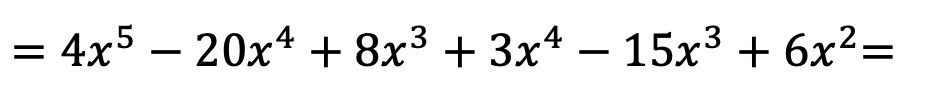
После того, как мы перемножили многочлены, нам просто нужно сгруппировать полученные члены, которые похожи, то есть члены, имеющие одинаковую букву и одинаковый показатель степени:
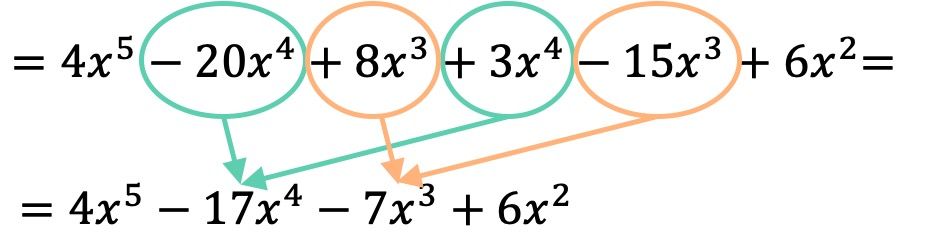
Таким образом, результатом полиномиального умножения будет:
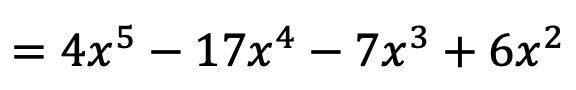
И таким образом мы уже вычислили умножение многочленов. Возможно, сейчас вам это кажется очень трудным, но вы увидите, что, когда вы будете практиковать два-три упражнения, это будет намного легче.
Теперь, когда вы увидели, как решается умножение двух многочленов, вам, вероятно, интересно узнать , как делить многочлены . На самом деле делить многочлены гораздо сложнее, чем их умножать, поэтому мы объяснили процедуру (и советы😉) шаг за шагом, чтобы вы могли ее полностью понять. Если вам интересно, нажмите эту ссылку, чтобы увидеть, как делятся полиномы.
Вертикальное полиномиальное умножение
Мы только что увидели, как умножить многочлен на другой многочлен по горизонтали, но это можно сделать и более классическим способом: умножить многочлены по вертикали. Давайте посмотрим, как этот метод используется, решив пример полиномиального умножения.
Если мы хотим вертикально умножить следующие два многочлена:
![]()
Первое, что нам нужно сделать, это разместить один многочлен ниже другого, как алгебраическое умножение многочленов:
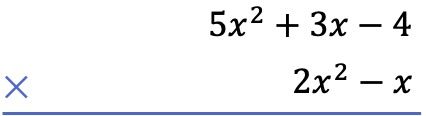
Во-вторых, мы умножаем каждый член приведенного ниже многочлена на каждый член приведенного выше многочлена и размещаем результаты, упорядоченные по столбцам от высшей степени к низшей:
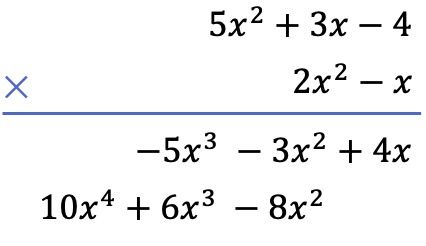
И, наконец, мы добавляем вертикально выровненные термины:
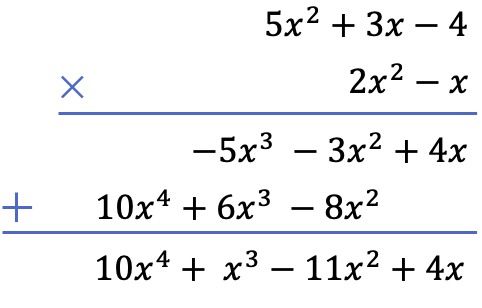
Теперь, когда вы познакомились с двумя существующими методами решения умножения многочленов, знаете ли вы, что вы также можете умножать дроби на многочлены ? И с этими видами дробей можно производить не только умножения, но и всевозможные действия. Нажмите на эту ссылку и узнайте, что такое алгебраические дроби .
Свойства полиномиального умножения
Умножение многочленов имеет следующие характеристики:
- Коммутативное свойство : порядок умножения многочленов не меняет результат умножения.
![]()
- Ассоциативное свойство : при умножении трех или более полиномов результат получается одинаковым независимо от того, как сгруппированы факторы:
![]()
- Распределительное свойство : сумма двух многочленов, умноженная на третий, равна сумме каждого сложения, умноженного на третий многочлен.
![]()
- Степень многочлена , полученного в результате умножения двух многочленов, равна сумме степеней двух перемноженных многочленов.
Решенные упражнения на умножение многочленов
Чтобы вы могли попрактиковаться, я оставляю вам несколько решенных упражнений на умножение многочленов. Вы можете попробовать решить их самостоятельно и сверить свои результаты с предложенным решением. Тогда вы можете задать нам все интересующие вас вопросы в комментариях, мы будем рады вам помочь.
Упражнение 1
Вычислите следующие произведения полиномов и скаляров:
![]()
![]()
![]()
![]()
Чтобы вычислить умножение многочлена на число, необходимо умножить число на коэффициент каждого элемента многочлена. ТАК:
![]()
![]()
![]()
![]()
Упражнение 2
Решите следующие умножения между полиномами и мономами:
![]()
![]()
![]()
![]()
Чтобы решить задачу умножения многочлена на моном, необходимо умножить этот моном на каждый член многочлена. ТАК:
![]()
![]()
![]()
![]()
Упражнение 3
Определите результат следующих умножений многочленов:
![]()
![]()
![]()
Чтобы вычислить умножение двух многочленов, нам нужно умножить каждый элемент первого многочлена на каждый элемент второго многочлена, а затем сгруппировать подобные члены вместе. ТАК:
![Rendered by QuickLaTeX.com \color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-51dbb4634996039c3b67ce506aef648c_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fba45efd14a187f0eaa210f0561c68a4_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32417206d212f4b5ee2a6fb53aa77f30_l3.png)
Упражнение 4
Найдите результат следующих умножений многочленов:
![]()
![]()
![]()
Чтобы вычислить умножение двух многочленов, нам нужно умножить каждый элемент первого многочлена на каждый элемент второго многочлена, а затем добавить аналогичные члены. ТАК:
![Rendered by QuickLaTeX.com \color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ba837feab91328dd1ac60093307a3691_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-486aedf31fca13fd2b4af2c72a3b34a1_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81d28b9e6595a4e28d09d46bab74c467_l3.png)
Упражнение 5
Вычислите следующие умножения многочленов:
![]()
![]()
![]()
Чтобы составить произведение 2-х многочленов, необходимо каждый член первого многочлена умножить на каждый член второго многочлена, а затем сгруппировать полученные подобные мономы. Еще:
![Rendered by QuickLaTeX.com \color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d6d4bb6d12ab30b22cbb7cffc071093c_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-efacae5cc2c79ff47d4bca96ab082eb7_l3.png)
![Rendered by QuickLaTeX.com \color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2b27ccbbd6344d296250e7dc9f3fbbbf_l3.png)
Упражнение 6
Решите следующее умножение трех многочленов:
![]()
Работа задачи состоит из 2-х умножений многочленов, точнее состоит из двух биномов и трёхчлена. Поэтому нам нужно сначала найти произведение, а затем умножить результат на оставшийся полином.
Поэтому мы вычисляем первое умножение:
![Rendered by QuickLaTeX.com \begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9860e611d9fee24111ec42d5451366f_l3.png)
А теперь решаем оставшееся умножение:
![Rendered by QuickLaTeX.com \begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a4280995c52ffc8cd833b76b72584c96_l3.png)
Упражнение 7
Умножьте следующие многочлены на рациональные коэффициенты (с дробями):
![]()
Хотя у многочленов есть дроби, это все равно умножение двух многочленов. Поэтому его необходимо решать, как любое полиномиальное произведение: перемножить все элементы вместе, а затем сгруппировать подобные мономы.
Поэтому мы умножаем многочлены:
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e144cee08d9d9a02af24c2338c5d37c_l3.png)
И, наконец, добавляем (или вычитаем) термины, буквальные части которых совпадают:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-54b9cfbdee75b2c0d95499f25b6547ec_l3.png)
Для успешного выполнения этого упражнения важно было освоить операции с дробями. Но если у вас возникнут вопросы по какому-либо шагу, вы можете задать их в комментариях и мы ответим на них максимально быстро.