На этой странице мы объясняем, как выполнять все операции с одночленами (сложение, вычитание, умножение, деление и степень). Кроме того, вы сможете увидеть примеры каждого вида действий с одночленами и потренироваться на пошагово решаемых упражнениях.
Сложение и вычитание одночленов
Два или более монома можно складывать или вычитать только в том случае, если они являются подобными мономами, то есть если два монома имеют одинаковую литеральную часть (те же буквы и одинаковые показатели степени).
Тогда сумма (или вычитание) двух подобных одночленов равна другому одночлену, составленному из той же буквальной части и суммы (или вычитания) коэффициентов этих двух одночленов.


Сложение и вычитание одночленов также называют сложением и вычитанием одночленов соответственно.
Примеры сложения и вычитания одночленов
Чтобы вы могли наглядно понять, как складывать и вычитать два и более одночленов, оставляем вам ниже несколько примеров:
Мономы в последнем примере нельзя складывать или вычитать, поскольку они не похожи или, другими словами, имеют разные неизвестные или показатели степени.
Произведение нескольких одночленов
Чтобы решить произведение одночлена на число, просто умножьте коэффициент одночлена на это число, оставив буквальную часть одночлена прежней.
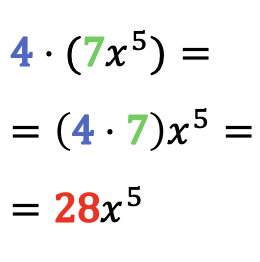
Примеры умножения чисел на одночлены
Умножение одночленов
Результатом умножения двух мономов является другой моном, коэффициент которого является произведением коэффициентов мономов и буквенная часть которого получается умножением переменных, имеющих одинаковую основу, то есть сложением их показателей.

Следовательно, чтобы перемножить два разных монома, мы должны перемножить коэффициенты между ними и сложить показатели степеней, имеющих одинаковое основание.
Однако если мы перемножим два монома с разной базовой степенью , нам просто нужно перемножить их коэффициенты вместе и оставить степени одинаковыми. Например:
![]()
С другой стороны, при умножении одночленов необходимо учитывать правило знаков:
- Положительный моном, умноженный на положительный моном, дает другой положительный моном.
- Положительный моном, умноженный на отрицательный моном (или наоборот), равен отрицательному моному.
- Два отрицательных монома, перемноженные вместе, дают положительный моном.
Примеры мономиальных умножений
Ниже приведены несколько примеров умножения одночленов, чтобы вы могли увидеть, как это делается:
Как вы видели, решить задачу умножения одночленов относительно просто. Но следует иметь в виду, что одночлены также можно умножать на многочлены, причем даже 2 и более многочленов можно умножать вместе. Если вам больше интересно, вы можете увидеть, как работают все эти операции, нажав на полиномиальное умножение .
Деление одночленов
В математике результатом деления одночленов является другой моном, коэффициент которого эквивалентен частному коэффициентов мономов и буквальная часть которого получается путем деления переменных, имеющих одно и то же основание, то есть путем вычитания их показателей. .

Очевидно, любое деление одночленов можно выразить и дробью:
![]()
Как и при умножении, при делении одночленов необходимо применять закон знаков:
- Положительный моном, разделенный на положительный моном, дает еще один положительный моном.
- Положительный моном, разделенный на отрицательный моном (или наоборот), эквивалентен отрицательному моному.
- Два отрицательных монома, разделенные друг на друга, дают положительный моном.
Примеры деления одночленов
Ниже вы можете увидеть больше примеров того, как делятся два или более одночленов:
Наверняка в какой-то момент, когда вы узнавали что-то новое в математике, вы задавались вопросом: для чего это нужно ? Ну, мономиальное деление используется для деления многочленов. На самом деле, довольно часто допускаются ошибки при делении многочленов, потому что два монома были разделены неправильно. Именно поэтому мы рекомендуем теперь, когда вы знакомы с делением между одночленами, посмотреть, как рассчитывается деление многочленов , ведь теперь вам будет гораздо проще освоить эту процедуру (она довольно сложная).
Степень монома
В математике, чтобы вычислить степень монома, каждый элемент монома возводится в показатель степени . Другими словами, степень монома состоит из возведения его коэффициента и его переменных (букв) в показатель степени.

Помните из свойств степеней, что при возведении и без того большого члена показатели степени умножаются. Вот почему в степени монома показатель каждой буквы всегда умножается на показатель, указывающий степень .
С другой стороны, чтобы правильно провести эту операцию, необходимо помнить следующее свойство полномочий:
- Отрицательный моном, возведенный в четную степень, эквивалентен положительному моному.
- Вместо этого отрицательный моном, возведенный в нечетную степень, приводит к отрицательному моному.
Примеры степеней одночленов
Мы оставляем вам несколько примеров, чтобы вы могли ясно понять, как вычисляется степень монома:
Операции, совмещенные с одночленами
Увидев, что представляют собой все действия с одночленами, знайте, что их также можно комбинировать друг с другом. То есть мы можем найти упражнения, в которых нас просят решить действия с одночленами, где задействованы все виды: сложение, вычитание, умножение, деление и степени.
Но не волнуйтесь, они не так сложны, как кажутся. Единственное, что вам нужно запомнить, это порядок разрешения комбинированных операций:
- Сначала решаются операции с одночленами в скобках.
- Затем вычисляются степени мономов.
- В-третьих, выполняются умножение и деление одночленов.
- И, наконец, определяются сложение и вычитание одночленов.
Я уверен, что решив пример, вы увидите это более наглядно:
Пример совместной работы одночленов
![]()
Прежде всего нам необходимо решить действия с одночленами в скобках:
![]()
В этом случае у нас нет сил. Итак, теперь давайте посчитаем умножение и деление одночленов:
![]()
И, наконец, складываем и вычитаем одночлены:
![]()
![]()
Решенные упражнения на действия с одночленами.
Если вы хотите попрактиковаться, мы оставляем вам ниже несколько упражнений, решенных шаг за шагом сложности ESO, по операциям с одночленами.
Упражнение 1
Вычислите следующие операции сложения и вычитания одночленов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Упражнение 2
Решите следующие умножения одночленов:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![\text{F)} \ 7x^3y^2 \cdot 5x^8z^4 \cdot (-2x^2y^5z^3)= <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-bb20ebb96e0dff759d07813f6fff9470_l3.png" height="22" width="195" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[35x^{11}y^2z^4\cdot (-2x^2y^5z^3) =\]" title="Rendered by QuickLaTeX.com"/> \bm{-70x^{13}y^7z^7}» title=»Rendered by QuickLaTeX.com»></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-d92004db2f9cc2fc28f7b5358dcb5932_l3.png)
![\text{F)} \ 48x^8y^6z^{10} : (-6x^4y^{2}z^4) : (-4x^2y^2z^3)=<span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-6dc0e068dbf84cef6abfe7e1789d245b_l3.png" height="22" width="194" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[-8x^4y^4z^6: (-4x^2y^2z^3)=\]" title="Rendered by QuickLaTeX.com"/> \bm{2x^2y^2z^3}» title=»Rendered by QuickLaTeX.com»></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b1554d59ad6a39e24db564712789ee7_l3.png)