В этой статье мы увидим , как представить любой тип функции на графике. Кроме того, вы найдете решенные пошаговые упражнения по представлению функций на графике.
Как представить функцию на графике
Для представления функции на графике необходимо выполнить следующие действия:
- Найдите область определения функции.
- Рассчитайте точки среза функции с помощью декартовых осей.
- Вычислите асимптоты функции.
- Изучите монотонность функции и найдите ее относительные экстремумы .
- Изучите кривизну функции и найдите ее точки перегиба .
- Постройте точки отсечки, асимптоты, относительные экстремумы и точки перегиба, а затем постройте функцию.
Пример представления функции
Чтобы вы могли увидеть, как функция представляется графически, поэтапно решим следующее упражнение:
- Постройте на графике следующую рациональную функцию:
![]()
Первое, что нужно сделать, это вычислить область определения функции . Это рациональная функция, поэтому нам нужно приравнять знаменатель нулю, чтобы увидеть, какие числа не принадлежат области определения функции:
![]()
![]()
Итак, когда x равен 1, знаменатель будет равен 0, и, следовательно, функция не будет существовать. Таким образом, область определения функции состоит из всех действительных чисел, кроме x=1.
![]()
Чтобы найти точку пересечения с осью X , надо решить уравнение
![]()
Поскольку функция всегда имеет значение 0 по оси X:
![]()
![]()
Термин
![]()
Это предполагает деление всей левой части, чтобы мы могли умножить ее на всю правую часть:
![]()
![]()
![]()
Таким образом, точка пересечения с осью OX равна:
![]()
И чтобы найти точку пересечения с осью Y , вычисляем
![]()
Поскольку x всегда равен 0 по оси Y:
![]()
Следовательно, точка отсечения по оси OY равна:
![]()
В этом случае при прохождении функции через начало координат точка пересечения с осью X совпадает с точкой пересечения с осью Y.
Как только мы узнаем область определения и точки отсечения, нам нужно вычислить асимптоты функции .
Чтобы узнать, имеет ли функция вертикальные асимптоты, нам нужно вычислить предел функции в точках, не принадлежащих области определения (в данном случае x=1). А если результат бесконечен, то это вертикальная асимптота. Еще:
![]()
Поскольку предел функции, когда x стремится к 1, дает бесконечность, x=1 является вертикальной асимптотой:
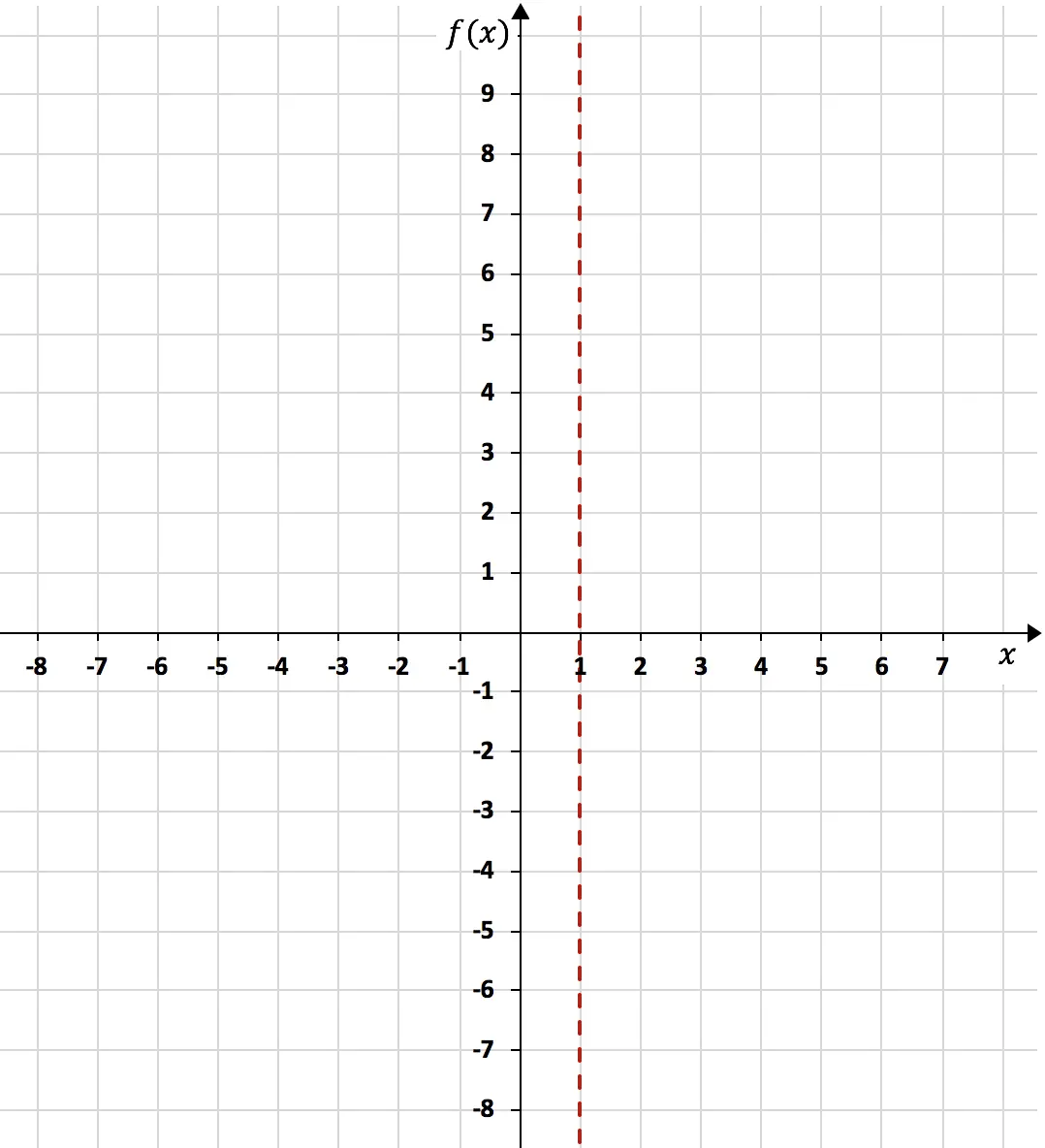
После того как вертикальная асимптота рассчитана, необходимо вычислить боковые пределы функции по ней. Поскольку мы не знаем, будет ли функция стремиться к -∞ или +∞ при приближении к x=1 слева, и мы не знаем, когда она приближается к x=1 справа.
Таким образом, приступим к вычислению левого бокового предела функции при x=1:
![]()
Чтобы численно рассчитать боковую границу в точке, необходимо подставить в функцию число, находящееся очень близко к точке. В данном случае нам нужно число, очень близкое к 1 слева, например 0,9. Поэтому мы подставляем точку 0,9 в функцию:
![]()
Боковые пределы асимптоты могут давать только +∞ или -∞. А поскольку, подставив слева в функцию число, очень близкое к 1, мы получили отрицательный результат, то предел слева равен -∞:
![]()
Теперь проделаем ту же процедуру с правой границей:
![]()
Подставляем в функцию число, очень близкое к 1 справа. Например пункт 1.1:
![]()
В этом случае результат бокового предела является положительным числом. Таким образом, предел справа равен +∞:
![]()
В заключение, при x=1 функция стремится к минус бесконечности слева и к плюс бесконечности справа:
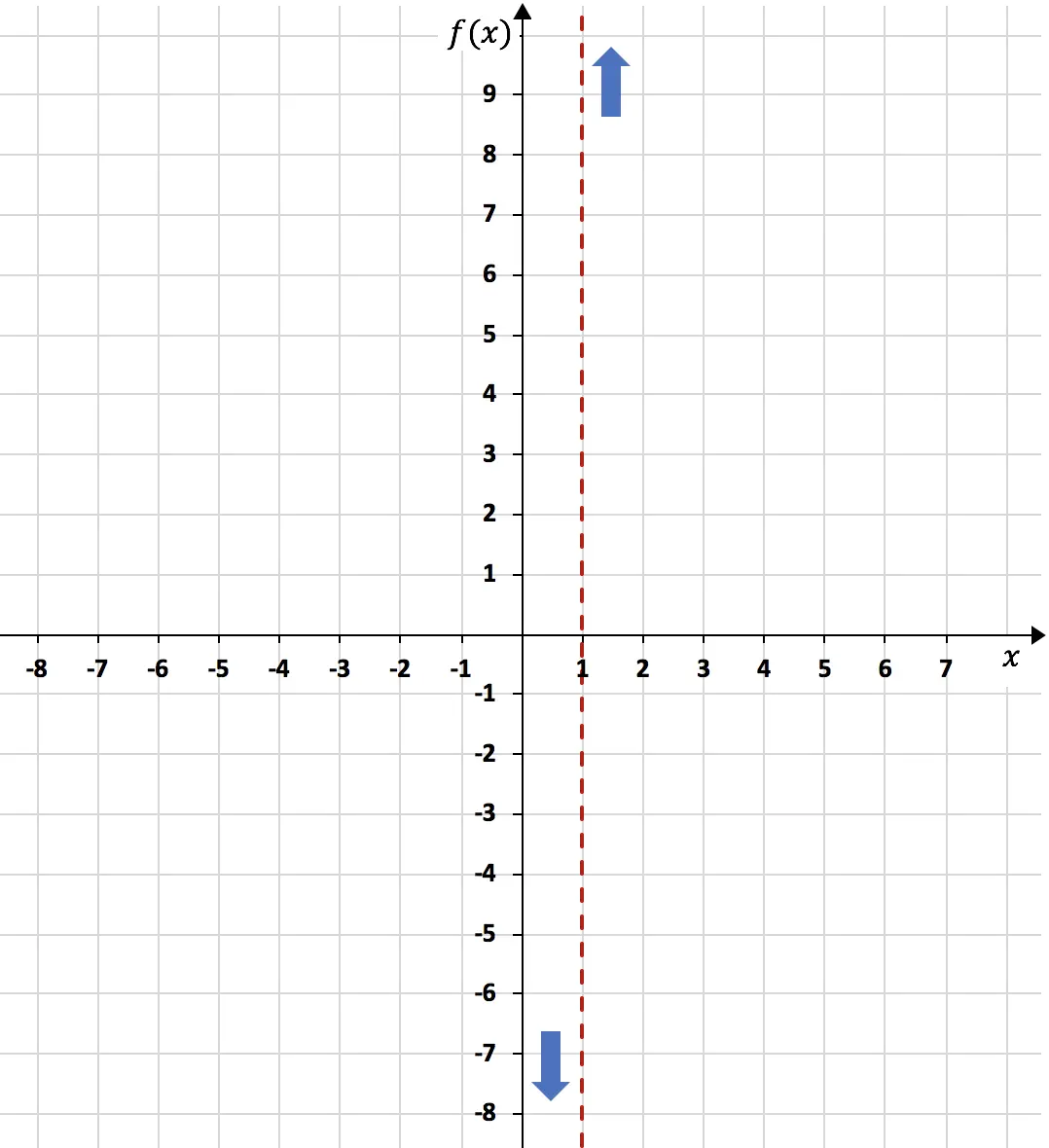
С другой стороны, горизонтальная асимптота функции будет результатом бесконечного предела функции. Еще:
![]()
Вспомните , как вычислять бесконечные пределы рациональных функций:
![\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.» title=»Rendered by QuickLaTeX.com» height=»139″ width=»767″ style=»vertical-align: 0px;»></p>
</p>
</div>
<p> Бесконечный предел функции дал нам +∞, поэтому у функции нет горизонтальной асимптоты.</p>
<p> Теперь вычислим наклонную асимптоту. Наклонные асимптоты имеют вид</p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-2c969e4b99985b44006e57d554ff0247_l3.png)
![]()
. И
![]()
Он рассчитывается по следующей формуле:
![]()
![]()
x такой, как если бы в знаменателе была 1:
![]()
Это деление дробей, поэтому умножаем их поперечно:
![]()
![]()
И вычисляем лимит:
![]()
Итак, м=1. Теперь мы вычисляем
![]()
по следующей формуле:
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty](https://mathority.org/wp-content/ql-cache/quicklatex.com-10dfa8fdcfbf0c978e02374654a66b7d_l3.png)
Но мы получаем неопределенность бесконечность минус бесконечность, поэтому нам придется привести слагаемые к общему знаменателю. Для этого умножим и разделим слагаемое х на знаменатель дроби:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-70026c2aed1bb58a120f8c18423d9ef5_l3.png)
Теперь, когда эти два термина имеют одинаковый знаменатель, мы можем сгруппировать их:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-7702287a02af6d8e3dddaa3f0c6eb1b5_l3.png)
И, наконец, решаем предел:
![Rendered by QuickLaTeX.com \displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1](https://mathority.org/wp-content/ql-cache/quicklatex.com-feb5faa9dc5d3b68d3273ad4d75d2bb1_l3.png)
Итак, n = 1. Следовательно, наклонная асимптота:
![]()
![]()
![]()
После того как мы вычислили наклонную асимптоту, представим ее на том же графике, составив таблицу значений:
![]()

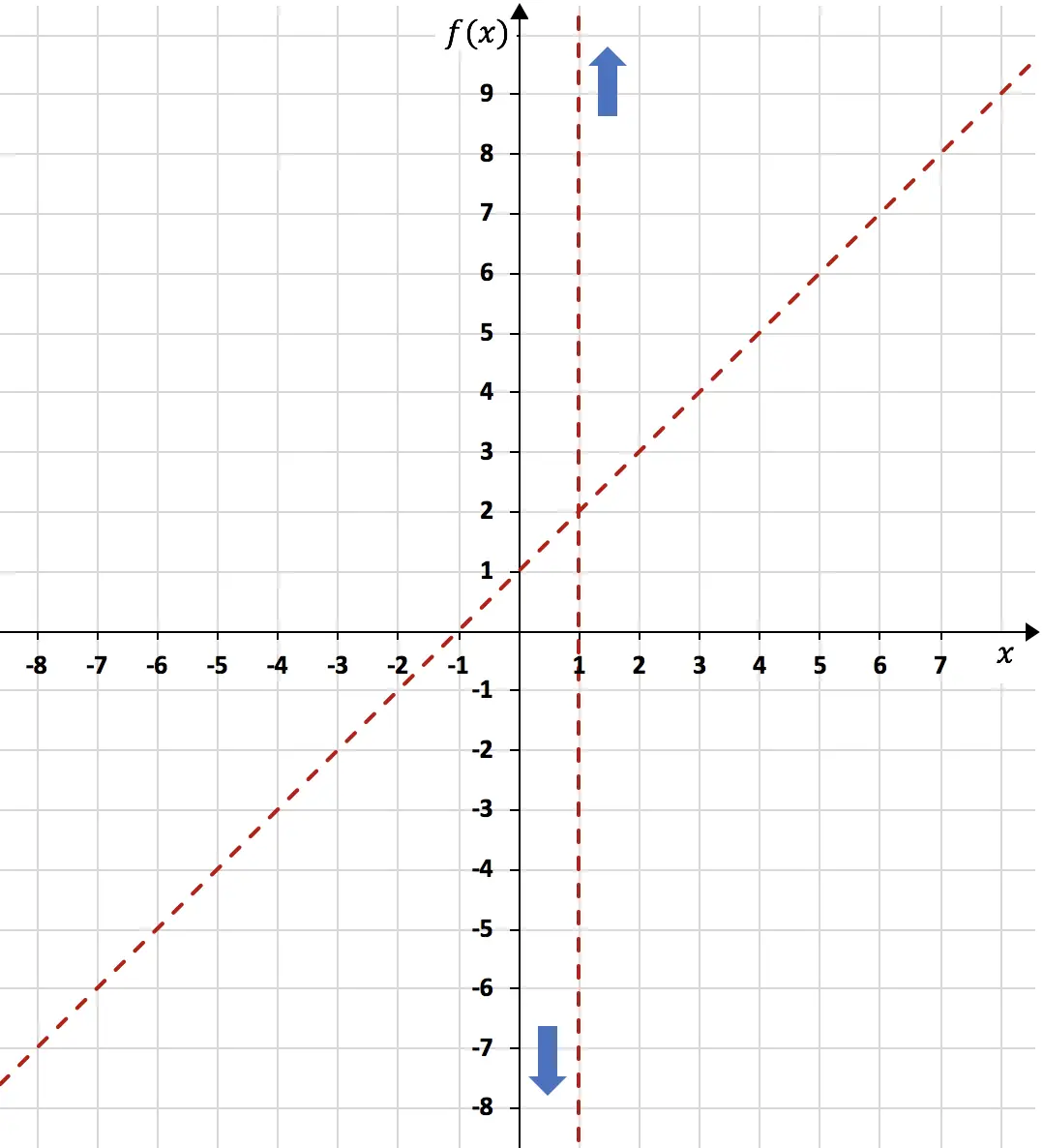
Теперь, когда мы знаем все асимптоты функции, нам нужно проанализировать монотонность функции . То есть нам необходимо изучить, в каких интервалах функция возрастает, а в каких – убывает. Поэтому мы вычисляем первую производную функции:
![]()
![]()
А теперь приравняем производную к 0 и решим уравнение:
![]()
![]()
Термин
![]()
Это предполагает деление всей левой части, чтобы мы могли умножить ее на всю правую часть:
![]()
![]()
Выделим общий множитель для решения квадратного уравнения:
![]()
Чтобы умножение было равно 0, один из двух элементов умножения должен быть нулем. Поэтому положим каждый множитель равным 0 и получим оба решения уравнения:
![Rendered by QuickLaTeX.com \displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-55127e675ce8f7742db17d565c2ae507_l3.png)
Теперь мы представляем на числовой прямой все найденные критические точки, то есть точки, которые не принадлежат области определения (x=1) и те, которые сокращают производную (x=0 и x=2):

И мы оцениваем знак производной в каждом интервале, чтобы узнать, увеличивается или уменьшается функция. Поэтому мы берем точку в каждом интервале (никогда не критические точки) и смотрим, какой знак имеет производная в этой точке:
![]()
![]()
![]()
![]()
![]()
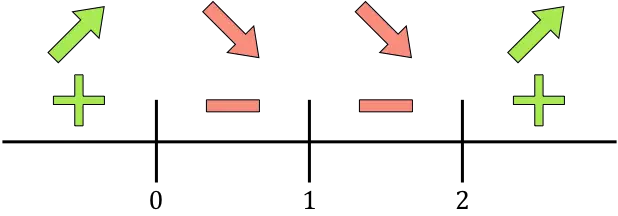
Если производная положительна, это означает, что функция возрастает, а если производная отрицательна, это означает, что функция убывает. Следовательно, интервалы роста и падения составляют:
Рост:
![]()
Снижаться:
![]()
Кроме того, при x=0 функция переходит от возрастания к убыванию, поэтому x=0 является относительным максимумом функции. А при x=2 функция переходит от убывания к увеличению, поэтому x=2 является относительным минимумом функции.
Наконец, подставляем найденные экстремумы в исходную функцию, чтобы найти координату Y точек:
![]()
![]()
Таким образом, относительные экстремумы функции таковы:
Максимум в точку
![]()
Минимум для точки
![]()
Представляем на графике максимум и минимум:
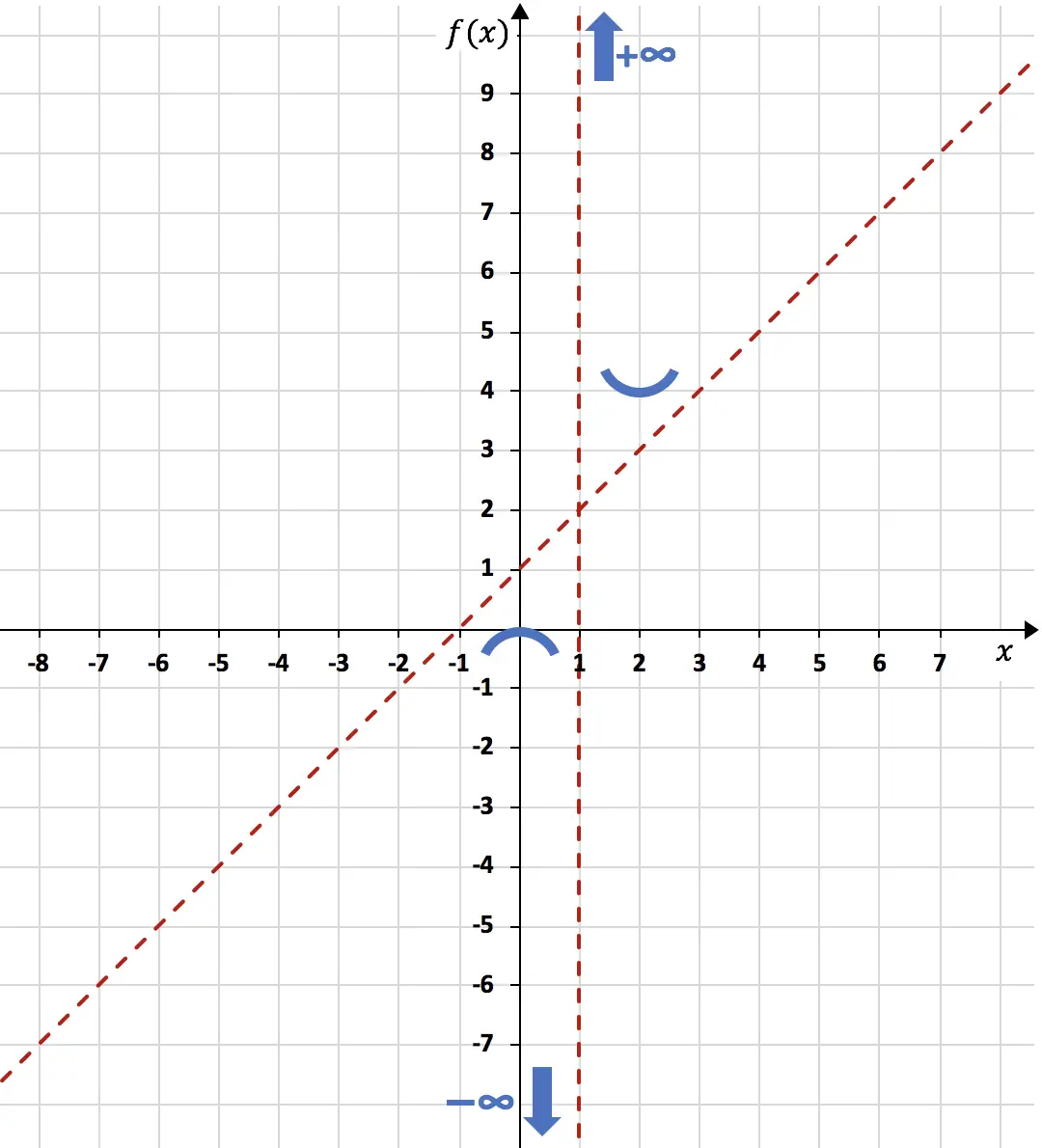
Наконец, достаточно изучить кривизну функции , то есть изучить интервалы вогнутости и выпуклости функции. Для этого вычислим его вторую производную:
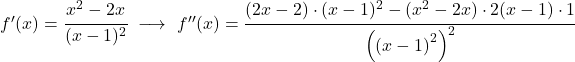
![]()
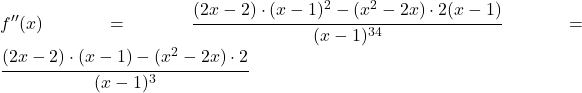
![]()
![]()
А теперь приравняем вторую производную нулю и решим уравнение:
![]()
![]()
![]()
![]()
2 никогда не будет равно 0, поэтому уравнение
![]()
Решения нет.
Теперь мы представляем на числовой прямой все найденные критические точки, то есть точки, которые не принадлежат области определения (x=1) и те, которые сокращают вторую производную (в данном случае их нет):

И мы оцениваем знак производной в каждом интервале, чтобы узнать, является ли функция выпуклой или вогнутой. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет производная в этой точке:
![]()
![]()
![]()

И, наконец, выводим интервалы вогнутости и выпуклости функции. Если вторая производная положительна, это означает, что функция выпуклая.
![]()
, и если вторая производная отрицательна, это означает, что функция вогнутая
![]()
. Следовательно, интервалы вогнутости и выпуклости равны:
Выпуклый
![]()
:
![]()
Вогнутый
![]()
:
![]()
Однако, хотя при x=1 и происходит изменение кривизны, это не точка перегиба. Потому что x=1 не принадлежит области определения функции.
Итак, мы можем завершить представление функции, используя все, что мы вычислили:
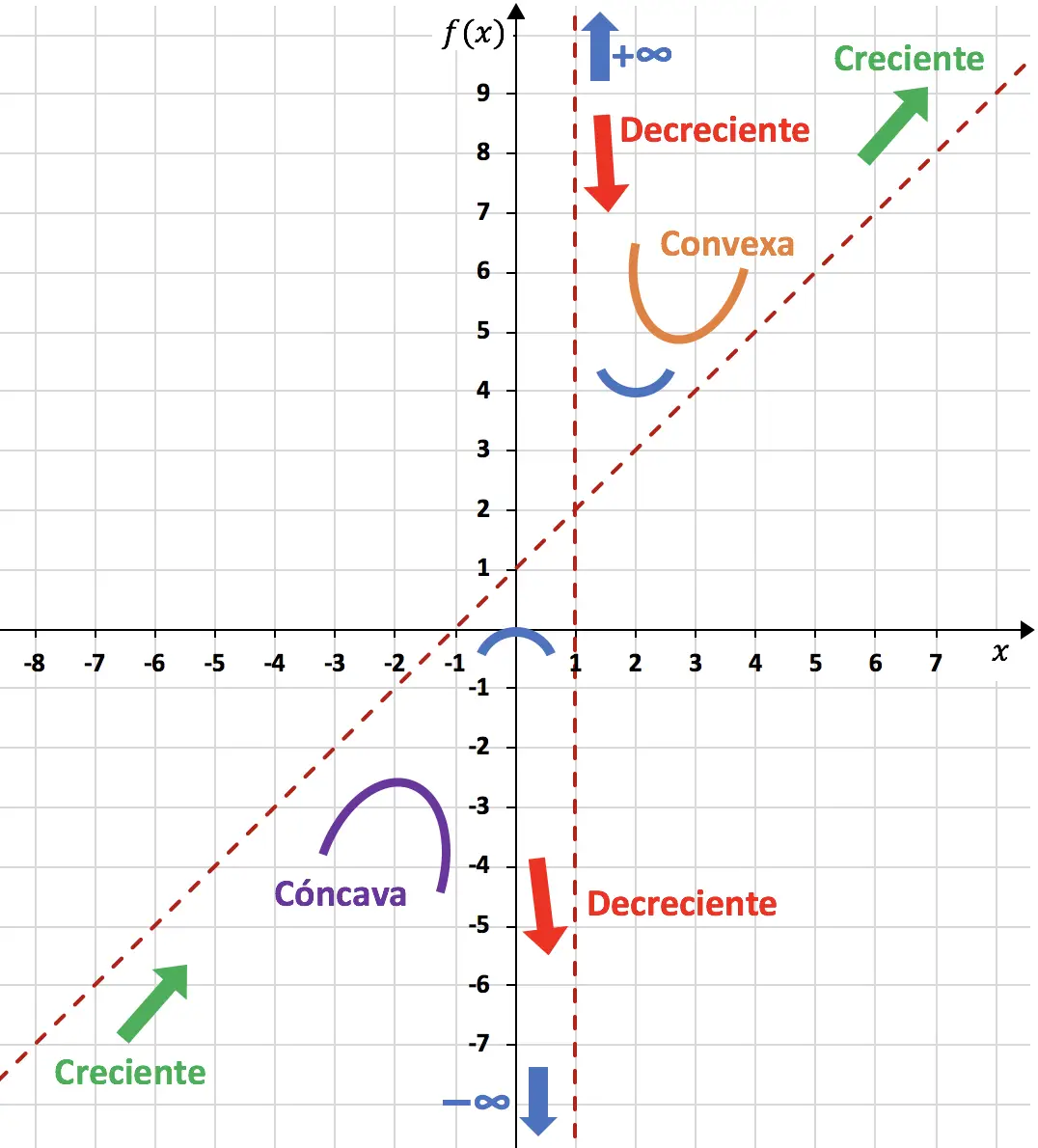
Таким образом, функция, представленная на графике, выглядит следующим образом:
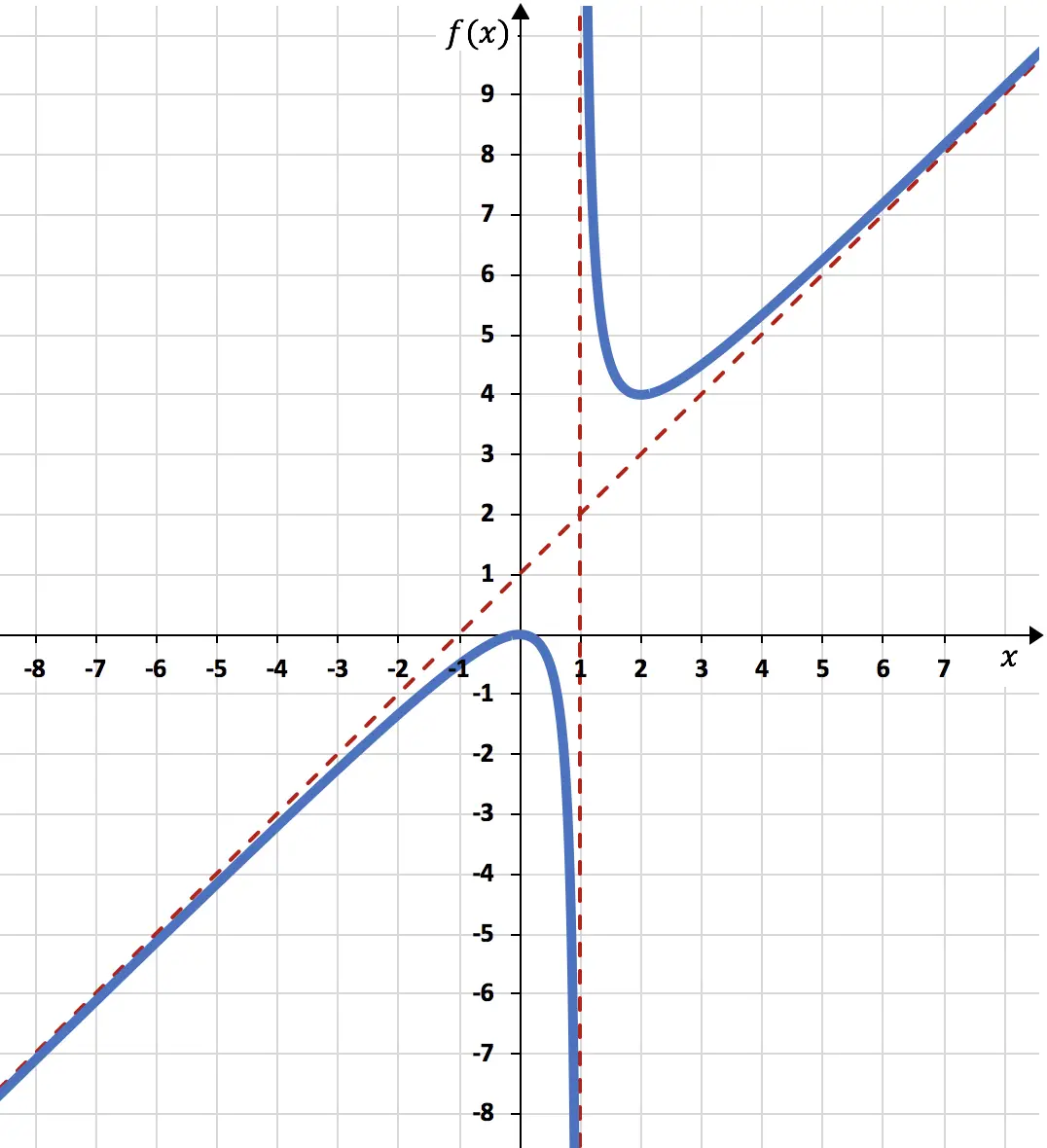
Решенные упражнения на представление функций
Упражнение 1
Постройте график следующей полиномиальной функции:
![]()
Первое, что нужно сделать, это вычислить область определения функции. Это полиномиальная функция, поэтому область определения состоит только из действительных чисел:
![]()
Чтобы найти точку пересечения с осью X, решаем
![]()
![]()
![]()
Это уравнение степени больше 2. Поэтому факторизуем уравнение:
![]()
Итак, x=-1 — это решение. А остальные решения вычисляем, решив полученное квадратное уравнение:
![Rendered by QuickLaTeX.com \begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e79a2a2f6650c4095c0dca52188c40c3_l3.png)
Таким образом, точками пересечения с осью X являются:
![]()
И
![]()
И чтобы найти точку пересечения с осью Y, вычисляем
![]()
Поскольку x всегда равен 0 по оси Y:
![]()
Таким образом, точка пересечения с осью Y равна:
![]()
Чтобы узнать, имеет ли функция вертикальные асимптоты, нам нужно вычислить предел функции в точках, не принадлежащих области определения. В этом случае в домен входят все действительные числа. Таким образом, функция не имеет вертикальной асимптоты.
С другой стороны, горизонтальная асимптота функции будет результатом бесконечного предела функции. Еще:
![]()
Бесконечный предел функции дал нам +∞, поэтому у функции нет горизонтальной асимптоты.
Теперь вычислим наклонную асимптоту. Наклонные асимптоты имеют вид
![]()
И
![]()
Он рассчитывается по следующей формуле:
![]()
![]()
Предел дал нам +∞, поэтому функция также не имеет наклонной асимптоты.
Чтобы изучить монотонность функции, необходимо сначала вычислить ее производную:
![]()
Теперь приравняем производную к 0 и решим уравнение:
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d23e2b378508baca9f51117fc8767e90_l3.png)
Теперь мы представим на числовой прямой все полученные особые точки, то есть точки, которые не принадлежат области определения (в данном случае они все принадлежат), и те, которые сокращают производную (x = 0 и x = 2). :

И мы оцениваем знак производной в каждом интервале, чтобы узнать, увеличивается или уменьшается функция. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет производная в этой точке:
![]()
![]()
![]()

Если производная положительна, это означает, что функция возрастает, а если производная отрицательна, это означает, что функция убывает. Следовательно, интервалы роста и падения составляют:
Рост:
![]()
Снижаться:
![]()
Функция переходит от возрастания к убыванию при x=0, поэтому x=0 является максимумом функции. И функция переходит от убывания к увеличению при x=2, поэтому x=2 является минимумом функции.
Наконец, подставляем найденные экстремумы в исходную функцию, чтобы найти координаты Y точек:
![]()
![]()
Таким образом, относительные экстремумы функции таковы:
Максимум в точку
![]()
Минимум для точки
![]()
Для изучения кривизны функции вычислим ее вторую производную:
![]()
Теперь приравняем вторую производную к 0 и решим уравнение:
![]()
![]()
![]()
![]()
Изобразим на прямой все найденные особые точки, то есть точки, не принадлежащие области определения (в данном случае все они принадлежат), и те, которые сокращают производную (x=1):

А теперь мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет вторая производная в этой точке:
![]()
![]()

Если вторая производная положительна, это означает, что функция выпуклая.
![]()
, и если вторая производная отрицательна, это означает, что функция вогнутая
![]()
. Следовательно, интервалы вогнутости и выпуклости равны:
Выпуклый
![]()
:
![]()
Вогнутый
![]()
:
![]()
Кроме того, функция меняется с вогнутой на выпуклую при x=1, поэтому x=1 является точкой перегиба функции.
Наконец, подставляем найденные точки перегиба в исходную функцию, чтобы найти координату Y точек:
![]()
Таким образом, поворотными моментами функции являются:
Поворотные моменты:
![]()
Наконец, на основе всей рассчитанной нами информации построим график функции:
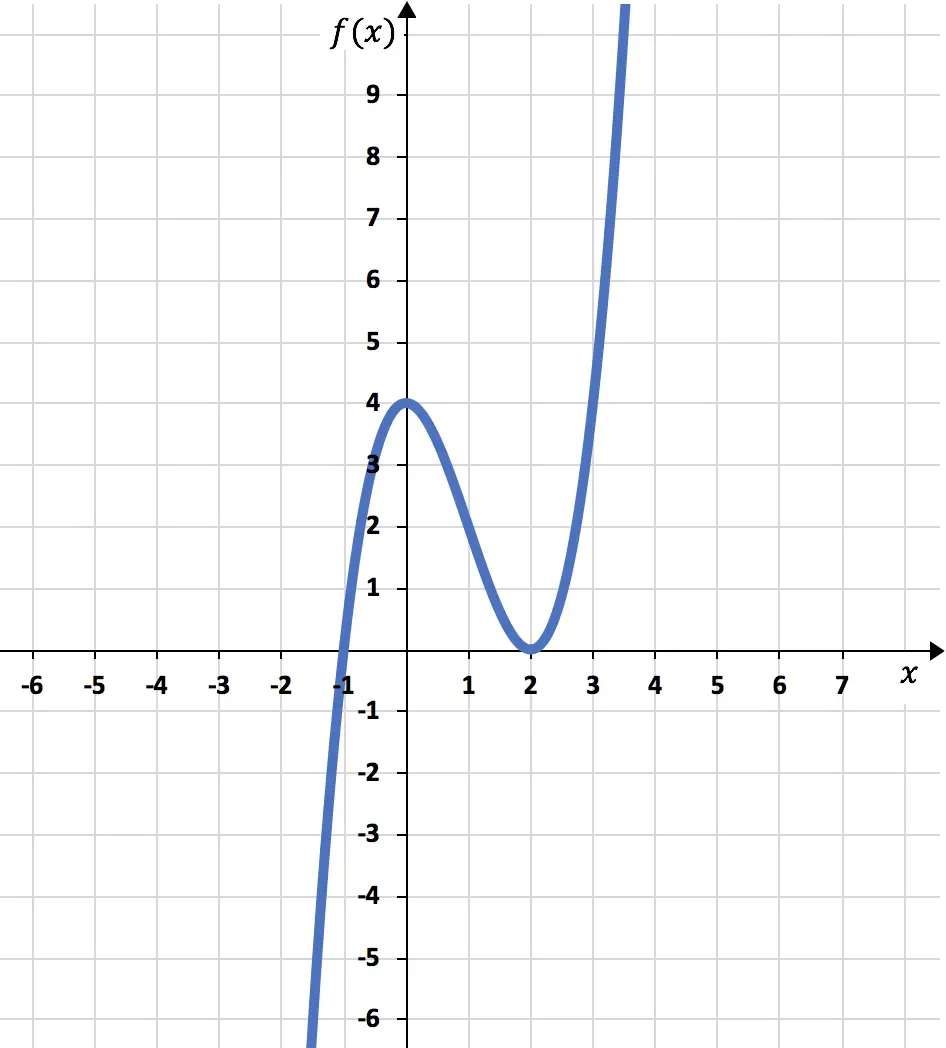
Упражнение 2
Постройте график следующей рациональной функции:
![]()
Чтобы найти область определения функции, приравняем знаменатель. приравняем дробь к нулю и решим полученное уравнение:
![]()
![]()
![]()
![]()
![]()
Во-вторых, мы определяем пороги функции с осью x, равной алгебраическому выражению функции. сталь:
![]()
![]()
![]()
![]()
![]()
![]()
Из отрицательного числа не существует квадратного корня. Следовательно, функция не пересекает ось X.
И чтобы найти точку пересечения с осью компьютера, оцениваем функцию при x=0.
![]()
Таким образом, точка пересечения с осью Y равна:
![]()
Чтобы узнать, имеет ли функция вертикальные асимптоты, нам нужно вычислить предел функции в точках, не принадлежащих области определения (в данном случае x=-1 и x=+1). А если результат бесконечен, то это вертикальная асимптота. Еще:
![]()
Поскольку предел функции при приближении x к -1 дает бесконечность, x=-1 является вертикальной асимптотой.
Вычислим боковые пределы асимптоты x=-1, подставив в функцию очень близкое к ней число:
![]()
![]()
Теперь посмотрим, является ли x=+1 вертикальной асимптотой:
![]()
Поскольку предел функции при приближении x к +1 дает бесконечность, x=+1 является вертикальной асимптотой.
Вычислим боковые пределы асимптоты x=1, подставив в функцию очень близкое к ней число:
![]()
![]()
С другой стороны, горизонтальная асимптота функции будет результатом бесконечного предела функции. Еще:
![]()
Бесконечный предел функции дал нам 1, поэтому функция имеет горизонтальную асимптоту при y=1.
Поскольку функция имеет горизонтальную асимптоту, наклонной асимптоты у нее не будет.
Продифференцируем функцию, затем исследуем интервалы роста и убывания:
![]()
![]()
Теперь приравняем производную к 0 и решим уравнение:
![]()
![]()
![]()
![]()
![]()
Мы представляем на линии все рассчитанные критические точки: точки, не принадлежащие области определения (x=-1 и x=+1), а также точки, которые сокращают производную (x=0):

И мы оцениваем знак производной в каждом интервале, чтобы узнать, увеличивается или уменьшается функция. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет производная в этой точке:
![]()
![]()
![]()
![]()
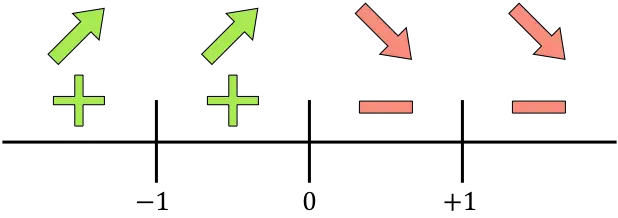
Функция возрастает там, где производная положительна, и убывает там, где функция отрицательна:
Рост:
![]()
Снижаться:
![]()
Функция переходит от возрастания к убыванию при x=0, поэтому x=0 является локальным максимумом функции.
Подставим найденный экстремум в исходную функцию, чтобы найти координату Y точки:
![]()
Таким образом, относительные экстремумы функции таковы:
Максимум в точку
![]()
Для изучения кривизны функции вычислим ее вторую производную:
![f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}» title=»Rendered by QuickLaTeX.com»></p>
</p>
<p class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-802852beb818dd5a0dce2f30374f3a88_l3.png) Все термины имеют
Все термины имеют
![]()
, поэтому мы можем упростить дробь:
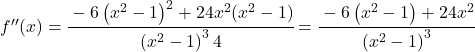
![]()
Теперь приравняем вторую производную к 0 и решим уравнение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Из отрицательного числа не существует квадратного корня. Таким образом, нет точки, которая соответствует
![]()
Теперь изобразим на прямой все найденные особые точки, то есть точки, не принадлежащие области определения (x=-1 и x=+1) и те, которые сокращают вторую производную (в данном случае не существует любой):
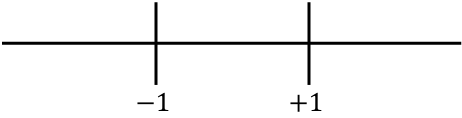
И мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет вторая производная в этой точке:
![]()
![]()
![]()

Если вторая производная положительна, это означает, что функция выпуклая.
![]()
, и если вторая производная отрицательна, это означает, что функция вогнутая
![]()
. Следовательно, интервалы вогнутости и выпуклости равны:
Выпуклый
![]()
:
![]()
Вогнутый
![]()
:
![]()
Однако, хотя и происходит изменение кривизны при x=-1 и x=1, это не точки перегиба. Потому что они не принадлежат к области функционирования.
И, наконец, построим график функции, используя все выполненные вычисления:
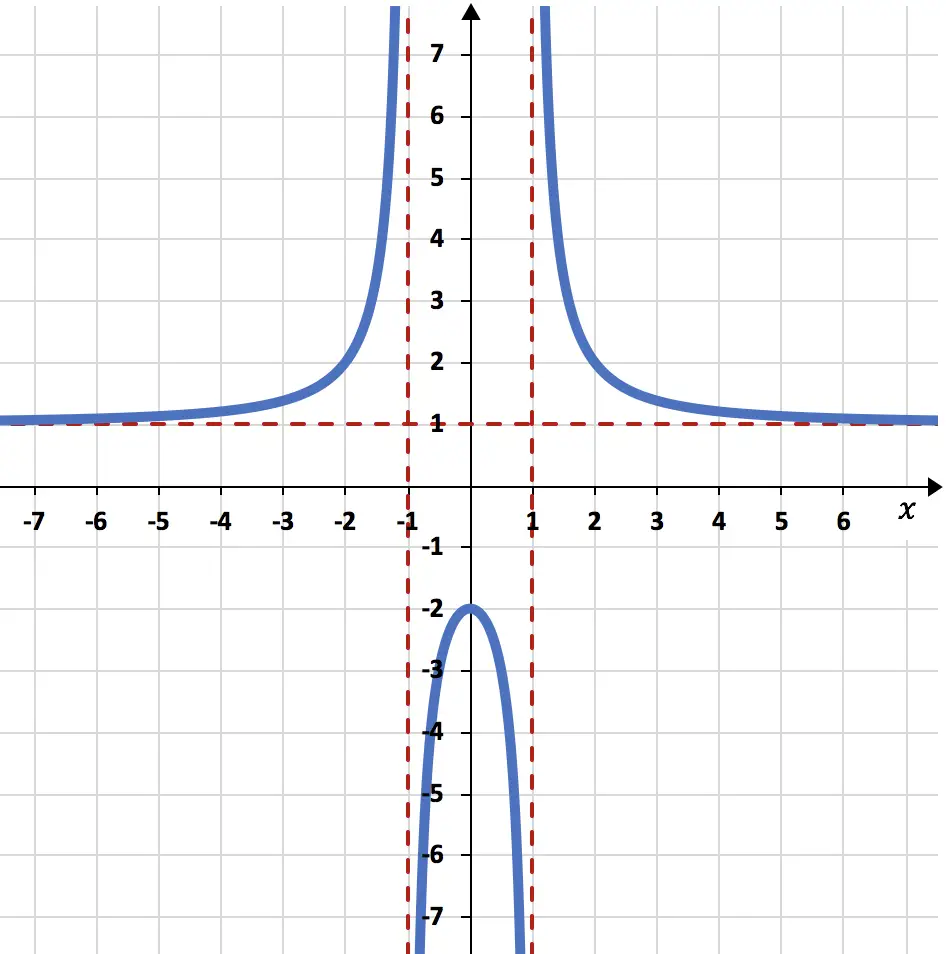
Упражнение 3
Постройте на графике следующую рациональную функцию:
![]()
Это рациональная функция, поэтому нам нужно установить знаменатель равным 0, чтобы увидеть, какие числа не принадлежат области определения функции:
![]()
![]()
![]()
![]()
![]()
Чтобы найти точку пересечения с осью X, решаем
![]()
Поскольку функция всегда имеет значение 0 по оси X:
![]()
![]()
![]()
![]()
![]()
Таким образом, точка пересечения с осью X равна:
![]()
И чтобы найти точку пересечения с осью Y, вычисляем
![]()
Поскольку x всегда равен 0 по оси Y:
![]()
Таким образом, точка пересечения с осью Y равна:
![]()
В этом случае точка пересечения с осью X совпадает с точкой пересечения с осью Y, поскольку функция проходит через начало координат.
Чтобы узнать, имеет ли функция вертикальные асимптоты, нам нужно вычислить предел функции в точках, не принадлежащих области определения (в данном случае x=-2 и x=+2). А если результат бесконечен, то это вертикальная асимптота. Еще:
![]()
Поскольку предел функции при приближении x к -2 дает бесконечность, x=-2 является вертикальной асимптотой.
Вычислим боковые пределы асимптоты x=-2, подставив в функцию очень близкое к ней число:
![]()
![]()
Теперь посмотрим, является ли x=+2 вертикальной асимптотой:
![]()
Поскольку предел функции при приближении x к +2 дает бесконечность, x=+2 является вертикальной асимптотой.
Вычислим боковые пределы асимптоты x=2, подставив в функцию очень близкое к ней число:
![]()
![]()
С другой стороны, горизонтальная асимптота функции будет результатом бесконечного предела функции. Еще:
![]()
Бесконечный предел функции дал нам +∞, поэтому у функции нет горизонтальной асимптоты.
Теперь вычислим наклонную асимптоту. Наклонные асимптоты имеют вид
![]()
И
![]()
Он рассчитывается по следующей формуле:
![]()
![]()
![]()
Зная наклон наклонной асимптоты, мы определяем точку пересечения по следующей формуле:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-de4326a40acf34b64a28c9da8250bf00_l3.png)
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-13478ac6f6fac958ec8b2a714c28bc3d_l3.png)
Но мы получаем неопределенность ∞ – ∞. Поэтому необходимо привести слагаемые к общему знаменателю. Для этого умножим и разделим х на знаменатель дроби:
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e939b43a3405ba644d4b60bb4bacadb_l3.png)
![]()
![]()
Короче говоря, наклонная асимптота:
![]()
![]()
![]()
Чтобы изучить монотонность функции, необходимо сначала вычислить ее производную:
![]()
![]()
Теперь приравняем производную к 0 и решим уравнение:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dc1f64cdcd293da4fee1ef02fff9a588_l3.png)
Теперь мы представляем на прямой все найденные особые точки, то есть точки, которые не принадлежат области определения (x=-2 и x=+2) и те, которые сокращают производную (x=0, x=- 3,46 и х= +3,46):

И мы оцениваем знак производной в каждом интервале, чтобы узнать, увеличивается или уменьшается функция. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет производная в этой точке:
![]()
![]()
![]()
![]()
![]()
![]()
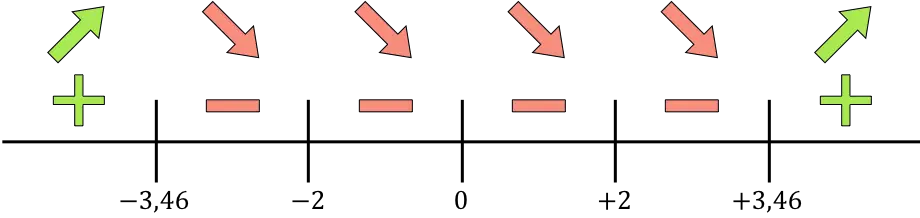
Если производная положительна, это означает, что функция возрастает, а если производная отрицательна, это означает, что функция убывает. Следовательно, интервалы роста и падения составляют:
Рост:
![]()
Снижаться:
![]()
Функция переходит от возрастания к убыванию при x=-3,46, поэтому x=-3,46 является максимумом функции. А функция переходит от убывания к увеличению при x=3,46, поэтому x=3,46 является минимумом функции.
Определяем координаты Y относительных концов:
![]()
![]()
Таким образом, относительные экстремумы функции таковы:
Максимум в точку
![]()
Минимум для точки
![]()
Для изучения кривизны функции вычислим вторую производную функции:



![]()
![]()
![]()
![]()
Теперь приравняем вторую производную к 0 и решим уравнение:
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-31adba554b44aa92fd7227506440ccaf_l3.png)
![]()
Решения нет, поскольку из действительного числа нет отрицательного корня.
Теперь мы представим на прямой все найденные особые точки, то есть точки, которые не принадлежат области определения (x=-2 и x=+2) и те, которые сокращают вторую производную (x=0):

И мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Поэтому мы берем точку в каждом интервале (никогда не особые точки) и смотрим, какой знак имеет вторая производная в этой точке:
![]()
![]()
![]()
![]()

Если вторая производная положительна, это означает, что функция выпуклая.
![]()
, и если вторая производная отрицательна, это означает, что функция вогнутая
![]()
. Следовательно, интервалы вогнутости и выпуклости равны:
Выпуклый
![]()
:
![]()
Вогнутый
![]()
:
![]()
Однако, хотя и происходит изменение кривизны в точках x=-2 и x=+2, это не точки перегиба. Потому что x=-2 и x=+2 не принадлежат области определения функции. С другой стороны, при x=0 происходит изменение кривизны (функция переходит от выпуклой к вогнутой), и это принадлежит функции, поэтому x=0 является точкой перегиба.
Подставим найденные точки перегиба в исходную функцию, чтобы найти другую координату точки перегиба:
![]()
Таким образом, поворотными моментами функции являются:
Поворотные моменты:
![]()
Наконец, на основе всей рассчитанной нами информации, представляем функцию:
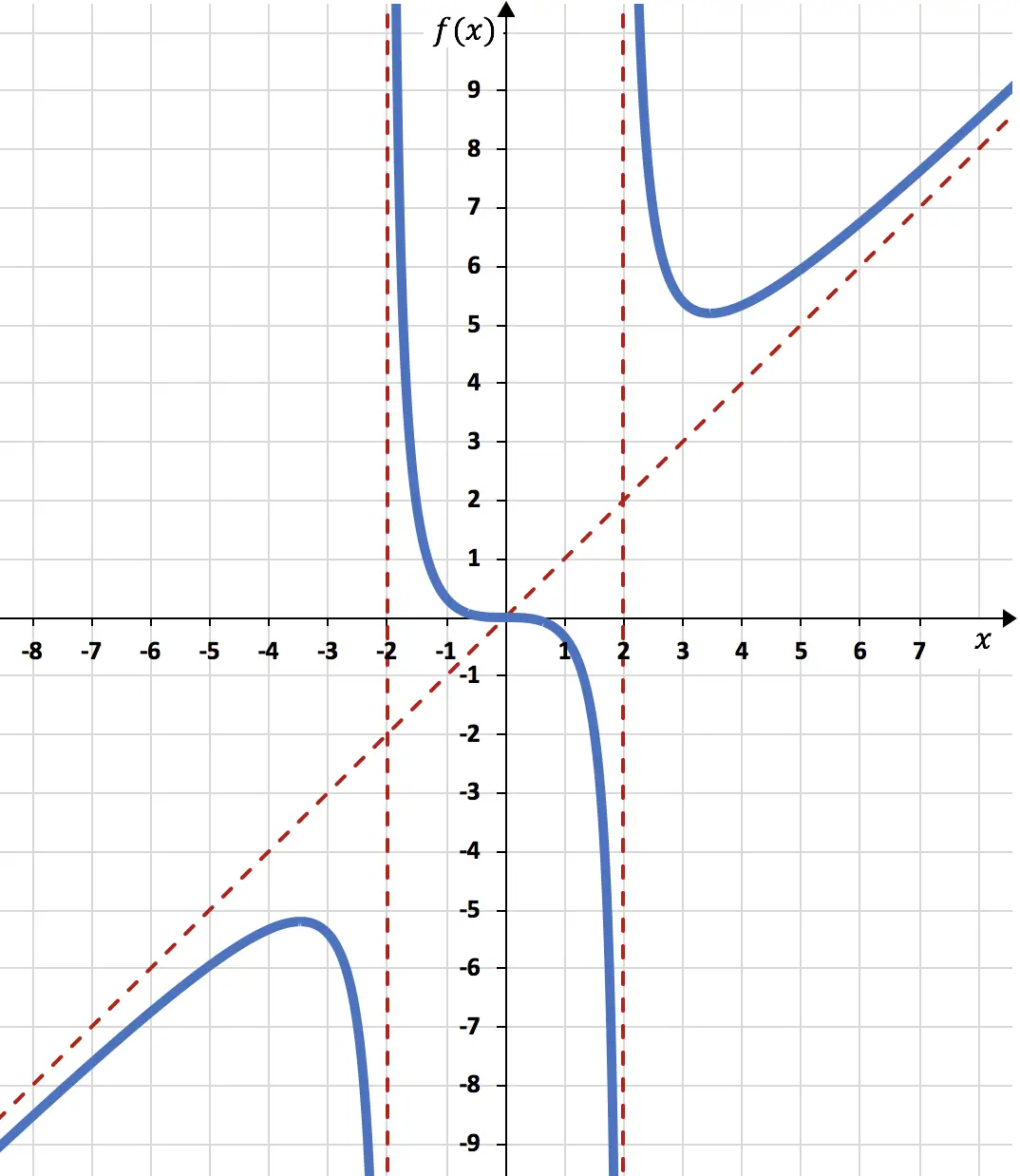
Комментарий: Обратите внимание, что функция пересекает наклонную асимптоту в точке
![]()
Действительно, наклонные асимптоты определяют, прежде всего, поведение функции при стремлении x к +∞ и -∞, фактически функция никогда не пересекает наклонную асимптоту справа от графика (x→+∞) и слева от графика. граф (x→-∞). Однако функция пересекает наклонную асимптоту посередине очень редко, это очень частный случай.