Точки перегиба функции -

Здесь мы объясним, что такое точка перегиба функции и как найти все точки перегиба функции. Дополнительно вы найдете пошаговые упражнения на кривизну и точки перегиба функции.

Каковы точки перегиба функции?

Точками перегиба функции являются точки, в которых график функции меняет кривизну, то есть в точке перегиба функция меняет форму с вогнутой на выпуклую или наоборот.

Как определить, есть ли у функции точка перегиба

Учитывая определение точки перегиба, давайте посмотрим, как узнать, является ли определенная точка точкой перегиба функции.

Функция имеет точку перегиба в точках, которые сокращают ее вторую производную, а ее третья производная не равна нулю.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

В качестве примера вычислим точки перегиба следующей функции третьей степени:

$f(x)=x^3-5x$

Сначала вычисляем вторую и третью производные функции:

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

Теперь приравняем вторую производную к 0 и решим полученное уравнение:

$6x=0$

$x=0$

Тогда точка x=0 будет точкой перегиба функции, если третья производная в этой точке не равна нулю. В нашем случае третья производная всегда равна 6.

$f'''(0)=6\neq 0$

Следовательно, x=0 является точкой перегиба функции.

Как изучить кривизну и найти точки перегиба функции

Мы только что рассмотрели метод нахождения поворотных точек. Однако мы обычно склонны изучать кривизну функции, то есть определять вогнутость и выпуклость функции, а затем вычислять точки перегиба.

Чтобы найти точки перегиба функции через ее кривизну, необходимо выполнить следующие действия:

Найдите точки, не принадлежащие области определения функции.
Вычислите первую производную и вторую производную функции.
Найдите корни второй производной , то есть вычислите точки, которые сокращают вторую производную, решив
$f''(x)=0$

.
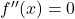
Сделайте интервалы между корнями производной и точками, не принадлежащими области определения функции.
Вычислите значение второй производной в точке каждого интервала.
Знак второй производной определяет вогнутость или выпуклость функции на этом интервале:
- Если вторая производная функции положительна, то функция выпуклая на этом интервале.
- Если вторая производная функции отрицательна, функция на этом интервале вогнутая .
Точки перегиба — это точки, в которых функция меняет форму с выпуклой на вогнутую или наоборот.

Чтобы вы могли увидеть, как вычисляются точки перегиба функции с помощью этой процедуры, мы пошагово решим пример ниже:

Изучите кривизну и найдите точки перегиба следующей полиномиальной функции:

$f(x)=x^4-6x^2$

Первое, что нужно сделать, это вычислить область определения функции. Это полиномиальная функция, поэтому область определения функции состоит из действительных чисел, то есть это непрерывная функция:

$\text{Dom } f= \mathbb{R}$

После того как мы вычислили область определения функции, нам необходимо изучить, в каких точках она выполняется.

$f''(x)=0$

Поэтому сначала вычисляем первую производную функции:

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

Далее вычисляем вторую производную функции:

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

А теперь приравняем вторую производную к 0 и решим уравнение:

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

После того, как мы вычислили область определения функции и

$f''(x)=0$

, представим все найденные критические точки на числовой прямой:

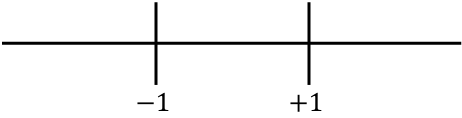
А теперь мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Поэтому мы берем точку в каждом интервале (никогда не критические точки) и смотрим, какой знак имеет вторая производная в этой точке:

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

Если вторая производная положительна, это означает, что функция выпуклая.

$(\bm{\cup})$

, и если вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Следовательно, интервалы вогнутости и выпуклости функции равны:

Выпуклый

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-1,1)}$

Кроме того, при x=-1 функция переходит от выпуклой к вогнутой, поэтому x=-1 является точкой перегиба функции . А при x=1 функция переходит от вогнутой к выпуклой, поэтому x=1 также является точкой перегиба функции.

Наконец, подставляем найденные точки в исходную функцию, чтобы найти координату Y точек перегиба:

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

Таким образом, поворотными моментами функции являются:

Поворотные моменты:

$\bm{(-1,-5)}$

$\bm{(1,-5)}$

Ниже вы можете увидеть графическое представление изучаемой функции:

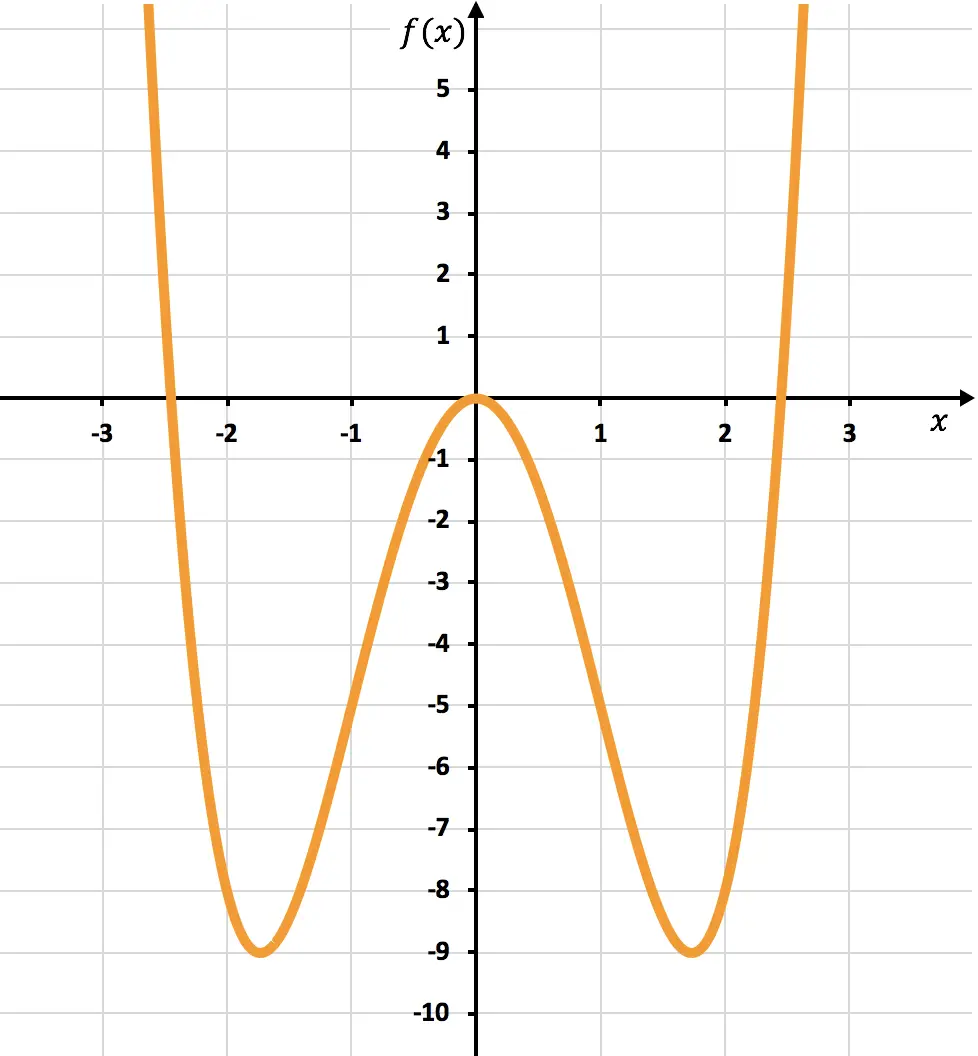
Как видно из графика, функция идет из выпуклой

$(\cup)$

быть вогнутым

$(\cap)$

$(-1,-5)$

так как его кривизна меняется. А с другой стороны, функция идет от вогнутой

$(\cap)$

быть выпуклым

$(\cup)$

$(1,-5)$

Решаемые поворотные упражнения

Упражнение 1

Рассчитайте интервалы вогнутости и выпуклости, а также точки перегиба следующей показательной функции:

$f(x) = xe^x$

Посмотреть решение

Первое, что нужно сделать, это вычислить область определения функции. Функция состоит из полиномиальной функции (x), область определения которой состоит только из действительных чисел, и экспоненциальной функции ( ^ex ), область определения которой также состоит из действительных чисел. Следовательно, область определения функции состоит из действительных чисел:

$\text{Dom } f= \mathbb{R}$

Теперь вычислим производную функции. В данном случае функция состоит из произведения двух функций, поэтому для получения функции нам нужно применить формулу производной произведения:

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

Далее вычисляем вторую производную функции:

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

Положим вторую производную равной 0 и решим уравнение:

$f''(x)= 0$

$2e^x+xe^x= 0$

Выделим общий множитель:

$e^x(2+x)=0$

Чтобы умножение было равно 0, один из двух элементов умножения должен быть нулем. Поэтому мы устанавливаем каждый фактор равным 0:

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

Число, возведенное в другое, никогда не может дать 0. Следовательно, уравнение

$e^x=0$

Решения нет.

Все полученные особые точки представим справа:

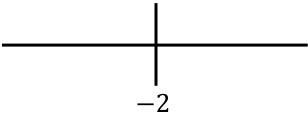
А теперь мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Для этого возьмем точку в каждом интервале и посмотрим, какой знак имеет вторую производную в этой точке:

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

Если вторая производная положительна, это означает, что функция выпуклая.

$(\bm{\cup})$

, и если вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Следовательно, интервалы вогнутости и выпуклости равны:

Выпуклый

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

Кроме того, функция меняется с вогнутой на выпуклую при x=-2, поэтому x=-2 является точкой перегиба функции.

Наконец, мы подставляем найденную точку перегиба в исходную функцию, чтобы найти координату Y точки:

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

В заключение, единственными поворотными моментами функции являются:

Поворотные моменты:

$\bm{(-2,-2e^{-2})}$

Упражнение 2

Изучите интервалы вогнутости и выпуклости и найдите точки перегиба следующей рациональной функции:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Посмотреть решение

Сначала нам нужно вычислить область определения функции. Поскольку это рациональная функция, мы приравниваем знаменатель к нулю, чтобы увидеть, какие числа не принадлежат области определения функции:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Это означает, что когда x равен -2 или +2, знаменатель будет равен 0. И, следовательно, функция не будет существовать. Таким образом, область определения функции состоит из всех чисел, кроме x=-2 и x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Во-вторых, вычисляем первую производную функции:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

И затем решаем вторую производную:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Все члены умножаются на

$(x^2-4)$

. Таким образом, мы можем упростить дробь:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Теперь вычислим корни второй производной функции:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Термин

$\left(x^2-4\right)^3$

Это предполагает деление всей левой части, чтобы мы могли умножить ее на всю правую часть:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Выделим общий множитель:

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Решения нет, поскольку из действительного числа нет отрицательного корня.

Теперь мы представим на прямой все полученные критические точки, то есть точки, которые не принадлежат области определения (x=-2 и x=+2) и те, которые сокращают вторую производную (x=0):

И мы оцениваем знак второй производной в каждом интервале, чтобы узнать, является ли функция вогнутой или выпуклой. Итак, мы берем точку в каждом интервале и смотрим, какой знак имеет вторая производная в этой точке:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Если вторая производная положительна, это означает, что функция выпуклая.

$(\bm{\cup})$

, и если вторая производная отрицательна, это означает, что функция вогнутая

$(\bm{\cap})$

. Следовательно, интервалы вогнутости и выпуклости равны:

Выпуклый

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Вогнутый

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Функция меняет кривизну в трех точках, поэтому рациональная функция в принципе будет иметь три точки перегиба: x=-2, x=0 и x=2. Однако, хотя и происходит изменение кривизны при x=-2 и x=+2, это не точки перегиба, поскольку они не принадлежат области определения функции. С другой стороны, при x=0 происходит изменение кривизны, и это принадлежит функции, поэтому x=0 является единственной точкой перегиба функции.

Остаётся только вычислить координату Y точки перегиба:

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

Короче говоря, единственной точкой перегиба рациональной функции является начало координат:

Поворотные моменты:

$\bm{(0,0)}$

Упражнение 3

Мы знаем, что функция

$f(x)=x^3+ax^2+bx+c$

пройти через точку

$(3,1)$

, имеет относительный экстремум в

$x=1$

и поворотный момент в

$x = 2$

. На основе этой информации рассчитайте значения параметров.

$a, b$

$c$

Посмотреть решение

Пусть функция имеет точку перегиба в точке

$x= 2$

Значит это

$f''(2)=0$

. Поэтому вычисляем вторую производную функции в

$x= 2$

и мы устанавливаем его равным 0:

$f(x) = x^3+ax^2+bx+c \ \longrightarrow \ f'(x)=3x^2+2ax+b$

$f'(x)=3x^2+2ax+b \ \longrightarrow \ f''(x)= 6x+2a$

$\left. \begin{array}{l} f''(2)=6\cdot 2+2a\\[2ex] f''(2)=0\end{array} \right\} \longrightarrow 6\cdot 2+2a=0$

И решаем полученное уравнение, чтобы найти значение параметра а:

$6\cdot 2+2a=0$

$12+2a=0$

$2a=-12$

$a=\cfrac{-12}{2}$

$\bm{a=-6}$

Таким образом, функция будет:

$f(x)=x^3+ax^2+bx+c \ \xrightarrow{a \ = \ -6}\ f(x)=x^3-6x^2+bx+c$

Кроме того, функция имеет экстремум

$x= 1$

, Которое значит что

$f'(1)=0$

. Поэтому вычисляем первую производную функции в

$x= 1$

и мы устанавливаем его равным 0:

$f(x)=x^3-6x^2+bx+c \ \longrightarrow \ f'(x)=3x^2-12x+b$

$\left. \begin{array}{l} f'(1)=3\cdot 1^2-12\cdot 1+b\\[2ex] f'(1)=0\end{array} \right\} \longrightarrow 3\cdot 1^2-12\cdot 1+b=0$

И решаем полученное уравнение, чтобы найти значение неизвестного b:

$3\cdot 1^2-12\cdot 1+b=0$

$3 \cdot 1 -12 + b = 0$

$3 -12 + b = 0$

$b=+12-3$

$\bm{b=9}$

Таким образом, функция будет:

$f(x)=x^3-6x^2+bx+c \ \xrightarrow{b \ = \ 9} \ f(x)=x^3-6x^2+9x+c$

С другой стороны, они говорят нам, что функция проходит через точку (3,1). Это сказать,

$f(3)=1$

. Следовательно, мы можем применить это условие, чтобы найти значение параметра c:

$\left. \begin{array}{l} f(3)=3^3-6\cdot 3^2+9\cdot3+c \\[2ex] f(3)=1 \end{array} \right\} \longrightarrow 3^3-6\cdot 3^2+9\cdot 3+c = 1$

И решаем полученное уравнение, чтобы найти значение

$b:$

$3^3-6\cdot 3^2+9\cdot 3+c = 1$

$27-6\cdot 9+27+c = 1$

$27-54+27+c = 1$

$c=1-27+54-27$

$\bm{c=1}$

Таким образом, функция будет:

$f(x)=x^3-6x^2+9x+c \ \xrightarrow{c \ = \ 1} \ f(x)=x^3-6x^2+9x+1$

Каковы точки перегиба функции?

Как определить, есть ли у функции точка перегиба

Как изучить кривизну и найти точки перегиба функции

Решаемые поворотные упражнения

Упражнение 1

Упражнение 2

Упражнение 3

Оставьте комментарий Отменить ответ