Здесь вы узнаете, как получить секанс функции. Кроме того, вы сможете увидеть несколько упражнений, решаемых поэтапно на производную секущей. И, наконец, вас ждет демонстрация формулы этого типа тригонометрической производной.
Что является производной секанса?
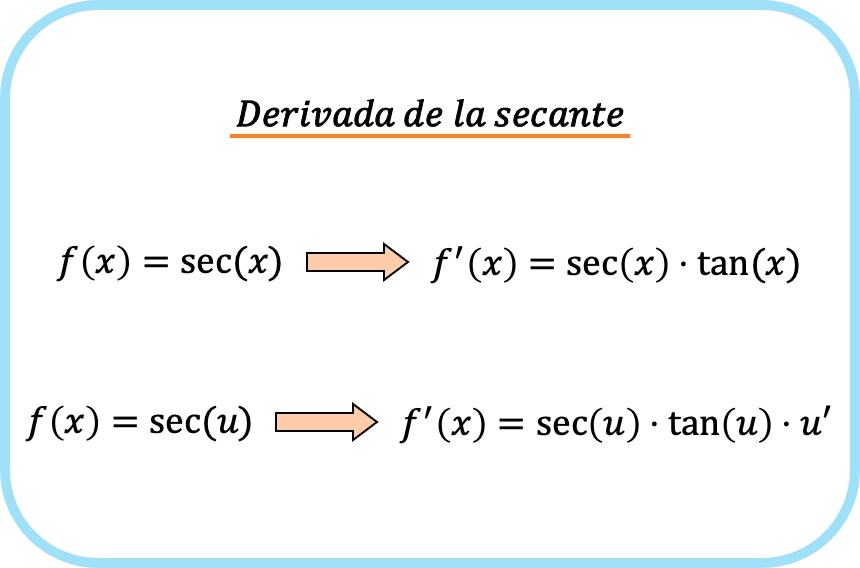
Производная секущего x равна произведению секущего x и тангенса x.
![]()
Применяя тригонометрические формулы, производную секущего x можно также определить как частное синуса x, деленного на квадрат косинуса x.
![]()
И если мы применим правило цепочки, производная секущей функции будет произведением секущего функции, умноженного на тангенс функции, умноженного на производную функции.
![]()
Вкратце, формула производной секанса выглядит следующим образом:
Примеры производной секанса
После того, как мы увидели, какова формула производной секущей, мы решим несколько примеров этого типа тригонометрических производных.
Пример 1: Производная секущего 2x
В этом примере мы увидим, сколько стоит производная секущего 2x:
![]()
Чтобы получить секанс функции 2x, необходимо использовать соответствующую формулу. Кроме того, в аргументе секущей у нас есть функция, отличная от x, поэтому нам нужно применить правило цепочки.
![]()
Функция 2x линейна, поэтому ее производная равна 2. Поэтому, чтобы найти производную, мы просто заменяем u на 2x, а u’ на 2 в формуле:
![]()
Пример 2: Производная секущего x в квадрате
В этом упражнении мы увидим, какова производная секущего х в квадрате:
![]()
Чтобы получить секанс функции, вы можете использовать одну из двух формул, представленных выше, но в этом случае мы будем дифференцировать функцию с помощью формулы умножения секущего на тангенс.
![]()
Производная x, возведенная в степень 2, дает 2x, поэтому производная секущего x в квадрате равна:
![]()
Пример 3: Производная секущего куба многочлена
![]()
Правило для производной секущей функции:
![]()
Но в данном случае мы должны вывести составную функцию, так как секанс возводится в третью степень и при этом в его аргументе мы имеем полиномиальную функцию. Итак, чтобы дифференцировать всю функцию, нам нужно применить правило цепочки:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
Решенные упражнения на производную секущей
Выведите следующие секущие функции:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
Демонстрация формулы производной секущей
Далее докажем формулу производной секущей. Хотя очевидно, что не обязательно знать доказательство наизусть, всегда полезно понять, откуда берутся формулы.
Математически секанс представляет собой мультипликативную величину, обратную косинусу:
![]()
Поэтому мы можем попытаться вывести секанс, используя правило частного:
![]()
И, как мы видели в первом разделе, предыдущее выражение можно преобразовать в формулу производной секанса. Для этого разделим дробь на две разные фракции:
![]()
Деление синуса на косинус эквивалентно тангенсу, поэтому заменим указанное частное на тангенс:
![]()
Согласно математическому определению секущей функции, косинус является ее обратным мультипликативом. Таким образом, заменив единицу, разделенную косинусом, на секущую, мы придем к формуле ее производной:
![]()