Здесь вы узнаете, что такое цепное правило и как выводить функции с помощью цепного правила. Кроме того, вы сможете увидеть несколько примеров производных, решенных с помощью цепного правила, и даже сможете попрактиковаться в пошаговых упражнениях по решению производных с применением цепного правила.
Что такое правило цепочки?
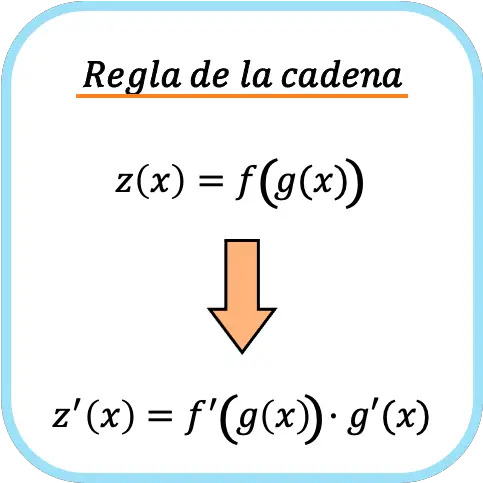
Цепное правило — это формула, используемая для вывода сложных функций. Цепное правило гласит, что производная сложной функции f(g(x)) равна производной f'(g(x)) умноженной на производную g'(x) .
➤ См.: составная функция
Неформально часто говорят, что правило цепочки состоит в том, чтобы дифференцировать функцию и затем умножить ее на то, что в ней находится .
Формула цепного правила позволяет нам гораздо легче дифференцировать составные функции, потому что, если бы мы должны были дифференцировать композицию функций, используя предел определения производной, нам пришлось бы выполнить много вычислений.
С другой стороны, необходимо учитывать, что это правило применяется только для нахождения производной сложных функций, а не каких-либо функций или операций с функциями. Например, очень распространенной ошибкой является неправильное применение правила цепочки в таких функциональных продуктах, как следующее:
![]()
❌
Правило цепочки можно использовать только тогда, когда у нас есть одна функция внутри другой .
![]()
✅
Примеры производных инструментов с цепным правилом
Учитывая определение цепного правила, мы выведем несколько функций на примере цепного правила. Помните, что если в примере вы не понимаете, как выводится функция с помощью правила цепочки, вы можете задать нам вопрос в комментариях!
Пример 1
В этом примере мы будем использовать цепное правило для получения натурального логарифма x в квадрате:
![]()
Производная натурального логарифма равна 1 разу его аргумента, поэтому производная
![]()
быть:
![]()
![]()
С другой стороны, производная x, возведенная в степень двойки, равна 2x:
![]()
Наконец, мы вычисляем производную всей функции, применяя цепное правило. Производная сложной функции будет произведением двух только что найденных нами производных:
![]()
![]()
Пример 2
Во втором примере мы выведем потенциальную функцию на основе полинома:
![]()
Чтобы получить степень, нам нужно поместить перед ней исходный показатель степени и вычесть из показателя одну единицу, чтобы производная потенциальной функции без применения правила цепочки была бы:
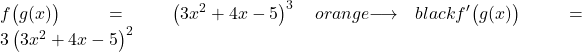
Теперь выводим то, что в скобках:
![]()
И, наконец, мы используем цепное правило для решения производной всей функции, которая будет произведением двух рассчитанных ранее производных:
![]()
![]()
Пример 3
В этом случае мы найдем производную синуса x в кубе плюс 7x:
![]()
Действительно, это композиция функций, поскольку у нас есть функция x 3 +7x внутри функции синуса, поэтому мы можем использовать цепное правило, чтобы найти производную сложной функции.
С одной стороны, производная синуса – это косинус, поэтому производной внешней функции будет косинус с тем же аргументом, что и синус:
![]()
А с другой стороны, производная х 3 +7х равна 3х 2 +7.
![]()
Следовательно, производная сложной функции является произведением двух производных:
![]()
![]()
Решенные упражнения на производные с помощью цепного правила
Упражнение 1
Выведите следующую составную функцию, используя цепное правило:
![]()
Внешняя функция является потенциальной функцией, поэтому для вычисления ее производной необходимо применить следующую формулу:
![]()
![]()
А затем вычисляем производную функции внутри. Это вычитание степеней, поэтому для вычисления его производной необходимо применить к каждому из ее членов следующую формулу:
![]()
![]()
![]()
Короче говоря, производная сложной функции — это произведение двух найденных производных:
![]()
![]()
Упражнение 2
Решите производную следующей сложной функции, используя цепное правило:
![]()
Сначала находим производную внешней функции:
![Rendered by QuickLaTeX.com \begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e5d21c7196c7ebaeaf6ca11762ca251_l3.png)
А теперь решаем производную внутренней функции:
![]()
Таким образом, производная всей функции равна:
![]()
![]()
Упражнение 3
С помощью цепного правила вычислите производную следующей композиции функций:
![]()
Это показательная функция, поэтому для расчета ее производной необходимо применить следующую формулу:
![]()
![]()
Также дифференцируем функцию от показателя функции:
![]()
И мы используем цепное правило, чтобы найти производную целочисленной составной функции:
![]()
![]()
Упражнение 4
Найдите производную следующей сложной функции, используя цепное правило:
![]()
Это композиция функций, потому что в аргументе иррациональной функции мы имеем синусоидальную функцию и линейную функцию. Итак, сначала вычислим производную от корня:
![]()
![Rendered by QuickLaTeX.com f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e909efbe50930f94cce0b2485b060046_l3.png)
И теперь мы получаем аргумент от радикала. Это сумма функций, поэтому производная будет суммой производных каждого члена:
![]()
Таким образом, производная всей функции равна произведению двух вычисленных производных:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fad132b49a5faab86a3955efd5422973_l3.png)
Упражнение 5
Используя правило цепочки, выведите следующую композицию функций:
![]()
Чтобы применить цепное правило, вы должны найти производную степени и многочлена, а затем умножить их. Таким образом, выводим мощность по соответствующей формуле:
![]()
![]()
Во-вторых, мы выводим полиномиальную функцию из показателя степени:
![]()
А цепное правило говорит нам, что производная всей функции — это произведение только что найденных нами производных:
![]()
![]()
Упражнение 6
![]()
Очевидно, что функция в этой задаче составная, так как в аргументе натурального логарифма мы имеем произведение двух разных видов функций. Итак, сначала дифференцируем логарифм:
![]()
![]()
Во-вторых, мы получаем функцию из аргумента логарифма. Это умножение двух функций, поэтому для вывода необходимо использовать следующую формулу:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-643ddf7ec82cbcc3bc685ceadf59da98_l3.png)
Таким образом, производная целой функции, согласно правилу цепочки, будет произведением двух производных:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6912d0951fb85a61df21cbed282000f2_l3.png)
Упражнение 7
Решите производную следующей функции, используя цепное правило:
![]()
Это композиция функций, поэтому мы будем дифференцировать логарифм и его аргумент отдельно, а затем перемножать производные.
Итак, сначала дифференцируем логарифм по основанию 9:
![]()
![]()
А теперь вычислим производную аргумента логарифма. Обратите внимание, что число e имеет в своем аргументе функцию, т. е. это составная функция, поэтому нам также необходимо применить цепное правило для получения этой функции:
![]()
![]()
Таким образом, производная целого аргумента логарифма будет равна:
![]()
И, наконец, производная всей функции будет произведением f'(g(x)) и g'(x):
![]()
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a702df902c9f1eff66e14836a262c0a_l3.png)
Упражнение 8
Выведите следующую составную функцию, используя цепное правило:
![]()
В этом упражнении у нас есть композиция из нескольких функций, поэтому нам придется применить правило цепочки несколько раз. Сначала выведем тригонометрическую функцию из синуса, производная которого равна косинусу:
![]()
А теперь вычисляем производную аргумента синуса, используя цепное правило:
![]()
![Rendered by QuickLaTeX.com \begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e1c2492990456e277e493c898cb3924_l3.png)
Наконец, снова применив цепное правило, мы получим производную всего состава функций:
![]()
![]()
Доказательство цепного правила
Наконец, мы докажем формулу цепного правила. Для этого начнем с математического определения производной:
![]()
Пусть z — функция, состоящая из двух функций:
![]()
Тогда производная функции z с применением определения будет:
![]()
Как вы уже знаете, дробь можно умножать и делить на одно и то же слагаемое, ведь результат от этого не меняется. Поэтому мы можем перейти к следующему шагу:
![]()
Переставим знаменатели дробей:
![]()
Применяя свойства пределов, мы можем разделить вышеуказанный предел на два. Поскольку предел произведения равен произведению пределов:
![]()
И это выражение эквивалентно следующему:
![]()
Таким образом, формула цепного правила доказана, поскольку мы пришли к ней из определения производной.