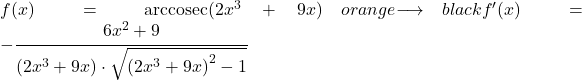На этой странице вы увидите, какова формула производной арккосеканса. Кроме того, вы сможете увидеть решенные упражнения на производные дугового косеканса функции.
Формула производной арккосеканса
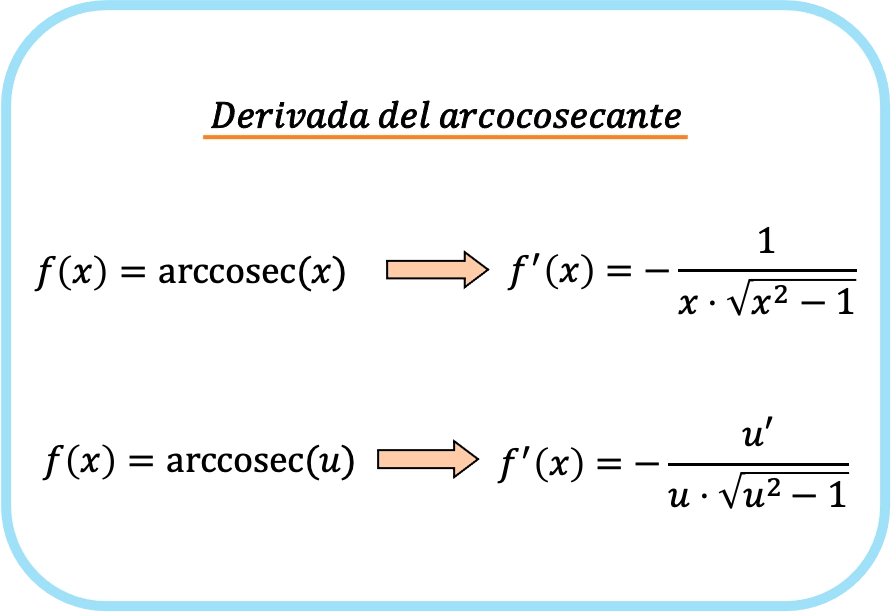
Производная арккосеканса x является отрицательной единицей по произведению x на корень из x в квадрате минус 1.
![]()
Следовательно, производная арккосеканса функции равна минус частному производной этой функции, деленному на функцию, умноженную на корень этой функции, возведенный в квадрат минус один.
![]()
По сути, предыдущие две формулы одинаковы, но во втором выражении применяется правило цепочки. Фактически, если вы подставите тождественную функцию x в u, вы получите производную арккосеканса x, поскольку производная x равна единице.
Как известно, арккосеканс — это обратная тригонометрическая функция косеканса, однако ее производные совсем другие. Вы можете увидеть формулу для этого другого типа тригонометрической функции по следующей ссылке:
➤ См.: производная косеканса
Примеры производной косекансной дуги
Увидев, что такое правило производной арккосеканса, мы затем решим два примера производной этого типа. Но если у вас остались вопросы о том, как вывести косекансную дугу, вы можете задать их нам в комментариях.
Пример 1
На этом примере мы увидим, чему равна производная косеканса дуги квадратичной функции x 2 .
![]()
Чтобы вычислить производную арккосеканса x в квадрате, мы применим формулу, которую мы видели выше:
![]()
Производная x в степени двойки равна 2x, поэтому производная составной функции равна:
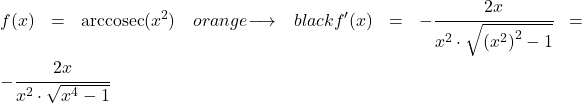
Пример 2
Во втором примере мы выведем арккосеканс потенциальной функции.
![]()
Нам нужно использовать правило производной арксеканса, чтобы найти производную всей функции.
![]()
Итак, в числителе пишем производную аргумента функции, а в знаменателе переписываем потенциальную функцию и умножаем ее на корень квадратный из функции аргумента, возведенного в квадрат минус 1: