Производная косеканса

В этой статье мы объясним, как получить косеканс функции (формулы). Вы также найдете упражнения, решаемые шаг за шагом для производной косеканса. И, наконец, вы сможете увидеть демонстрацию формулы этого типа тригонометрической производной.

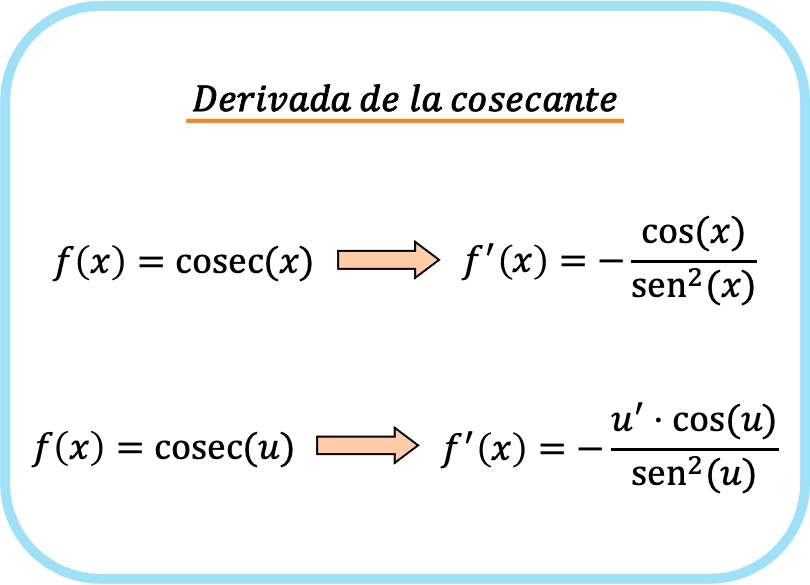
Формула производной косеканса

Производная косеканса x равна минус частному косинуса x, деленного на квадрат синуса x.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

Используя тригонометрические формулы, мы также можем определить производную косеканса x как минус произведение котангенса x на косеканс x.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

И если мы применим цепное правило, производная косеканса функции будет равна произведению производной функции, умноженному на косинус функции, разделенному на квадрат синуса функции.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Таким образом, формула, используемая для получения косеканса функции, выглядит следующим образом:

Примеры производной косеканса

Увидев, какова формула производной косеканса, приведем теперь несколько примеров. Таким образом, вы можете точно увидеть, как получается косеканс функции.

Пример 1: Производная косеканса 2x

В этом примере мы увидим, сколько составляет производная косеканса 2x:

$f(x)=\text{cosec}(2x)$

Функция аргумента косеканса отличается от x, поэтому нам нужно использовать правило косекансной производной с правилом цепочки.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Итак, чтобы найти производную этой тригонометрической функции, достаточно просто подставить значения в предыдущую формулу: в аргументе косинус и синус мы ставим 2x, а u’ соответствует производной 2x, т.е. 2:

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

Пример 2: Производная косеканса x в квадрате

В этом упражнении мы увидим, чему равна производная косеканса x в квадрате:

$f(x)=\text{cosec}(x^2)$

Логически производная этой тригонометрической функции решается по формуле производной косеканса:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Производная x в квадрате дает 2x, поэтому производная косеканса x в степени двойки равна:

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

Пример 3: Производная кубического косеканса показательной функции

$f(x)=\text{cosec}^3(e^{5x})$

Каким бы ни был аргумент функции, правило для производной косеканса функции следующее:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

Но в данном случае мы имеем составную функцию, потому что косеканс повышен до трёх и к тому же в её аргументе присутствует показательная функция. Итак, чтобы дифференцировать всю функцию, нам нужно несколько раз применить правило цепочки:

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

Решенные задачи о производной косеканса

Выведите следующие косекансные функции:

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

посмотреть решение

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

Доказательство формулы производной косеканса

Далее мы продемонстрируем формулу производной косеканса. В отличие от других демонстраций, в этом случае мы не будем использовать предел, определяющий производную, а начнем с математического определения косеканса.

Алгебраически косекансная тригонометрическая функция является мультипликативной обратной синусоиду:

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

Поэтому мы можем взять производную косеканса, используя правило фактора:

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

Как видите, только применив правило производной от деления, мы приходим к формуле производной косеканса. А поскольку производная частного уже доказана (вы можете увидеть ее по следующей ссылке), то правило косекансной производной также доказано.

➤ См.: доказательство производной частного

Формула производной косеканса

Примеры производной косеканса

Пример 1: Производная косеканса 2x

Пример 2: Производная косеканса x в квадрате

Пример 3: Производная кубического косеканса показательной функции

Решенные задачи о производной косеканса

Доказательство формулы производной косеканса

Оставьте комментарий Отменить ответ