Производная гиперболического синуса

Здесь вы найдете, как вывести гиперболический синус (формула). Кроме того, вы увидите несколько решенных примеров гиперболической производной синуса. И, наконец, докажем формулу производной этого вида тригонометрической функции.

Формула, полученная из гиперболического синуса

Производная гиперболического синуса x является гиперболическим косинусом x.

f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)

Следовательно, производная гиперболического синуса функции равна произведению гиперболического косинуса функции и производной этой функции.

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

По сути, две приведенные выше формулы одинаковы, с той лишь разницей, что во второй формуле мы применяем правило цепочки. А поскольку производная x равна 1, это не меняет функцию.

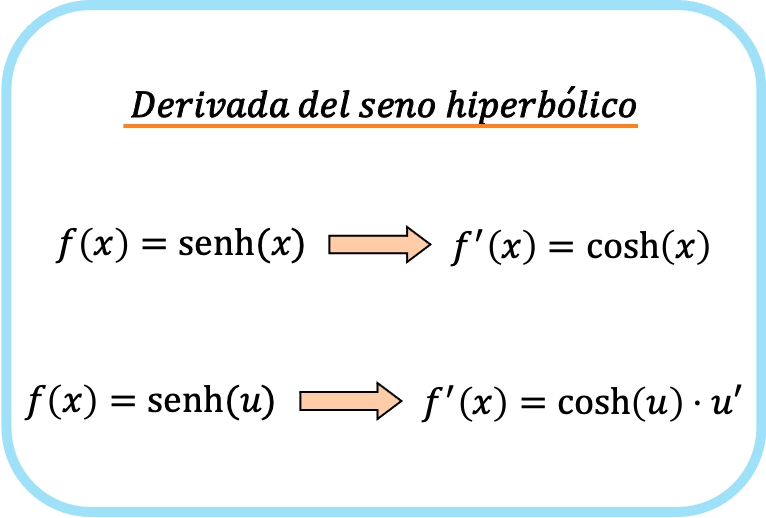
производная гиперболического синуса

Как видите, формула гиперболической производной синуса очень похожа на формулу производной синуса .

Примеры производной гиперболического синуса

Как только мы уже увидели, что представляет собой формула производной гиперболического синуса, мы теперь приступим к решению нескольких примеров производной гиперболического синуса. Итак, наверняка у вас нет сомнений в том, как это делается.

Пример 1: Производная гиперболического синуса 2x

f(x)=\text{senh}(2x)

В этом случае в аргументе гиперболического синуса у нас есть функция, отличная от x, поэтому мы должны использовать формулу производной гиперболического синуса с цепным правилом, чтобы найти производную:

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

Производная 2x равна 2, поэтому производная гиперболического синуса 2x будет гиперболическим косинусом 2x, умноженным на 2.

f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)

Пример 2: Производная гиперболического синуса x в квадрате

f(x)=\text{senh}(x^2)

Формула производной гиперболического синуса:

f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'

С другой стороны, производная квадратичной функции x2 равна 2x. Таким образом, производная всей функции равна:

f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x

Доказательство формулы производной гиперболического синуса

Наконец, мы продемонстрируем формулу для гиперболической производной синуса. Для этого начнем с математического определения гиперболического синуса:

\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}

Теперь выведем две стороны равенства:

\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'

Для вывода правой части уравнения воспользуемся формулой производной от деления:

\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}

➤ См.: производная показательной функции с основанием e

И именно мы пришли к выражению, определяющему гиперболический косинус. Итак, производная гиперболического синуса доказана:

\displaystyle\text{senh}'(x)=\text{cosh}(x)

Оставьте комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

Прокрутить вверх