Здесь мы объясним, как получить арккосинус функции. Кроме того, вы найдете примеры производных арккосинуса и сможете попрактиковаться, выполняя упражнения, решаемые шаг за шагом. Наконец, мы покажем вам доказательство формулы производной арккосинуса.
Что является производной арккосинуса?
Производная арккосинуса x равна отрицательной единице по отношению к квадратному корню из единицы минус x в квадрате.
![]()
Следовательно, производная арккосинуса функции равна минус частному производной этой функции, деленному на квадратный корень из единицы минус квадрат этой функции.
![]()
Фактически, первая формула получается путем замены x на u во второй формуле. Итак, подведем итог: формула производной обратного косинуса:

Как видите, формула производной арккосинуса аналогична формуле производной арксинуса , но с добавлением перед ней минуса.
Примеры производной арккосинуса
Учитывая формулу производной функции арккосинус, мы сейчас разберем несколько примеров такого типа тригонометрических производных. Так вам будет легче понять, как получается арккосинус функции.
Пример 1: Производная арккосинуса 2x
![]()
Для решения производной арккосинуса воспользуемся его формулой:
![]()
Производная 2x равна 2, поэтому арккосинусная производная 2x равна минус 2 относительно корневой единицы минус 2x в квадрате:
![]()
Пример 2: Производная арккосинуса x в квадрате
![]()
Мы применяем формулу производной арккосинуса с правилом цепочки для расчета производной:
![]()
Поскольку производная функции x 2 равна 2x, производная арккосинуса x в степени 2 равна:
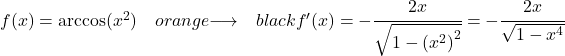
Пример 3: Производная арккосинуса логарифма
![]()
Функция в этом примере представляет собой функцию, состоящую из арккосинуса и натурального логарифма, поэтому для ее получения нам нужно использовать цепное правило.
![]()
Производная натурального логарифма равна единице, разделенной на x, поэтому производная целочисленной функции равна:
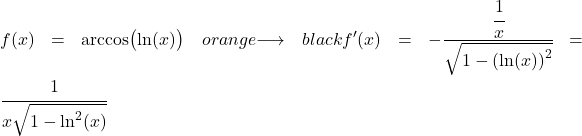
Производная арккосинуса решила проблемы
Выведите следующие функции арккосинуса:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0ffd255c55afc3967dc250bc63741575_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ec25311613f0552bbc52d2d15581d3fb_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d1a362c38a56084dec3c6ebbccba9ab0_l3.png)
Доказательство формулы производной арккосинуса
В этом разделе мы продемонстрируем формулу производной арккосинуса.
![]()
Сначала преобразуем арккосинус в косинус:
![]()
Теперь выведем две стороны равенства:
![]()
Мы очищаем вас:
![]()
Мы используем фундаментальное тригонометрическое тождество, чтобы заменить синус на косинус:
![]()
![]()
Но выше мы пришли к выводу, что x равен косинусу y, поэтому уравнение остается:
![]()
И вот мы пришли к выражению для производной арккосинуса, вот и продемонстрирована его формула.