Производная арксинуса

В этой статье мы объясним, как получить арксинус функции. Вы найдете примеры производных арксинуса функций и даже сможете попрактиковаться, выполняя упражнения, решаемые шаг за шагом. Наконец, вы также увидите демонстрацию формулы производной арксинуса.

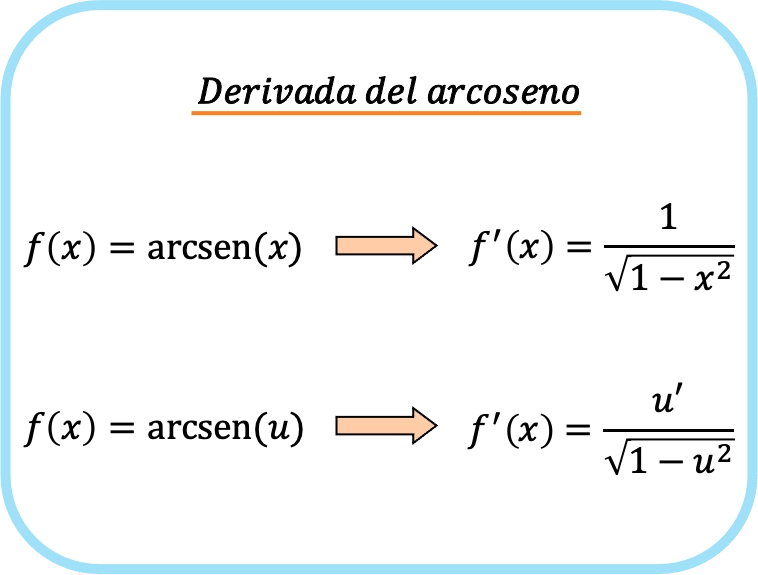
Что является производной арксинуса?

Арксинусная производная x равна единице квадратного корня из единицы минус x в квадрате.

$f(x)=\text{arcsen}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{1-x^2}}$

Следовательно, производная арксинуса функции равна частному производной этой функции, деленному на квадратный корень из единицы минус квадрат функции.

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Логично, что вторая формула получается применением правила цепочки к первой формуле.

Помните, что арксинус — это обратная функция синуса, поэтому его еще называют обратным синусом.

Примеры производной арксинуса

Увидев, какова формула производной арксинуса, мы объясним несколько примеров тригонометрических производных этого типа. Так вам будет легче понять, как получается арксинус функции.

Пример 1: Производная арксинуса 2x

$f(x)=\text{arcsen}(2x)$

Чтобы найти производную функции арксинус, нам нужно воспользоваться соответствующей ей формулой:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Таким образом, производная 2x равна 2, поэтому арксинусная производная 2x равна 2, разделенному на корень из одного минус 2x в квадрате:

$f(x)=\text{arcsen}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\sqrt{1-(2x)^2}}=\cfrac{2}{\sqrt{1-4x^2}}$

Пример 2: Производная арксинуса x в квадрате

$f(x)=\text{arcsen}(x^2)$

Для ее получения воспользуемся формулой производной арксинуса:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Функция x ² имеет вторую степень, поэтому ее производная равна 2x. Таким образом, производная арксинуса x, возведенная в степень 2, равна:

$f(x)=\text{arcsen}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=\cfrac{2x}{\sqrt{1-x^4}}$

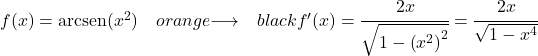
Пример 3: Производная арксинуса e ^x

$f(x)=\text{arcsen}(e^x)$

Функция в этом примере является составной функцией, поэтому нам нужно применить цепное правило для решения производной:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

Производная e ^x равна самой себе, поэтому производная всей функции равна:

$f(x)=\text{arcsen}(e^x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{e^x}{\sqrt{1-\left(e^x\right)^2}}=\cfrac{e^x}{\sqrt{1-e^{2x}}}$

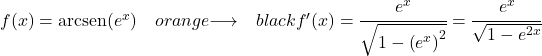
Решенные задачи по производной арксинуса

Выведите следующие арксинусные функции:

$\text{A) }f(x)=\text{arcsen}(6x)$

$\text{B) }f(x)=\text{arcsen}(x^2-4x)$

$\text{C) }f(x)=\text{arcsen}\left(3x^4-6x^3+9+e^{x^2}\right)$

$\text{D) }f(x)=\text{arcsen}\left(\log_5(3x)\right)$

$\text{E) }f(x)=\text{arcsen}\left(\sqrt{4x}\right)$

посмотреть решение

$\text{A) }f'(x)=\cfrac{6}{\sqrt{1-(6x)^2}}=\cfrac{6}{\sqrt{1-36x^2}}$

$\text{B) }f'(x)=\cfrac{2x-4}{\sqrt{1-(x^2-4x)^2}}$

$\text{C) }f'(x)=\cfrac{12x^3-18x^2+2x\cdot e^{x^2}}{\sqrt{1-(3x^4-6x^3+9+e^{x^2})^2}}$

$\text{D) }f'(x)=\cfrac{1}{\sqrt{1-\left(\log_5(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 5}=\cfrac{1}{x\cdot \ln 5\cdot \sqrt{1-\left(\log_5(3x)\right)^2}}$

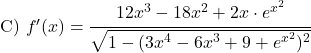
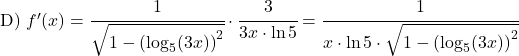
$\begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$