Боковые пределы

В этой статье мы объясним, что такое боковой предел функции (с примерами). Мы также научим вас рассчитывать левый и правый боковой предел функции как графически, так и численно. Кроме того, вы сможете тренироваться с упражнениями, пошагово решающими боковые ограничения.

Каковы боковые пределы?

Боковые пределы функции в точке изучают поведение функции вокруг этой точки. Существует левый боковой предел и правый боковой предел, который анализирует значение функции слева и справа от рассматриваемой точки соответственно.

Боковые пределы слева и справа

Как мы видели в определении боковых границ, существует два типа: левые боковые границы и правые боковые границы.

Левый предел функции обозначается знаком минус в точке анализа предела, а правый предел обозначается знаком плюс.

Посмотрите на следующий пример, чтобы лучше понять значение боковых ограничений:

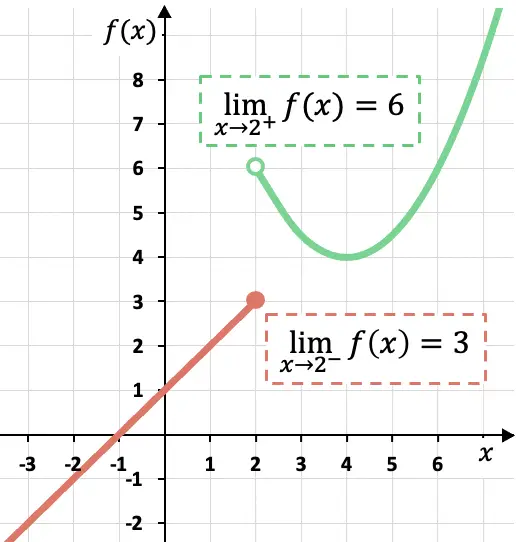
Как видно из графического представления этой кусочной функции, боковые пределы зависят от стороны, на которой они рассчитываются.

В этом случае функция приближается к 3, когда x приближается к 2 слева, поскольку функция принимает значения ближе к 3, когда x приближается к x=2 слева.

С другой стороны, боковой предел функции при x=2 по линии стоит 6. Потому что если мы приближаемся к точке x=2 по ее линии, функция принимает значения все ближе и ближе к f(x)= 6.

С другой стороны, следует знать, что боковые пределы обладают теми же свойствами, что и обычные пределы. По следующей ссылке вы можете увидеть, каковы свойства границ:

➤ См.: свойства границ.

равные боковые пределы

Мы только что видели пример, где боковые пределы функции различны, но… что произойдет, если боковые пределы одинаковы?

Если оба боковых предела функции в точке существуют и равны , предел функции существует в этой точке, и результатом предела является значение боковых пределов.

Другими словами, чтобы предел функции существовал в точке, должно выполняться следующее условие:

Следовательно, если боковые пределы функции в какой-то точке различны, то предела функции в этой точке не существует.

Кроме того, существование предела функции в точке является существенным условием того, чтобы она была непрерывной функцией в точке .

Давайте решим пример, чтобы завершить понимание концепции боковых ограничений:

Боковые пределы в точке х=-2 функции, представленной графически, совпадают, так как значение функции стремится к 3 независимо от того, приближаемся ли мы к х=-2 слева или справа. Следовательно, предел функции при x=-2 равен 3.

С другой стороны, в точке x=4 боковые пределы другие, так как слева функция приближается к f(x)=3, а справа функция приближается к f(x)=2. Следовательно, предела функции в этой точке не существует.

Расчет боковых пределов

Учитывая определение боковых пределов, мы увидим, как они рассчитываются численно, решив следующий пример:

Если вычислить предел как обычно, мы получим неопределенность действительного числа, разделенного на 0:

Однако при расчете боковых пределов мы не получаем никакой неопределенности.

Чтобы вычислить боковой предел функции слева при x=2, необходимо взять число меньше x=2, но очень близкое к нему, например x=1,999.

В этом случае знаменатель будет отрицательным числом с очень маленьким значением, но даже не нулевым, и обычно обозначается нулем и знаком минус перед ним:

Следовательно, результат бокового предела равен минус бесконечности, поскольку любое число, разделенное на 0, дает бесконечность, а положительное, разделенное на отрицательное, дает отрицательное:

Мы можем убедиться, что функция приближается к минус бесконечности, вычисляя слева изображения функции со значениями ближе к x=2.

Аналогично, чтобы найти предел функции в точке x=2 справа, мы можем применить те же рассуждения: мы берем значение больше 2, но очень близкое, например 2001.

Точно так же мы можем убедиться в стремлении функции к бесконечности, вычисляя справа изображения функции со значениями все ближе и ближе к x=2.

На следующем графике вы можете увидеть анализируемую функцию. Как видите, боковой предел функции в точке x=2 слева равен минус бесконечности, а боковой предел функции в точке x=2 справа равен плюс бесконечности.

Исправлены проблемы с боковыми границами

Упражнение 1

Найдите боковые пределы следующей кусочно определенной функции в точках изменения определения (x=-2 и x=4).

Боковые пределы не совпадают в точке x=-2, слева функция стремится к f(x)=5, а с другой стороны справа функция постоянна и имеет значение 3.

Боковые пределы также различаются по мере того, как x приближается к 4. Кусочная функция приближается к 3 слева, но приближается к -2 справа.

Упражнение 2

Определите, существует ли предел при приближении x к 3 следующей кусочной функции, и если да, то каково его значение.

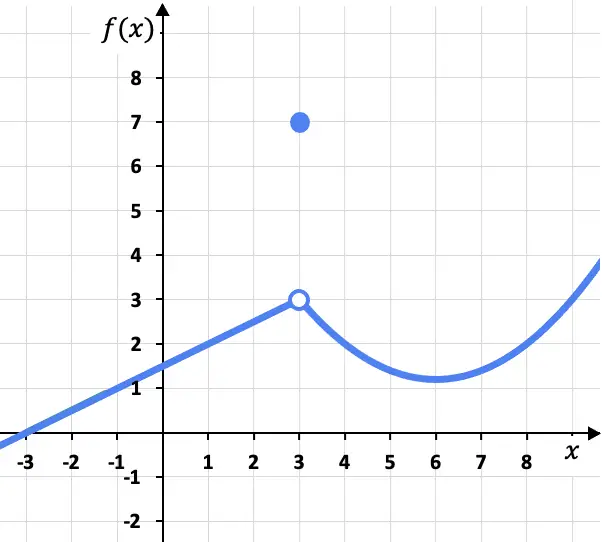
В этой задаче боковые пределы в точке x=3 слева и справа одинаковы, так как функция стремится к одному и тому же значению (f(x)=3) независимо от того, приближаются ли к ней слева или справа. . его правая сторона:

Следовательно, согласно математическому определению предела, предел функции при стремлении х к 3 равен 3, поскольку два боковых предела в этой же точке совпадают при этом значении:

Хотя предел функции при x=3 равен 3, необходимо учитывать, что функция в этой точке равна не 3, а f(3)=7. Как мы увидим позже, это означает, что функция не является непрерывной при x=3, а имеет разрыв, которого можно избежать.

Упражнение 3

Вычислите боковые пределы следующей рациональной функции в точке x=4.

Чтобы вычислить предел, когда x стремится к 4 слева, мы берем значение меньше 4, но очень близкое к нему, например 3999:

Таким образом, боковой предел при приближении x к 4 слева равен плюс бесконечности.

И чтобы решить предел, когда x стремится к 4 справа, мы оцениваем функцию по значению больше 4, но очень близкому к нему, например 4001:

Таким образом, боковой предел при приближении x к 4 справа равен минус бесконечности.

Упражнение 4

Найдите предел, если он существует, следующей кусочной функции, определенной в точке x=2: