В этой статье мы объясним, что такое ограниченные (верхние и нижние) функции. Кроме того, мы покажем вам, что означает ограниченность функции в точке, и, наконец, вы узнаете свойства этого типа функции.
Что такое ограниченная функция?
Ограниченная функция — это функция, график которой находится в определенных пределах. То есть функция ограничена сверху, если существует число K такое, что не существует значения функции, большего, чем K (f(x)≤K), и функция ограничена снизу, если существует число K такое, что оно меньше всех значений функции (f(x)≥K). Следовательно, ограниченная функция — это функция, ограниченная сверху и снизу.
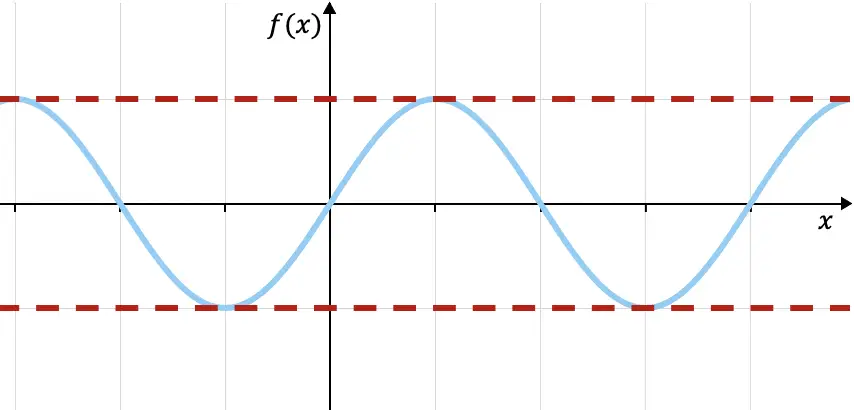
Например, тригонометрическая функция синуса, изображенная на графике выше, ограничена сверху f(x)=1 и ограничена снизу f(x)=-1 (красные пунктирные линии), поскольку все значения функция находится в этих двух пределах. Дополнительные свойства этой функции вы можете увидеть по следующей ссылке:
➤ См.: Характеристики синусоидальной функции.
функция, ограниченная сверху
Однако не все функции ограничены сверху и снизу, функция может быть ограничена только сверху или снизу.
К указанным выше ограниченным функциям относятся те, которые не превышают определенного значения, то есть выполняется следующее условие:
![]()
где значение K является верхней границей функции.
Например, следующая парабола ограничена сверху величиной K=7, но функция не ограничена снизу, поскольку ее ветви простираются до бесконечности.

Логично, что если функция ограничена K=7, она также ограничена K=8 и более высокими значениями.
Наименьшая верхняя граница называется верхней границей и обозначается как sup(f) . Более того, если функция достигает указанного верхнего предела в своей области определения, мы будем говорить, что эта точка является абсолютным максимумом функции.
➤ Смотрите: каковы максимумы и минимумы функции?
В нашем случае функция геометрически ограничена величиной K=7, поэтому это верхний экстремум и абсолютный максимум функции.
функция ограничена ниже
Ниже перечислены функции , которые не имеют значения меньше определенного числа, то есть они удовлетворяют следующему математическому выражению:
![]()
Где значение K является нижней границей функции.
Ниже вы видите графическое представление экспоненциальной функции, которая ограничена ниже K=3:

Очевидно, что функция также ограничена значениями меньше K=3.
Как и прежде, наибольшая нижняя граница называется нижней границей и обозначается inf(f) . Более того, если функция достигает указанного нижнего экстремума в своей области определения, мы будем говорить, что эта точка является абсолютным минимумом функции.
В данном случае K=3 не является абсолютным минимумом функции, поскольку функция достигает этого значения на бесконечности и, следовательно, находится вне своей области определения. Другими словами, f(x)=3 — горизонтальная асимптота функции .
Существует теорема, позволяющая узнать, ограничена ли функция сверху и снизу без ее графического представления. Нажмите здесь, чтобы узнать, что такое теорема Вейерштрасса.
➤ См.: Теорема Вейерштрасса.
Функция, ограниченная в одной точке
Мы только что изучили понятие ограничения функции в целом, но можно также проанализировать, ограничена ли функция в меньшей окрестности, то есть в части функции.
Ага
![]()
является точкой области определения функции и
![]()
любое значение, будем говорить, что функция ограничена сверху/снизу в точке
![]()
если есть окружение
![]()
где функция ограничена сверху/снизу.
Следовательно, функция ограничена в точке
![]()
если он ограничен сверху и снизу в окрестности
![]()
Очевидно, что если функция ограничена вообще, то она будет ограничена и в каждой своей точке. Однако обратное неверно, то есть функция может быть ограничена в каждой из своих точек и не ограничена во всей своей области определения.
Например, следующая аффинная функция частично ограничена в каждой из своих точек, но не является ограниченной функцией.

Свойства ограниченных функций
Ограниченные функции обладают следующими свойствами:
- Ага

И

две ограниченные функции, сложение (или вычитание) двух функций
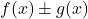
также является ограниченной функцией.
- Ага

И

две ограниченные функции, произведение двух функций
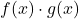
также оказывается ограниченной функцией.
- Если функция имеет вертикальную асимптоту, она не может быть полностью ограничена. С другой стороны, функция может быть ограничена сверху или снизу.
- Любая непрерывная и ограниченная на интервале функция интегрируема.