На этой странице вы найдете все о гиперболическом тангенсе: какова его формула, графическое изображение, все его характеристики…
Формула гиперболического тангенса
Функция гиперболического тангенса является одной из основных гиперболических функций и обозначается символом tanh(x) . Математически гиперболический тангенс равен гиперболическому синусу, разделенному на гиперболический косинус.
![]()
Из формулы гиперболического синуса и формулы гиперболического косинуса можно прийти к следующему выражению:
![]()
Следовательно, функция гиперболического тангенса связана с показательной функцией. По следующей ссылке вы можете увидеть все характеристики этих типов функций:
➤ См.: характеристики показательных функций.
Графическое изображение гиперболического тангенса
Из его формулы мы можем графически представить функцию гиперболического тангенса:
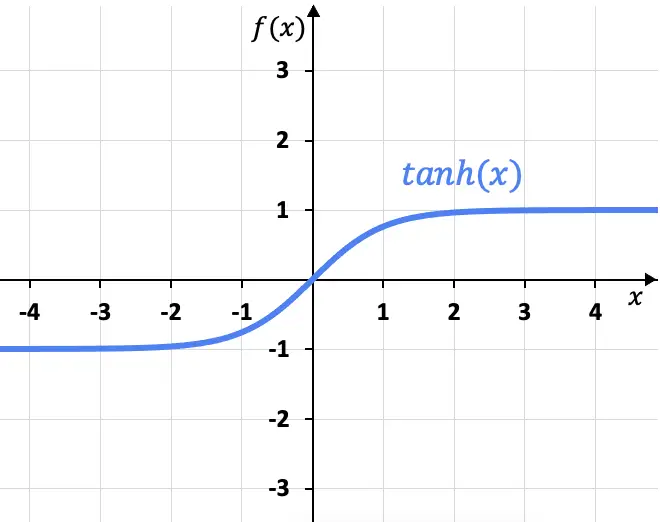
Как видно из графика, функция гиперболического тангенса имеет две горизонтальные асимптоты при x=+1 и x=-1, поскольку предел функции при приближении x к плюс бесконечности дает x=+1, а предел к минус бесконечности. дает х=-1.
С другой стороны, график гиперболического тангенса не имеет ничего общего с графиком тангенса (тригонометрической функции), который является периодической функцией. Графическое представление тангенса и его отличие от гиперболического тангенса вы можете увидеть по следующей ссылке:
➤ См.: графическое представление функции тангенса.
Характеристики гиперболического тангенса
Функция гиперболического тангенса обладает следующими свойствами:
- Областью определения функции гиперболического тангенса являются все действительные числа.
![]()
- Напротив, путь или диапазон функции гиперболического тангенса ограничен значениями от -1 до +1 (не включительно).
![]()
- Гиперболический тангенс — непрерывная, биективная и нечетная функция (симметричная относительно начала координат).
![]()
- Функция пересекает оси X и оси Y в начале координат.
![]()
- Пределы плюс/минус бесконечности функции гиперболического тангенса дают +1/-1. Следовательно, функция имеет горизонтальную асимптоту при x=+1 и еще одну горизонтальную асимптоту при x=-1.
![]()
![]()
- Гиперболический тангенс строго возрастает во всей своей области, поэтому он не имеет относительных экстремумов (ни максимума, ни минимума).
- Однако в точке x = 0 функция меняется с выпуклой на вогнутую, поэтому x = 0 является точкой перегиба функции.
- Обратная функция гиперболического тангенса называется аргументом гиперболического тангенса (или гиперболического арктангенса), и его формула выглядит следующим образом:
![]()
- Производная функции гиперболического тангенса равна 1, деленной на квадрат гиперболического косинуса:
![]()
- Интеграл от функции гиперболического тангенса представляет собой натуральный логарифм гиперболического косинуса:
![]()
- Гиперболический тангенс суммы двух разных чисел можно вычислить, применив следующее уравнение:
![]()
- Полином Тейлора или гиперболический касательный ряд имеет радиус сходимости
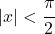
и соответствует следующему выражению:
![]()
Золото
![]()
это число Бернулли .