Гиперболическая функция синуса

В этой статье вы найдете все о гиперболическом синусе: какова его формула, графическое изображение, все его характеристики, связи с другими функциями…

Формула гиперболического синуса

Гиперболический синус является одной из основных гиперболических функций и обозначается символом sinh(x) или sinh(x) . Гиперболический синус равен ex ^минус e ^-x , деленный на 2.

Таким образом, формула гиперболического синуса выглядит следующим образом:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

Таким образом, гиперболический синус связан с показательной функцией.

➤ См.: характеристики показательной функции

Графическое изображение гиперболического синуса

Используя формулу, которую мы видели в предыдущем разделе, мы можем составить таблицу значений гиперболического синуса и построить график функции:

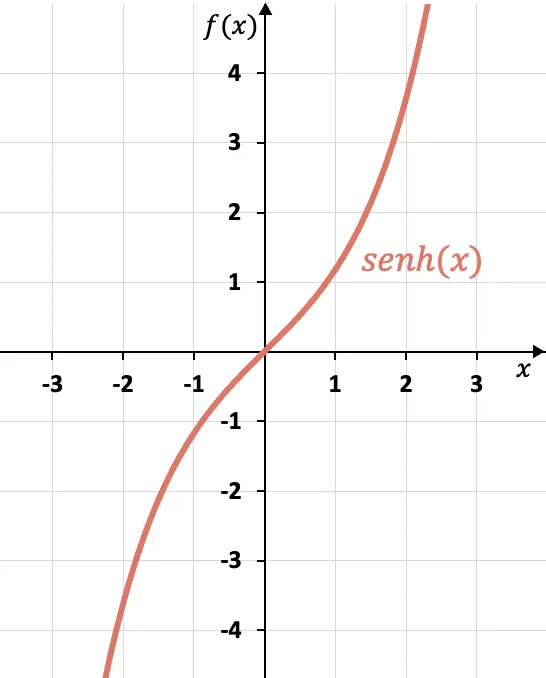
На этом графике мы видим, что гиперболический синус является нечетной функцией, потому что противоположные x имеют противоположные образы, или, другими словами, график гиперболического синуса симметричен относительно начала координат (0, 0).

Как видите, график гиперболического синуса сильно отличается от графика синуса, который является периодической функцией. Графическое представление синуса и все отличия от гиперболического синуса вы можете увидеть по следующей ссылке:

➤ См.: Графическое представление синусоидальной функции.

Характеристики гиперболического синуса

Гиперболический синус обладает следующими свойствами:

Областью определения функции гиперболического синуса являются все действительные числа:

$\text{Dom } f = \mathbb{R}$

Диапазон или диапазон функции гиперболического синуса также являются действительными числами.

$\text{Im } f= \mathbb{R}$

Гиперболический синус — непрерывная и нечетная функция.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Перехватывает оси X и оси Y в одной и той же точке пересечения, начале координат:

$(0,0)$

Предел гиперболической синусоидальной функции при стремлении x к плюс/минус бесконечности равен плюс/минус бесконечности:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

Гиперболический синус строго возрастает во всей области, поэтому не имеет ни максимумов, ни минимумов.

Однако она меняет свою кривизну в точке x = 0, поэтому это точка перегиба функции. Для значений меньше x=0 это вогнутая функция, а для значений больше x=0 это выпуклая функция.

Производной функции гиперболического синуса является гиперболический косинус:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Точно так же интеграл от гиперболического синуса представляет собой гиперболический косинус:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

Ряд Тейлора гиперболической синусоидальной функции эквивалентен следующему выражению:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

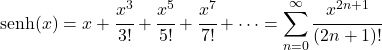
Преобразование Лапласа гиперболической синусоидальной функции выглядит следующим образом:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Математические отношения гиперболического синуса

Гиперболический синус связан с другими гиперболическими функциями следующими уравнениями:

Фундаментальное уравнение связывает гиперболический синус с гиперболическим косинусом:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Следовательно, гиперболические функции синус и косинус связаны уравнением гиперболы, которое имеет вид x ² -y ² =1. В отличие от тригонометрических функций синуса и косинуса, которые связаны уравнением окружности (x ² +y ² =1).

Гиперболические функции синуса, косинуса и тангенса могут быть связаны следующим уравнением:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

С другой стороны, гиперболический синус сложения или вычитания двух разных чисел можно рассчитать по следующим формулам:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

Гиперболический синус удвоенного числа можно определить, применив следующее математическое соотношение:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

Сумму или вычитание двух гиперболических синусов можно найти по следующим формулам:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Наконец, квадрат гиперболического синуса можно вычислить, применив следующую формулу:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Гиперболическая синусоидальная функция

Формула гиперболического синуса

Графическое изображение гиперболического синуса

Характеристики гиперболического синуса

Математические отношения гиперболического синуса

Оставьте комментарий Отменить ответ