На этой странице вы найдете все о функции тангенса: что это такое, какова ее формула, как ее представить на графике, характеристики функции, ее период и т.д. Кроме того, вы сможете увидеть примеры касательных функций, чтобы полностью понять концепцию. Он даже объясняет теорему о касательной и связи, которые имеет касательная функция с другими тригонометрическими соотношениями.
Формула касательной функции
Касательная функция угла α — это тригонометрическая функция, формула которой определяется как отношение противоположной ветви к смежной (или смежной) ветви прямоугольного треугольника (треугольника с прямым углом).

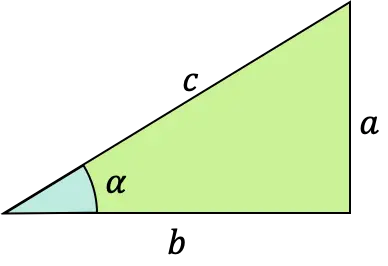
Этот тип математической функции также называется тангенциальной, тангеноидной или тангенциальной функцией. И это можно выразить аббревиатурой «тг» или даже «тан».
Функция тангенса — одно из трёх самых известных тригонометрических отношений, наряду с синусом и косинусом угла.
Характеристические значения функции тангенса
Существуют определенные углы, которые часто повторяются, поэтому удобно знать значение функции тангенса при этих углах:
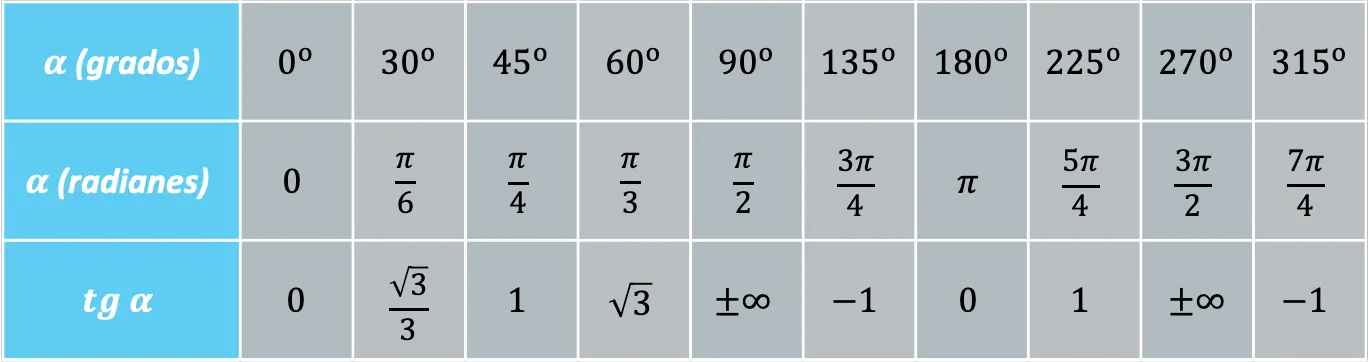
С другой стороны, функция тангенса может быть связана с функциями синуса и косинуса следующим фундаментальным тригонометрическим тождеством:
![]()
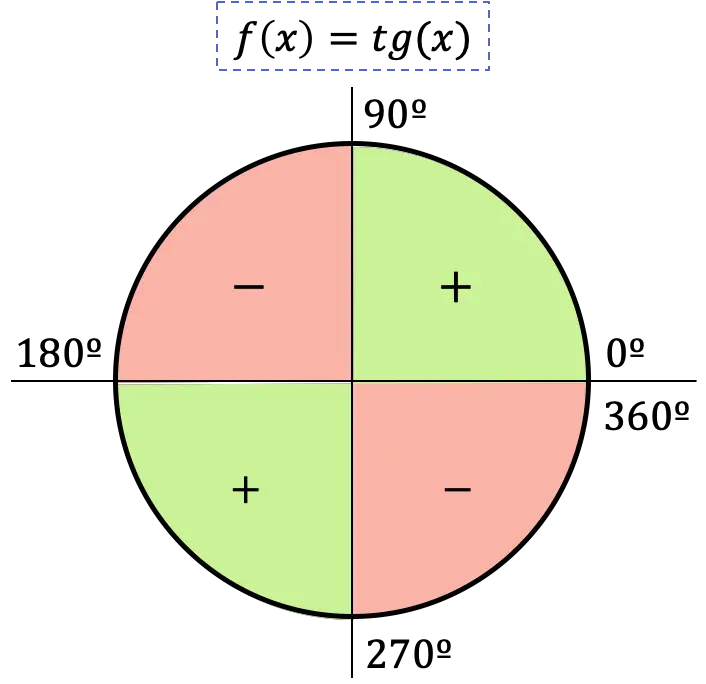
Таким образом, знак касательной функции зависит от квадранта, в котором находится угол:
- Если угол принадлежит первой четверти, то ее тангенс будет положительным, так как в этой четверти синус и косинус также положительны.
- Если угол попадает во вторую четверть, то ее тангенс будет отрицательным, поскольку в этой четверти синус положителен, а косинус отрицателен.
- Если угол находится в третьем квадранте, его тангенс будет положительным, поскольку в этом квадранте синус и косинус отрицательны.
- Если угол находится в четвертом квадранте, его тангенс будет отрицательным, так как в этом квадранте синус отрицателен, а косинус положителен.
Графическое представление функции тангенса
С помощью таблицы значений, которую мы видели в предыдущем разделе, мы можем построить график функции тангенса. Построив график функции тангенса, мы получим:
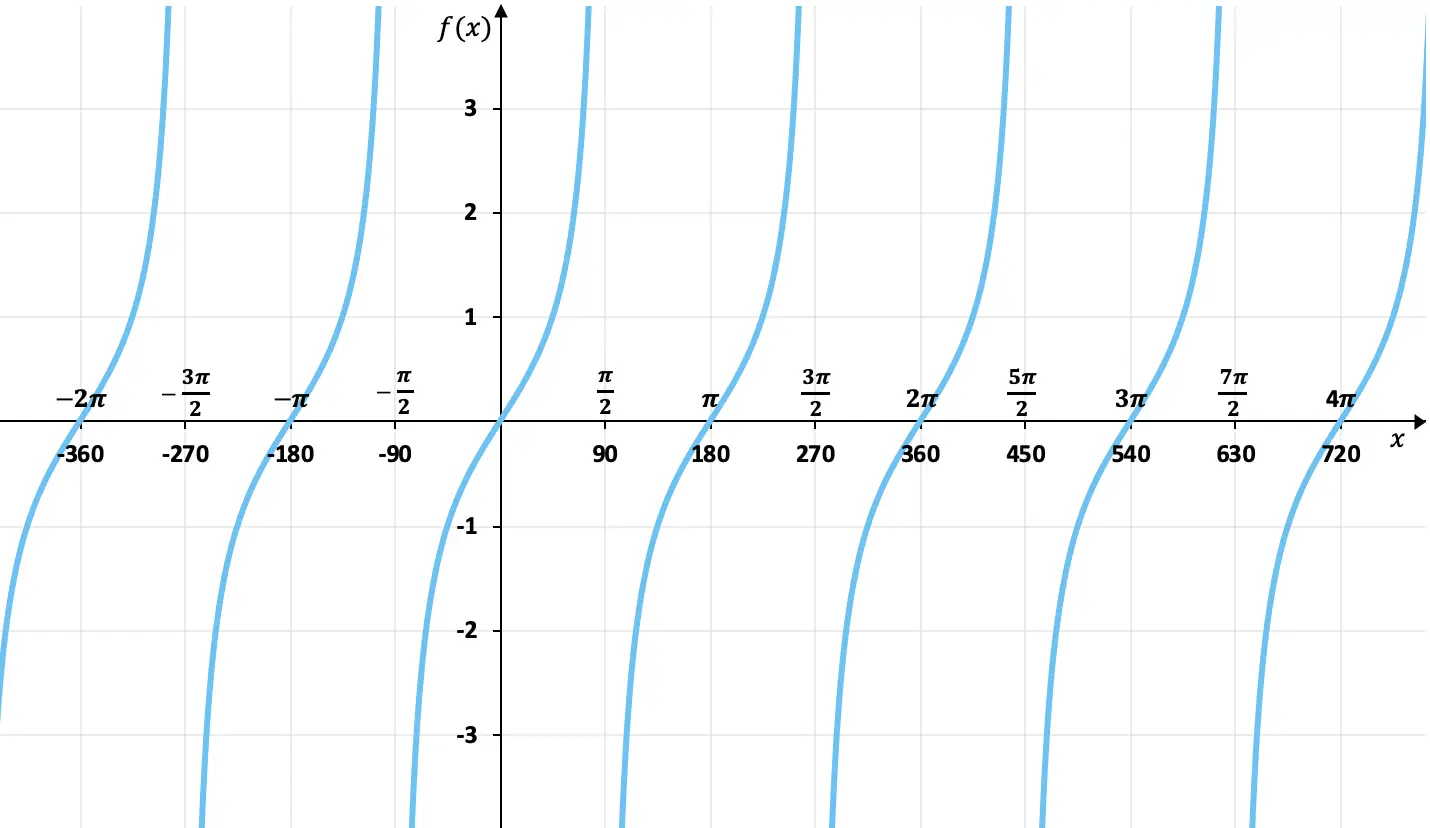
Как видно из графика, значения изображений функции тангенса не ограничены, в отличие от функций синуса и косинуса. Кроме того, значения повторяются каждые 180 градусов (π радиан), поэтому это периодическая функция , период которой равен 180º.
С другой стороны, на этом графике мы видим, что касательная функция нечетна , поскольку ее противоположные элементы имеют противоположные изображения, или, другими словами, она симметрична относительно начала координат (0,0). Например, тангенс 45° равен 1, а тангенс -45° равен -1.
Наконец, мы также можем видеть, что функция тангенса имеет вертикальные асимптоты . Например, он подходит очень близко к линии x=90º, но никогда не касается ее, и то же самое происходит каждые 180 градусов. Это означает, что предел функции в этих точках стремится к бесконечности.
Свойства касательной функции
Касательная функция имеет следующие характеристики:
- Областью определения функции тангенса являются все действительные числа, кроме точек, в которых существует вертикальная асимптота:
![]()
![]()
- Диапазон или диапазон функции тангенса — это все действительные числа.
![]()
- Это непрерывная и нечетная функция с периодичностью π.
![]()
- Этот тип тригонометрической функции имеет единственную точку пересечения с осью y (ось Y) в точке (0,0).
![]()
- Вместо этого он периодически пересекает абсциссу (ось X) в нескольких координатах числа Пи.
![]()
- Функция строго возрастает во всей области определения, поэтому не имеет ни максимума, ни минимума.
- Производная тангенса:
![]()
- Наконец, интеграл от касательной функции равен:
![]()
Период касательной функции
В отличие от других тригонометрических функций, таких как синус и косинус, функция тангенса не имеет величины, поскольку не имеет ни максимального, ни минимального значения. Однако это периодическая функция, то есть ее значения повторяются с частотой, как мы видели на ее графике.
![]()
- Период касательной функции — это расстояние между двумя точками, в которых график повторяется, и рассчитывается по следующей формуле:
![]()
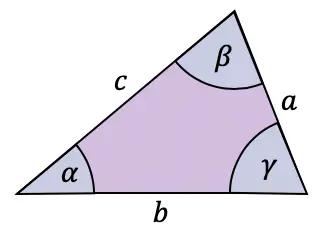
теорема о касательной
Хотя формула касательной обычно используется в прямоугольных треугольниках, существует также теорема, применимая к любому типу треугольников: теорема о касательной.
Теорема о касательной связывает стороны и углы любого треугольника следующим образом:
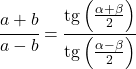
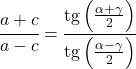
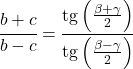
Связь функции тангенса с другими тригонометрическими отношениями
Ниже приведены связи тангенса с наиболее важными тригонометрическими соотношениями тригонометрии.
Отношения с грудью
- Тангенс и синус угла связаны следующим образом:
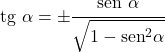
Косинусное соотношение
- Аналогично тангенс и косинус угла связаны следующим равенством:
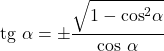
Связь с косекансом
- Хотя это и трудно доказать, тангенс можно решить так, чтобы он зависел только от косеканса:
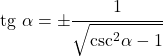
Отношения с секансом
- Тангенс и секанс угла связаны следующим уравнением:
![]()
Связь с котангенсом
- Тангенс и котангенс являются мультипликативными обратными числами:
![]()