Нильпотентная матрица

На этой странице вы найдете объяснение того, что такое нильпотентная матрица, а также несколько примеров, чтобы вы могли в этом разобраться и не сомневаться. Кроме того, вы сможете увидеть структуры нильпотентных матриц и все свойства этих типов матриц.

Что такое нильпотентная матрица?

Определение нильпотентной матрицы следующее:

Нильпотентная матрица — это квадратная матрица, возведенная в целое число и дающая нулевую матрицу .

$N^k =0$

Золото

$N$

является нильпотентной матрицей и

$k$

показатель степени, дающий нулевую матрицу.

Это условие не означает, что степень нильпотентной матрицы всегда дает ноль независимо от показателя степени, а означает, что если существует хотя бы одна степень матрицы, результатом которой является матрица, полная нулей, то матрица нильпотентна.

С другой стороны, индекс нильпотентности нильпотентной матрицы — это наименьшее число, при котором выполняется условие нильпотентности. Также можно сказать, что нильпотентная матрица имеет порядок k , где k — ее индекс нильпотентности.

Примеры нильпотентных матриц

Чтобы завершить понимание концепции нильпотентной матрицы, мы увидим несколько примеров матриц этого типа:

Пример нильпотентной матрицы 2 × 2

Следующая квадратная матрица размерности 2×2 нильпотентна:

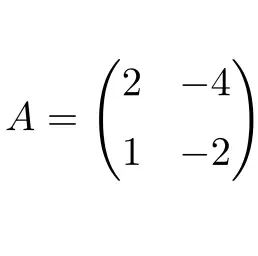
пример нильпотентной матрицы размерности 2x2

Матрица нильпотентна, поскольку, возведя матрицу А в квадрат, мы в результате получим нулевую матрицу:

$\displaystyle A^2=\begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}\cdot \begin{pmatrix} 2 &-4 \\[1.1ex] 1 & -2 \end{pmatrix}=\begin{pmatrix} \bm{0} &\bm{0} \\[1.1ex] \bm{0} & \bm{0} \end{pmatrix}$

Следовательно, это нильпотентная матрица и ее индекс нильпотентности равен 2, поскольку нулевая матрица получается во второй степени.

Пример нильпотентной матрицы 3×3

Следующая квадратная матрица третьего порядка нильпотентна:

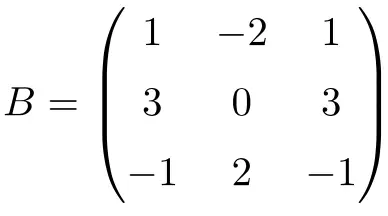
пример нильпотентной матрицы размерности 3x3

Хотя, повышая матрицу до 2, мы не получаем нулевую матрицу:

$\displaystyle B^2=\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}\cdot \begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}$

Но при вычислении куба матрицы мы получаем матрицу, все элементы которой равны 0:

$\displaystyle B^3= \begin{pmatrix}-6&0&-6\\[1.1ex]0&0&0\\[1.1ex] 6&0&6\end{pmatrix}\cdot\begin{pmatrix}1&-2&1\\[1.1ex] 3&0&3\\[1.1ex] -1&2&-1\end{pmatrix}= \begin{pmatrix}\bm{0}&\bm{0}&\bm{0}\\[1.1ex]\bm{0}&\bm{0}&\bm{0}\\[1.1ex] \bm{0}&\bm{0}&\bm{0}\end{pmatrix}$

Итак, матрица B является нильпотентной матрицей, а поскольку нулевая матрица получается в степени 3, то ее индекс нильпотентности равен 3.

Структура нильпотентной матрицы 2 × 2

Ниже вы можете увидеть структуру всех нильпотентных матриц. Его доказательство немного утомительно, поэтому мы предоставили вам непосредственно формулу для получения нильпотентной матрицы второго порядка:

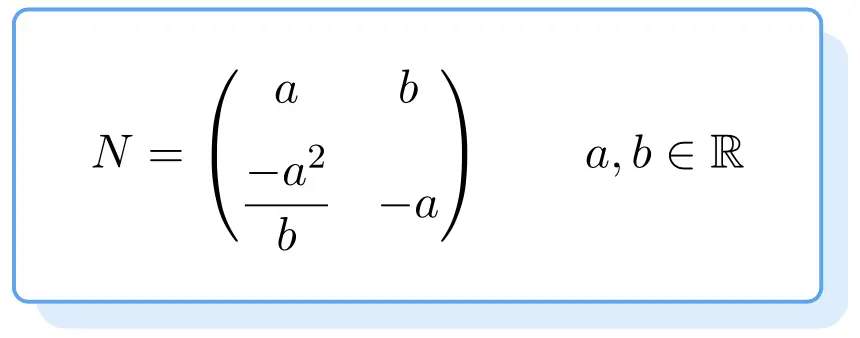
структура и формула нильпотентной матрицы 2x2

Таким образом, любая матрица, удовлетворяющая приведенной выше формуле, будет нильпотентной. Для этого значения

$a$

$b$

они могут быть произвольными, если они являются действительными числами.

Свойства нильпотентных матриц.

Нильпотентные матрицы обладают следующими характеристиками:

След нильпотентной матрицы всегда равен нулю.

Аналогично, определитель любой нильпотентной матрицы всегда равен 0. Однако обратное неверно, т.е. нулевой определитель матрицы не означает, что матрица нильпотентна.

Единственная нильпотентная матрица, которую можно диагонализовать, — это нулевая матрица.

Индекс нильпотентности нильпотентной матрицы размерности n×n всегда равен или меньше n . Вот почему индекс нильпотентности нильпотентной матрицы размера 2 × 2 всегда будет равен 2.

Нильпотентная матрица не является обратимой.

Любая треугольная матрица с нулями на главной диагонали также является нильпотентной.

Существует теорема, которая гласит, что если матрица
$N$

нильпотентна, то матрица

$N+I$

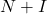
обратима, где

$I$

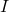
является единичной матрицей. Кроме того, его обратную матрицу можно найти по следующей формуле:

$\displaystyle(N+I)^{-1} = \sum_{m = 0}^\infty (-N)^m=I-N+N^2-N^3+\cdots$

Эквивалентно, если
$N$

является нильпотентной матрицей, то можно вычислить обратную матрицу

$N-I$

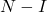
со следующим уравнением:

$\displaystyle(N-I)^{-1} = \sum_{m = 0}^\infty (N)^m=I+N+N^2+N^3+\cdots$

Любую сингулярную матрицу, то есть необратимую, можно разложить в произведение нильпотентных матриц.

Все собственные значения (или собственные значения) нильпотентной матрицы равны нулю.

$\displaystyle \lambda=0 \qquad \forall \ \lambda$

Наконец, как любопытство, существует также концепция нильпотентного преобразования, которая определяет линейное приложение.
$L$

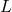
векторного пространства такого, что

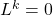
$L^k=0$

.